Riyaziyyatda bir çox anlayış gündəlik həyatımızda qarşımıza çıxmasa da, onların tətbiq sahəsi olduqca genişdir. Məsələn, tortu bərabər hissələrə bölmək, su borularını eyni uzunluqlarla kəsmək, proqramlaşdırmada sadələşdirilmiş hesablamalar aparmaq və ya ən kiçik vahidlərlə işləmək – bütün bu məsələlərdə ƏBOB (Ən Böyük Ortaq Bölən) anlayışı vacib rol oynayır.
ƏBOB sadə səslənsə də, arxasında ciddi riyazi məntiq və tətbiqlər dayanır. Bu məqalədə əbob nədir, necə tapılır, hansı düsturlarla hesablamaq mümkündür və Python proqramlaşdırma dilində tətbiqi ilə bağlı dərin, informativ və hər kəsin başa düşəcəyi şəkildə yazılmış məlumatlar təqdim edirik.
ƏBOB nədir?
ƏBOB – “Ən Böyük Ortaq Bölən” sözlərinin qısaltmasıdır. İki və ya daha çox ədədin ortaq bölənlərinin içində ən böyüyünü ifadə edir.
Sadə dillə desək:
Əgər iki ədədin hər ikisini bölən bir neçə ədəd varsa və bu ədədlərdən ən böyüyünü tapmaq istəyiriksə, bu ƏBOB olur.
Məsələn:
Əgər ədədlərimiz 18 və 24-dürsə:
- 18-in bölənləri: 1, 2, 3, 6, 9, 18
- 24-ün bölənləri: 1, 2, 3, 4, 6, 8, 12, 24
Bu ədədlərin ortaq bölənləri: 1, 2, 3, 6
Ən böyüyü isə 6-dır.
Deməli, ƏBOB(18, 24) = 6
ƏBOB-un gündəlik həyatda tətbiqləri
ƏBOB yalnız riyaziyyat dərslərində deyil, real həyatda da faydalı ola bilər:
- Qalan məhsulları bərabər hissələrə bölmək: Məsələn, 36 alma və 60 portağalı bərabər səbətlərə bölmək istəyirsinizsə, ƏBOB sizə maksimum neçə səbət lazım olduğunu göstərə bilər.
- Riyazi sadələşdirmə: Ədədlərin sadələşdirilməsi üçün istifadə olunur.
- Zaman və dövrlərin uyğunlaşdırılması: Məsələn, 3 və 4 dəqiqədən bir işləyən iki cihazın eyni anda işə düşməsini analiz etməkdə istifadə edilir.
- Kriptoqrafiya və riyazi proqramlaşdırmada: ƏBOB alqoritmlər üçün vacibdir.
ƏBOB tapma yolları və düsturları
ƏBOB tapmağın bir neçə üsulu var. Aşağıda ən çox istifadə olunan metodları təqdim edirik:
1. Sadə bölənlərlə tapma (Ənənəvi üsul)
- Hər iki ədədin bölənlərini tapın
- Ortax bölənləri müəyyən edin
- Onların ən böyüyünü seçin
Misal: ƏBOB(12, 30)
- 12: 1, 2, 3, 4, 6, 12
- 30: 1, 2, 3, 5, 6, 10, 15, 30
Ortaq: 1, 2, 3, 6 → ƏBOB = 6
2. Evklid Alqoritmi
Evklid alqoritmi ƏBOB-un tapılmasında ən səmərəli üsullardan biridir. Prinsipi sadədir:
ƏBOB(a, b) = ƏBOB(b, a mod b)
Mod – bölmədən qalan hissədir.
Misal: ƏBOB(48, 18)
- 48 % 18 = 12
- ƏBOB(18, 12)
- 18 % 12 = 6
- ƏBOB(12, 6)
- 12 % 6 = 0 → deməli, ƏBOB = 6
3. Sadə vuruqlara ayıraraq
Hər iki ədədin sadə vuruqlara ayrılması yolu ilə ortaq vuruqları müəyyən edirik.
Misal:
- 36 = 2² × 3²
- 60 = 2² × 3 × 5
Ortaq vuruqlar: 2² × 3 = 12
ƏBOB(36, 60) = 12
ƏBOB və ƏKOB (Ən Kiçik Ortaq Vahid) əlaqəsi
Riyaziyyatda maraqlı bir əlaqə var:
ƏBOB(a, b) × ƏKOB(a, b) = a × b
Bu düstur, iki ədədin ortaq böləni və ortaq hasilini bir-biri ilə əlaqələndirir.
Bu üsulla birini bilib o birini hesablamaq mümkündür.
Python proqramlaşdırma dilində ƏBOB tapmaq
ƏBOB-un proqramlaşdırılması Python dilində olduqca rahatdır. Aşağıda həm manual, həm də hazır math modulundan istifadə edən iki üsul təqdim olunur:
1. Evklid üsulu ilə özümüz yazdığımız funksiya:
pythonCopyEditdef ebob(a, b):
while b != 0:
a, b = b, a % b
return a
print(ebob(36, 60)) # Nəticə: 12
2. Python math modulundan istifadə:
pythonCopyEditimport math
print(math.gcd(36, 60)) # Nəticə: 12
Bu funksiyadan həm iki, həm də çoxsaylı ədədlər üçün istifadə etmək mümkündür.
ƏBOB-un çoxsaylı ədədlər üçün hesablanması
Əgər 3 və ya daha çox ədədin ƏBOB-u tapılmalıdırsa, mərhələli şəkildə hesablamaq lazımdır:
Misal: ƏBOB(24, 36, 60)
- ƏBOB(24, 36) = 12
- ƏBOB(12, 60) = 12
Nəticə: 12
Python ilə:
pythonCopyEditfrom math import gcd
from functools import reduce
def ebob_list(numbers):
return reduce(gcd, numbers)
print(ebob_list([24, 36, 60])) # Nəticə: 12
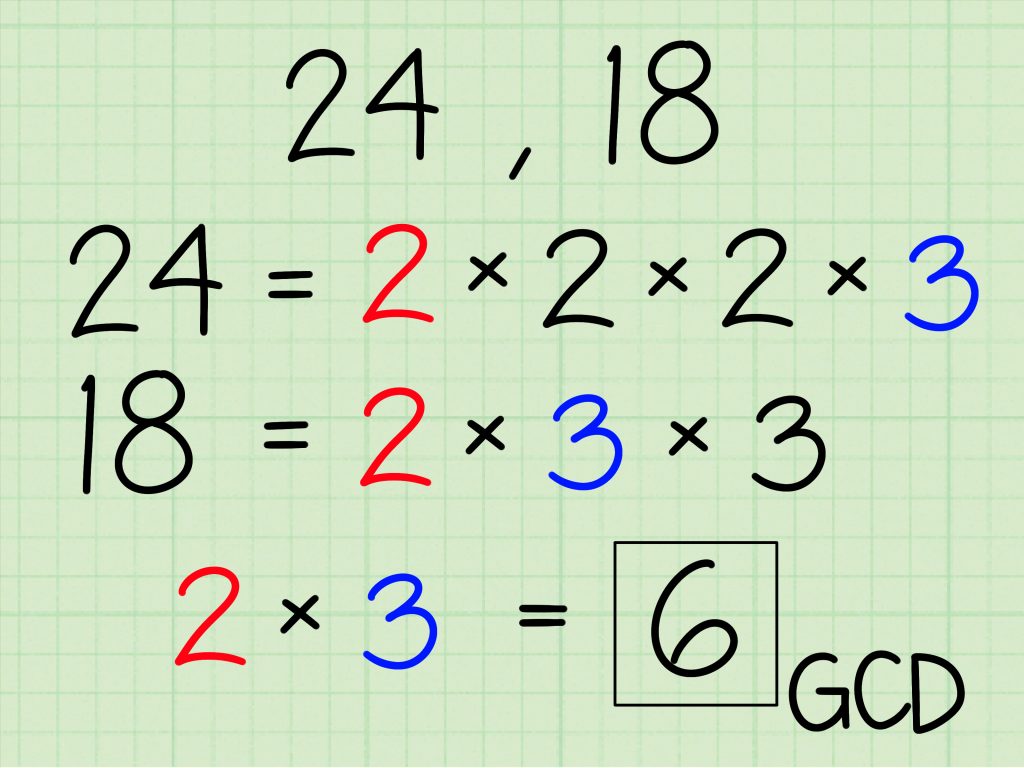
ƏBOB haqqında tez-tez verilən suallar
1. ƏBOB mənfi ədədlərlə necə işləyir?
ƏBOB yalnız müsbət ədədlərlə hesablanır. Mənfi ədədlər varsa, onların müsbət qarşılığı götürülür.
2. Əgər iki ədədin ortaq böləni yoxdursa, ƏBOB nə olur?
Əgər ortaq bölən yalnız 1-dirsə, ƏBOB = 1. Bu cür ədədlərə “nəticəsiz” deyil, “qarşılıqlı sadə” deyilir.
3. ƏBOB ilə ƏKOB-un fərqi nədir?
ƏBOB – bölənlərin ən böyüyüdür,
ƏKOB – ortaq hasilin ən kiçiyidir.
ƏBOB yalnız riyaziyyat kitablarında qalmayan, gündəlik həyatda da istifadə oluna biləcək dəyərli bir anlayışdır. Onun düsturları sadədir, tətbiqi genişdir, xüsusilə proqramlaşdırmada və sadə məntiqdə tez-tez rast gəlinir.
Python proqramlaşdırma dilində ƏBOB-un tapılması həm öyrədici, həm də praktik bacarıqdır. Bu mövzu məktəblilər, tələbələr, müəllimlər, proqramçılar və ümumilikdə hər kəs üçün faydalı ola bilər.