Riyaziyyat aləminin əsas sütunlarından biri olan çoxluqlar anlayışı həm gündəlik həyatda, həm məntiqdə, həm də ali riyaziyyatda geniş tətbiq sahəsinə malikdir. Çoxluqlar nəzəriyyəsi riyazi düşüncənin formalaşmasında mühüm rol oynayır.
Çoxluq nədir?
Riyaziyyatda çoxluq müəyyən obyektlərin və ya elementlərin toplandığı bir anlayışdır. Bu obyektlər canlı və cansız, ədədi və ya həndəsi, anlayış və ya simvol ola bilər. Məsələn, A = {1, 2, 3} çoxluğu 1, 2 və 3 ədədlərindən ibarət olan bir çoxluqdur. Bu elementlər bir-birindən fərqlidir və qeyri-nizamlı düzülüşə malikdir – yəni {1, 2, 3} ilə {3, 2, 1} eyni çoxluq sayılır.
Çoxluqların işarələri və terminlər
Çoxluqlar riyaziyyatda müxtəlif işarələrlə göstərilir:
- ∈ – “daxildir” işarəsi. Məsələn, 2 ∈ A – 2 elementi A çoxluğuna daxildir.
- ∉ – “daxil deyil” işarəsi. Məsələn, 4 ∉ A
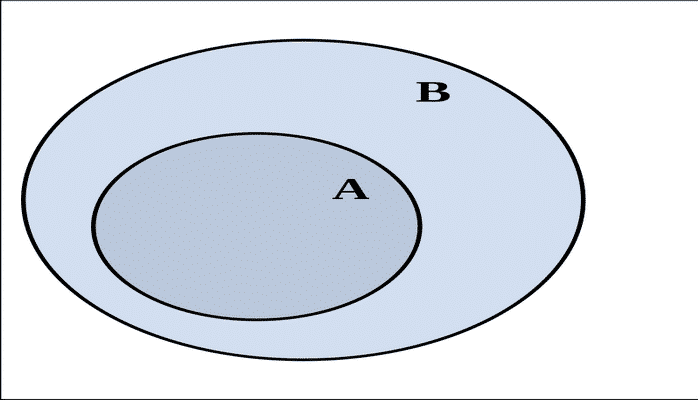
- ⊂ – “alt çoxluq” işarəsi. Məsələn, B ⊂ A o deməkdir ki, B çoxluğunun bütün elementləri A-ya daxildir.
- ∪ – birləşmə
- ∩ – kəsişmə
- \ – fərq
Çoxluqlar üzərində əsas əməllər
1. Çoxluqların birləşməsi (A ∪ B) Hər iki çoxluqda olan bütün elementlər birləşdirilir. Misal: A = {1, 2, 3} B = {3, 4, 5} A ∪ B = {1, 2, 3, 4, 5}
2. Çoxluqların kəsişməsi (A ∩ B) Hər iki çoxluqda eyni anda olan elementlər seçilir. Misal: A = {1, 2, 3} B = {3, 4, 5} A ∩ B = {3}
3. Çoxluqların fərqi (A \ B) A-da olub, B-də olmayan elementlərdən ibarət çoxluq. Misal: A = {1, 2, 3} B = {3, 4, 5} A \ B = {1, 2}
4. Dekart hasili (A × B) A və B çoxluqlarının bütün mümkün cütlükləri: Misal: A = {1, 2} B = {a, b} A × B = {(1, a), (1, b), (2, a), (2, b)}
Çoxluqlar nəzəriyyəsinin əsasları və tətbiqləri
Çoxluqlar nəzəriyyəsi riyaziyyatın digər sahələrinin – məntiqin, funksiyaların, ehtimal nəzəriyyəsinin təməlidir. Məktəb proqramlarında bu mövzu 6-7-ci siniflərdən başlayaraq öyrədilir. Lakin universitet səviyyəsində də çoxluqlar daha dərin şəkildə təhlil olunur. Kompüter elmləri, verilənlər bazası, proqramlaşdırma dillərində (məsələn, Python, SQL) çoxluqlar anlayışından istifadə olunur.
Çoxluqlar test və sınaq materialları
Şagirdlərin və tələbələrin çoxluqları daha yaxşı mənimsəməsi üçün testlər və PDF sınaqlar mövcuddur. Bu materiallar adətən:
- Düzgün işarə istifadəsi
- Birləşmə, kəsişmə, fərq əməliyyatı
- Alt çoxluqların sayı və hesablanması
- Venn diaqramları üzərində tapşırıqlardan ibarət olur.
“Çoxluqlar test PDF”, “çoxluqlar sınaq” kimi açar sözlərlə onlayn axtarış etdikdə riyaziyyat müəllimləri və tədris mərkəzləri tərəfindən hazırlanmış çox sayda material tapmaq mümkündür.
Çoxluqların düsturları
Bəzi vacib düsturlar:
- |A ∪ B| = |A| + |B| – |A ∩ B| – birləşmənin gücü
- 2^n – n elementli çoxluğun alt çoxluqlarının sayı
- Boş çoxluq – heç bir elementi olmayan çoxluq, ∅ ilə işarə olunur
- Əsas çoxluq – bütün digər çoxluqların daxil olduğu ümumi çoxluq (U ilə işarə olunur)
Venn diaqramları və vizual təhlil
Çoxluqların təsvirində Venn diaqramları mühüm rol oynayır. Bu diaqramlar çevrələrlə təmsil olunan çoxluqları və onların qarşılıqlı əlaqələrini vizual şəkildə göstərir. Xüsusilə kəsişmə və birləşmə əməliyyatlarında bu diaqramlar anlayışı asanlaşdırır.
Çoxluqların tarixi və yaranması
- Çoxluqlar nəzəriyyəsinin əsasını XIX əsrdə alman riyaziyyatçısı Georg Cantor qoymuşdur.
- Cantor ilk dəfə sonsuz çoxluqları və onların müqayisəsini tədqiq etmişdir.
- Onun fikirləri əvvəlcə ciddi mübahisələr doğursa da, sonradan riyaziyyatın əsas sütunlarından birinə çevrilmişdir.
- Bu nəzəriyyə funksiyalar, ardıcıllıqlar və hətta kompüter elmlərinin əsasını təşkil edir.
Sonsuz çoxluqlar və maraqlı faktlar
- Sonsuz çoxluqlar “sayılabilən” və “sayılmayan” olaraq iki yerə bölünür.
- Məsələn, təbii ədədlər çoxluğu sayılabiləndir, real ədədlər isə sayılmayan.
- Bu, riyaziyyatdakı ən dərin və maraqlı paradokslardan biridir.
Çoxluqlar və gündəlik həyat
- Məsələn, “sarı rəngli meyvələr” və “turş meyvələr” iki çoxluq kimi qəbul edilə bilər.
- Ərzaq siyahısı, dərs cədvəli, dost siyahısı və ya paltaryuyan rejimləri – hamısı çoxluq kimi təsəvvür edilə bilər.
- Marketdə endirimdə olan məhsullarla evdə lazım olan məhsulların kəsişməsi: bu da çoxluqların gündəlik tətbiqinə misaldır.
Çoxluqlar və proqramlaşdırma
- “Set” anlayışı Python, JavaScript və digər dillərdə çox geniş istifadə olunur.
- Eyni elementlərin avtomatik təkrarlanmaması, kəsişmə, birləşmə funksiyaları kodlaşdırmada vacib rol oynayır.
Çoxluqların məktəb və imtahan sistemində rolu
- Dövlət imtahan mərkəzinin (DİM) testlərində çoxluqlar bölməsi 7-ci və 9-cu siniflərdə, həmçinin qəbul imtahanlarında yer alır.
- İxtisas imtahanlarında və müəllimlərin diaqnostik qiymətləndirilməsində bu mövzuya dair suallar tez-tez verilir.
- Mövzuya dair əyani və interaktiv metodlarla tədris daha effektiv olur.
Çoxluqlar PDF və onlayn resurslar
Çoxluqlar mövzusunu öyrənmək üçün PDF sənədlər, dərsliklər və interaktiv resurslar olduqca faydalıdır. Bunlara aşağıdakılar daxildir:
- Dövlət imtahan mərkəzinin sınaq tapşırıqları
- Müəllimlərin hazırladığı PDF konspektlər
- Online tədris platformaları (Khan Academy, Coursera, və s.)
- Youtube üzərində çoxluqlar dərsləri
Çoxluqlar riyaziyyatın əsas anlayışlarından biri olmaqla yanaşı, məntiqi düşünmənin formalaşmasında və problemlərin strukturlaşdırılmış şəkildə həllində böyük rol oynayır. Onların birləşməsi, kəsişməsi, fərqi və digər əməlləri real həyatda da tətbiq olunur – məsələn, siniflərdə şagird siyahılarında, seçimlərdə və analizlərdə. Bu səbəbdən, çoxluqlar anlayışının yaxşı qavranılması həm şagirdlər, həm müəllimlər, həm də riyazi düşüncəyə sahib olmaq istəyən hər kəs üçün vacibdir.