Riyaziyyat elmində elə sahələr var ki, onların əsas prinsipləri və tətbiqi üsulları insan həyatının hər bir sahəsində, hətta gündəlik reallıqlarımızda da hiss olunur. Triqonometriya da bu sahələrdən biridir. Onun kökləri bəşər sivilizasiyasının formalaşması ilə, qədim Misir, Babil və Hindistan riyaziyyat məktəblərinin təşəkkül dövrü ilə bağlıdır. Qədim astronomlar ulduzların mövqeyini təyin etmək, binalar inşa edənlər dəqiqliklə bucaq ölçmələri aparmaq üçün təbiətin sirrini riyazi şəkildə anlamağa çalışıblar. Triqonometriyanın əsası, əsasən, bucaqlar və onların xassələrinin öyrənilməsinə, bucaqlar arasında funksional əlaqələrin araşdırılmasına söykənir.
Triqonometriya yalnız riyaziyyatçılar üçün yox, mühəndislər, memarlar, fizika, coğrafiya, astronomiya və bir çox başqa sahələrin mütəxəssisləri üçün də əvəzolunmaz elmi baza təşkil edir. Hər bir böyük infrastruktur layihəsi, təyyarə və gəmi naviqasiyası, peyk rabitəsi, hətta mobil texnologiyaların inkişafı triqonometriyanın əsaslarına istinad edir. Gündəlik həyatda isə triqonometriya, bir çoxlarının düşündüyündən fərqli olaraq, əslində daha çox tətbiq olunur: körpülərin, binaların, yolların qurulması, kompas istiqamətləri, hündürlük və məsafələrin ölçülməsi, hətta kompüter qrafikasında istifadə olunur.
Triqonometriyanın tarixi inkişafı və əsas anlayışları
Triqonometriyanın ilk addımları eramızdan əvvəl III minillikdə Babil və Misir riyaziyyatında öz əksini tapıb. Lakin onun müstəqil elm sahəsi kimi formalaşması eramızdan əvvəl II əsrdə yunan riyaziyyatçısı Hipparxın adı ilə bağlıdır. Hipparx ilk dəfə triqonometriya cədvəllərini tərtib etmiş, sferik triqonometriyanın bünövrəsini qoymuşdur. Daha sonra Hindistan və Ərəb riyaziyyatçılarının töhfələri ilə triqonometriya nəzəri cəhətdən zənginləşmiş, sin, kosin, tangent, kotangent anlayışları meydana çıxmışdır.
Triqonometriyanın əsas anlayışları bucaqlar, üçbucaqlar və onların tərəfləri arasında qurulan riyazi münasibətlərə əsaslanır. Əsas triqonometrik funksiyalar – sinus (sin), kosinus (cos), tangent (tan), kotangent (cot), sekant (sec), kosekant (cosec) – hər biri müstəvi və sferik üçbucaqlarda bucaqlar və tərəflər arasında asan hesablamalar aparmaq üçün yaradılıb. Sinus və kosinus anlayışı əslində bir çevrənin radiusu üzərində yerləşən nöqtənin koordinatlarına istinad edir. Bu funksiyalar vasitəsilə hər hansı bir bucağın qarşısındakı tərəfin uzunluğunu, bucağın ölçüsünü və ya üçbucağın sahəsini hesablamaq mümkündür.
Triqonometriyanın əsas tənlikləri və identikləri
Triqonometriyanın əsasını təşkil edən tənlik və identiklər bucaqların və onların funksiyalarının qarşılıqlı əlaqələrini təsvir edir. Ən məşhur triqonometrik identikliklər aşağıdakılardır:
- Sinus Teoremi:
Üçbucağın hər hansı tərəfi, onun qarşısındakı bucağın sinusuna nisbəti bütün üçbucaqlar üçün eynidir.
a/sinA = b/sinB = c/sinC - Kosinüs Teoremi:
Hər hansı bir tərəfin kvadratı, digər iki tərəfin kvadratları cəminin və onların arasındakı bucağın kosinusunun ikiqat hasili ilə fərqinə bərabərdir.
c² = a² + b² – 2ab·cosC - Birinci əsas identiklik:
sin²x + cos²x = 1 - İkinci əsas identiklik:
1 + tan²x = sec²x - Üçüncü əsas identiklik:
1 + cot²x = csc²x
Bu əsas identikliklər triqonometriyanın bütün hesablama və isbatlarının əsasını təşkil edir.
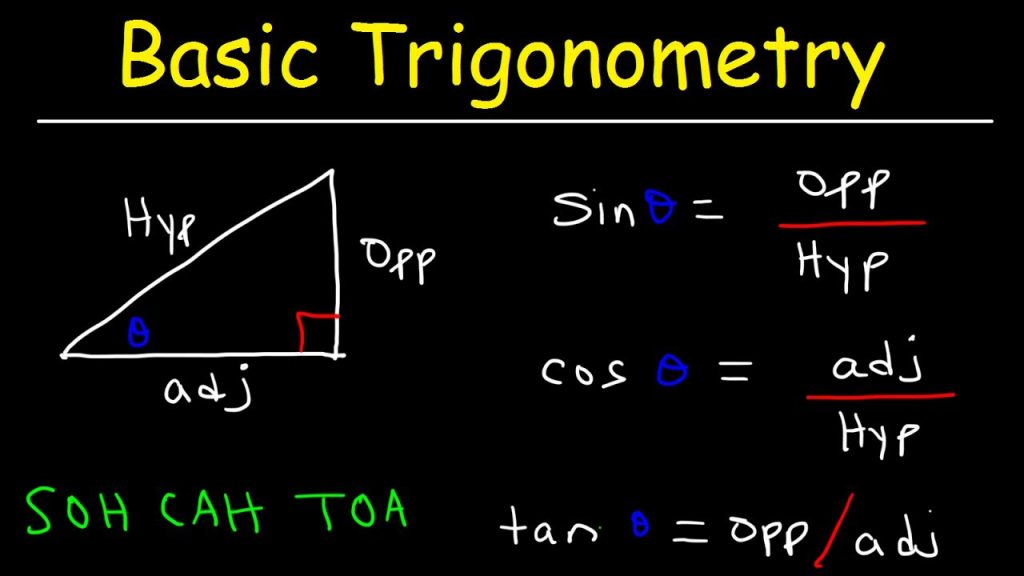
Triqonometriyanın üçbucaqların həllində rolu
Triqonometriyanın ən mühüm praktiki tətbiqlərindən biri müxtəlif tipli üçbucaqların həllində – yəni onların bilinməyən tərəf və bucaqlarının tapılmasında istifadə olunmasıdır. Əgər bir üçbucağın iki tərəfi və aralarındakı bucaq məlumdursa, kosinüs teoremi ilə üçüncü tərəf hesablana bilər. Əgər iki bucaq və bir tərəf məlumdursa, sinus teoremi tətbiq olunur. Hər hansı real həyatda, məsələn, torpaq ölçmə işlərində, topoqrafiyada, mühəndislik layihələrində, hətta göy cisimlərinin məsafəsinin təyinində bu metodlar geniş tətbiq olunur. Triqonometriya astronomiyada, gəmiçilikdə və aviasiyada da bucaqların ölçülməsi və məsafələrin hesablanmasında həlledici əhəmiyyət kəsb edir.
Triqonometriyanın funksiyaları və qrafikləri
Triqonometriyada əsas funksiyaların qrafikləri müəyyən dövri və simmetrik xassələrə malikdir. Sinus və kosinus funksiyaları 0-dan 2π-yə qədər dövrdə özlərini təkrarlayır, yəni dövri funksiyalardır. Tangent və kotangent isə hər π intervalında dövriliyə malikdir. Bu xüsusiyyətlər onların riyazi modelləşdirmədə, harmonik dalğaların təsvirində, periodik hadisələrin analizində əvəzsiz vasitə olmasını təmin edir. Məsələn, sinusoidal dalğalar fizika və mühəndislikdə səs, işıq və elektromaqnit dalğalarının modelləşdirilməsində geniş tətbiq olunur.
Sinus, kosinus və tangent funksiyalarının qrafikləri həmçinin simmetriya, maksimal və minimal nöqtələr, sıfırdan keçmələr və asimptotlarla xarakterizə olunur. Bu xüsusiyyətlər riyaziyyatın digər sahələri, xüsusən də diferensial və inteqral hesabda funksiyaların tədqiqində istifadə olunur.
Triqonometriyanın elmdə və texnikada tətbiq sahələri
Triqonometriya, klassik riyaziyyat sahələrindən fərqli olaraq, birbaşa real dünyada tətbiq oluna bilən elmi aparatdır. Memarlıqda və inşaat mühəndisliyində bucaqların və məsafələrin hesablanması, dəqiq ölçmələr aparmaq üçün istifadə olunur. Fizikada dalğaların yayılması, akustika, optika və elektromaqnit sahələrinin tədqiqində triqonometrik funksiyalardan istifadə edilir. Coğrafiyada koordinatların, hündürlüyün, məsafənin təyini üçün triangulyasiya üsulu tətbiq olunur. Astronomiyada günəş, ay və ulduzların mövqelərinin hesablanması üçün əsas alətdir.
Müasir dövrdə triqonometriya kompüter qrafikasında, süni intellekt alqoritmlərində, peyk və GPS texnologiyalarında, pilotsuz uçuş aparatlarının idarə olunmasında və bir çox digər innovativ sahələrdə istifadə edilir. Hər hansı animasiya, vizual effekt və ya virtual reallıq tətbiqi hazırlananda triqonometrik tənlik və qrafiklər əsas baza rolunu oynayır.
Triqonometriyanın tədrisi və Azərbaycanda riyaziyyat təhsilində yeri
Azərbaycanda triqonometriya həm orta məktəbdə, həm də ali təhsil müəssisələrində riyaziyyatın mühüm bölməsi kimi tədris olunur. Orta məktəblərdə triqonometriya, əsasən, IX-XI siniflərdə xüsusi kurs şəklində keçirilir, ali məktəblərdə isə tətbiqi riyaziyyat, mühəndislik, fizika və digər ixtisaslarda ayrıca modul şəklində öyrədilir. Müəllimlər və tələbələr üçün bir çox dərslik, iş dəftəri, elektron resurs və proqram təminatı hazırlanıb.
Triqonometriyanın tədrisi şagirdlərə məntiqi düşüncə, analiz və problemlərin həllinə yaradıcı yanaşma bacarığı qazandırır. Eyni zamanda, gələcəkdə mühəndis, proqramçı, memar, coğrafiyaçı və ya iqtisadçı kimi peşə seçimi üçün möhkəm baza formalaşdırır. Azərbaycanda riyaziyyat olimpiadalarında, fənn müsabiqələrində, giriş imtahanlarında triqonometrik məsələlər həmişə xüsusi yer tutur.
Triqonometriyanın elmi və fəlsəfi əhəmiyyəti
Triqonometriya yalnız riyaziyyatın tətbiqi sahəsi kimi yox, eyni zamanda insanın təfəkkürünün və təbiəti anlamaq bacarığının bariz nümunəsidir. Üçbucaqlar, bucaqlar və onların harmoniyası kainatın strukturunda, təbiət hadisələrinin qanunauyğunluğunda, bədii və memarlıq əsərlərində, hətta musiqidə öz əksini tapır. Triqonometrik funksiyaların riyazi harmoniyası insanı kainatdakı nizama, simmetriyaya və gözəlliyə valeh edir. Ən mürəkkəb riyazi modellər, nəzəri fizikada simmetriya qanunları və hətta kvant mexanikası triqonometriyanın əsaslarına söykənir.
Triqonometriya bəşər sivilizasiyasının ən böyük elmi nailiyyətlərindən biridir. Onun kökləri qədim sivilizasiyalara, inkişafı isə müasir elm və texnologiyalara bağlıdır. Triqonometriya vasitəsilə insan təbiətin sirlərini açır, kainatın strukturu və harmoniyasını riyazi dillə ifadə edir. Onun prinsipləri əsasında yaradılan elmi və texniki nailiyyətlər insan həyatının bütün sahələrində inkişaf və tərəqqinin əsasını qoyur. Triqonometriya tədrisi yeni nəsil üçün intellektual inkişaf, elmi dünyagörüş, yaradıcı düşüncə və peşəkar bacarıqların formalaşmasında həlledici rol oynayır. Bu sahədə əldə olunan nailiyyətlər Azərbaycanın elm və təhsil ənənələrində də öz əksini tapır.
Ən Çox Verilən Suallar
-
Triqonometriya nədir və hansı anlayışları əhatə edir?
Triqonometriya bucaqlar, üçbucaqlar və onların tərəfləri arasındakı riyazi əlaqələri öyrənən riyaziyyat bölməsidir. Əsas anlayışlara sinus, kosinus, tangent, kotangent və bucaqlar daxildir. -
Triqonometrik funksiyalar hansılardır və necə istifadə olunur?
Əsas funksiyalar – sin, cos, tan, cot, sec, csc – üçbucaqlarda tərəf və bucaqların hesablanması, dalğaların təhlili, periodik proseslərin modelləşdirilməsi üçün istifadə olunur. -
Triqonometriya real həyatda hansı sahələrdə tətbiq olunur?
Memarlıq, inşaat, astronomiya, fizika, mühəndislik, naviqasiya, kompüter qrafikası, coğrafiya və GPS texnologiyalarında geniş tətbiq olunur. -
Triqonometriyanın əsas tənlikləri hansılardır?
Sinus teoremi, kosinüs teoremi, əsas triqonometrik identikliklər – sin²x+cos²x=1, 1+tan²x=sec²x, 1+cot²x=csc²x. -
Triqonometrik qrafiklər hansı xassələrə malikdir?
Sinus və kosinus dövri, tangent və kotangent isə hər π intervalında dövriliyə malikdir. Qrafiklər simmetriya, maksimal və minimal nöqtələrlə xarakterizə olunur. -
Triqonometriya necə və nə üçün tədris olunur?
Azərbaycanda orta və ali məktəblərdə tədris olunur, məqsəd şagirdlərdə məntiqi və yaradıcı düşüncə, riyazi bilik və praktiki bacarıq formalaşdırmaqdır. -
Triqonometriyanın tarixi inkişafı nədən ibarətdir?
Kökləri qədim Babil, Misir, Yunan, Hindistan və Ərəb riyaziyyatına gedib çıxır. Elm sahəsi kimi Yunan riyaziyyatçısı Hipparx tərəfindən formalaşdırılıb. -
Triqonometriya olimpiada və imtahanlarda necə tətbiq olunur?
Çoxsaylı məsələ və problemlərin həllində, üçbucaqların, bucaqların, qrafiklərin, identikliklərin öyrənilməsində istifadə olunur. -
Triqonometrik funksiyalar arasında necə keçid aparılır?
Əsas identiklik və tənliklər vasitəsilə bir funksiyadan digərinə asanlıqla keçid mümkündür. -
Triqonometriya müasir texnologiyalarda necə istifadə olunur?
Peyk və GPS sistemlərində, kompüter animasiyası və qrafikasında, robot texnikasında, elmi simulyasiyalarda əsas rol oynayır.