Üçbucaqlar: Tərifi, Təsnifatı, Elementləri

Üçbucaq insanın təbiəti anlamağa başladığı ilk dövrlərdən bəri həndəsənin mərkəzində duran və formaca sadə görünsə də, mahiyyət etibarilə çox qatlı riyazi və fiziki əlaqələri özündə cəmləyən bir fiqurdur. O, üç nöqtə və bu nöqtələri birləşdirən üç düz xəttin əmələ gətirdiyi ən əsas çoxbucaqlı formadır. Təbiətdə, texnologiyada, arxitekturada, elmdə və gündəlik həyatda rast gəlinən bu fiqur, həm struktur baxımından sabitliyi, həm də məntiqi baxımdan hesablama qabiliyyətini simvolizə edir.

Riyaziyyatda üçbucaq anlayışı yalnız elementar məktəb mövzusu kimi deyil, eyni zamanda ali səviyyəli hesablamaların və nəzəriyyələrin də əsasını təşkil edir. Bu fiqur vasitəsilə məsafələr ölçülür, açılar tapılır, kosmik peyklərin mövqeyi hesablanır, mühəndislik qurğuları sabitləşdirilir. Onun üzərində qurulan qanunlar, xüsusilə Pifaqor teoremi, trigonometriya və sahə düsturları, riyazi düşüncənin ən fundamental dayaqları hesab olunur.

Üçbucağın Tərifi və Əsas Xüsusiyyətləri

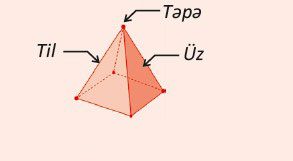
Üçbucaq, düz müstəvidə yerləşən və üç nöqtə ilə müəyyən olunan ən sadə çoxbucaq formasıdır. Onun üç tərəfi və üç daxili bucağı olur. Üçbucaqlar həm təbiətdə, həm də memarlıq, mühəndislik və riyaziyyat sahələrində geniş istifadə olunur. Riyaziyyatda bu fiqur əsas element hesab edilir və digər mürəkkəb fiqurların öyrənilməsi üçün baza təşkil edir. Üçbucağın sadə quruluşuna baxmayaraq, onun əhatə etdiyi riyazi anlayışlar olduqca dərin və çoxşaxəlidir.

Üçbucaqların əlamətləri bunlardır: üç tərəf, üç bucaq, üç təpə nöqtəsi və bucaqların cəminin 180° olması. Bu qanun istənilən üçbucağa aiddir və onun əsas təməl prinsipidir.

Üçbucaqların Təsnifatı

Üçbucaqlar müxtəlif əlamətlərə görə təsnif edilə bilər. İki əsas meyara əsasən təsnifat aparılır: tərəflərinə görə və bucaqlarına görə.

Tərəflərinə görə:

1. Bərabəryanlı üçbucaq – İki tərəfi və iki bucağı bərabər olur.
2. Bərabərtərəfli üçbucaq – Bütün tərəfləri və bucaqları bərabərdir. Hər bucağı 60°-dir.
3. Müxtəlifyanlı üçbucaq – Tərəfləri və bucaqları bir-birindən fərqlidir.

Bucaqlarına görə:

1. Kəskinbucaqlı üçbucaq – Bütün bucaqları 90°-dən kiçikdir.
2. Düzbucaqlı üçbucaq – Bir bucağı dəqiq 90°-dir. Bu cür üçbucaqlarda Pifaqor teoremi tətbiq olunur.
3. Korbuçaqlı üçbucaq – Bir bucağı 90°-dən böyükdür.

Bu təsnifatlar yalnız nəzəri deyil, həm də praktik tətbiq baxımından vacib əhəmiyyət daşıyır. Mühəndislik layihələrində və memarlıq konstruksiyalarında bu ayrım ciddi şəkildə nəzərə alınır.

Üçbucağın Elementləri və Simmetriyası

Üçbucağın əsas elementlərinə tərəflər, bucaqlar, medianalar, hündürlüklər, bucaqortalar və orta xətlər daxildir. Hər bir elementin özünəməxsus funksiyası və rolu vardır. Məsələn, medianalar – üçbucağın təpə nöqtəsini qarşı tərəfin orta nöqtəsi ilə birləşdirir. Bütün medianalar bir nöqtədə (mərkəz) kəsişir. Bu nöqtəyə ağırlıq mərkəzi deyilir.

Hündürlük – təpə nöqtədən qarşı tərəfə perpendikulyar endirilmiş düz xəttdir. Düzbucaqlı üçbucaqda hündürlük hipotenüz üzərində yerləşir.
Bucaqların ortası – bucağı iki bərabər hissəyə bölən şüadır.
Orta xətlər – bir tərəfin iki ucu ilə digər tərəfdəki orta nöqtəni birləşdirən xətdir.

Bərabərtərəfli və bərabəryanlı üçbucaqlarda simmetriya mərkəzi və oxları mövcuddur ki, bu da onları daha stabil və estetik cəhətdən cəlbedici edir.

Pifaqor Teoremi və Üçbucaqlarda Tətbiqi

Düzbucaqlı üçbucaqlarda ən məşhur teorem Pifaqor teoremidir. Bu teoremə əsasən, hipotenüzün kvadratı digər iki katetin kvadratlarının cəminə bərabərdir. Riyazi ifadə ilə:

c² = a² + b²

Bu düstur, yalnız düzbucaqlı üçbucaqlara aiddir və geometriyada çox geniş tətbiq sahəsinə malikdir. Məsafənin ölçülməsi, qısa yolun tapılması, memarlıq quruluşları və riyazi sübutlar bu düsturla əsaslandırılır.

Üçbucağın Sahəsi və Perimetri

Üçbucağın sahəsi və perimetri onun əsas ölçülərindən biridir. Sahəni hesablamaq üçün bir neçə üsul mövcuddur:

1. Ən sadə düstur:
   S = (a × h) / 2
   Burada a – əsas tərəf, h – hündürlükdür.
2. Heron düsturu:
   S = √[p(p−a)(p−b)(p−c)]Burada p – yarımperimetr, a, b, c – tərəflərdir.

Perimetrin hesablanması üçün sadəcə bütün tərəflər toplanır:
P = a + b + c

Bu düsturlar yalnız nəzəriyyə üçün deyil, praktiki məsələlərdə, torpaq ölçmələrində, memarlıq layihələrində də geniş istifadə olunur.

Üçbucaqlarda Daxilə və Xaricə Çəkilmiş Dairələr

Üçbucağın daxilinə və xaricinə çəkilən dairələr onun geometriyasının xüsusi elementləridir.

• Daxilə çəkilmiş dairə – üçbucağın bütün tərəflərinə toxunan və içərisində yerləşən yeganə dairədir. Onun mərkəzi bucaqortaların kəsişmə nöqtəsində yerləşir.
• Xaricə çəkilmiş dairə – üç təpə nöqtəsindən keçən yeganə dairədir. Onun mərkəzi isə orta perpendikulyarların kəsişmə nöqtəsidir.

Bu dairələr müstəvi və dairəvi simmetriyanın riyazi izahında mühüm yer tutur. Xüsusilə, trigonometriyada bu dairələrin radiusları vasitəsilə bucaqların sinus, kosinus, tangens dəyərləri hesablanır.

Trigonometriya və Üçbucaqlar

Üçbucaqlar trigonometrik funksiyaların əsasını təşkil edir. Sinus, kosinus, tangens və kotangens kimi anlayışlar, əsasən üçbucaqların bucaqları və tərəfləri arasında olan əlaqələri göstərir.

Sinus teoremi:
a / sin A = b / sin B = c / sin C

Kosinus teoremi:
c² = a² + b² – 2ab·cos C

Bu teoremlər qeyri-düzbucaqlı üçbucaqlarda tərəflərin və bucaqların hesablanmasında istifadə olunur. Həmçinin GPS texnologiyasında, peyk ölçmələrində, riyazi modellərdə bu funksiyalar geniş yer tutur.

Üçbucaqların Həyatda və Tətbiqatda Yeri

Üçbucaq təkcə riyaziyyatda deyil, gündəlik həyatın müxtəlif sahələrində də qarşımıza çıxır. Mühəndislikdə üçbucaqlar konstruksiya sabitliyi üçün ideal formadır. Körpülərin dayaqları, polad konstruksiyalar, dam örtükləri və aerodinamik konstruksiyalar bu formaya əsaslanır.

İncəsənətdə, xüsusilə islam memarlığında və miniatürlərdə üçbucağın mütənasib və estetik quruluşu istifadə olunur. Eyni zamanda üçbucaq forması rəmz olaraq çoxlu mənaları ifadə edir: tarazlıq, harmoniya və sabitlik.

Üçbucağın mexaniki baxımdan dayanıqlı olması onu tikinti və texnologiya sahəsində ideal modelə çevirir. Bu səbəbdən üçbucaqlar həm simvolik, həm də funksional baxımdan xüsusi mövqeyə malikdir.

Üçbucaqların Riyazi Əhəmiyyəti və Təhsil Sistemində Rolu

Üçbucaqlar məktəb riyaziyyatının ən mühüm bölmələrindən biridir. Onlar vasitəsilə şagirdlər həm həndəsəni, həm də alqoritmik düşünmə qabiliyyətini inkişaf etdirirlər. Hər riyaziyyat dərsliyində üçbucaqlara aid bölmə xüsusi yer tutur. Onların öyrənilməsi şagirdlərə məkan, ölçü və istiqamət anlayışlarını mənimsəməyə kömək edir.

Təhsil sahəsində üçbucaqlar riyazi məntiqin formalaşdırılmasında əsas mərhələdir. Sadəliklə yanaşı, mürəkkəbliyi əhatə edən bu fiqur tələbələrə həm bazanı, həm də üst səviyyə anlayışları qavramağa imkan yaradır.

Üçbucaq həm ən sadə, həm də ən dərin mənalı riyazi fiqurlardan biridir. Onun forması sadə görünsə də, içərisindəki riyazi və məntiqi əlaqələr son dərəcə mürəkkəb və maraqlıdır. Bu fiqur riyaziyyatın özəyidir və digər bütün həndəsi anlayışların qurulmasında başlanğıc nöqtə rolunu oynayır. Həm nəzəri, həm tətbiqi sahələrdə mühüm yer tutan üçbucaqlar həyatımızın hər sahəsində özünə yer tapır. Bu fiqurun təhlili yalnız riyazi deyil, həm də texnoloji, mühəndislik və mədəni baxımdan dəyərləndirilməlidir. Üçbucaqların öyrənilməsi həm bilik, həm də təfəkkür inkişafı üçün zəruri elementdir.

Ən Çox Verilən Suallar