Geometriyada uyğun tərəfləri paralel olan bucaqlar çox qədim dövrlərdən bəri öyrənilən və fundamental məfhumlar sırasında yer alır. Bu mövzuya toxunmadan əvvəl ümumiyyətlə paralellik və bucaq kimi riyazi anlayışların necə formalaşdığına nəzər salmaq vacibdir. Antik dövr riyaziyyatçıları, xüsusilə qədim yunanlar paralel xətlərin xüsusiyyətlərini və bu xətlərin kəsişməsindən yaranan bucaqların müxtəlif növlərini araşdırmışlar. Öklid “Elementlər” əsərində paralel xətlərin bir-biri ilə əlaqəsini və bu kontekstdə yaranan bucaqların müxtəlif kateqoriyalarını ayrıca qeyd edir. Uyğun tərəfləri paralel olan bucaqlar isə məhz bu araşdırmaların təməlində dayanır və klassik həndəsədə, həmçinin müasir riyaziyyatın müxtəlif istiqamətlərində aktual olaraq istifadə edilir.
Bir çox həndəsi fiqurda, xüsusilə paralel tərəfli çoxbucaqlılarda (kvadrat, düzbucaqlı, parallelogram və s.) uyğun tərəflər arasında yaranan bucaqların xüsusiyyətləri müxtəlif riyazi məsələlərin həllində vacib rol oynayır. Bu konsepsiya yalnız düz bucaqlı fiqurlarda deyil, mürəkkəb çoxbucaqlılarda, poliqonlarda və hətta bəzən çoxölçülü həndəsə modellərində də tətbiq olunur.
Uyğun tərəflərin paralelliyinin formalaşma qaydaları və riyazi əsaslandırılması
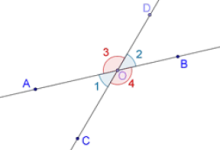
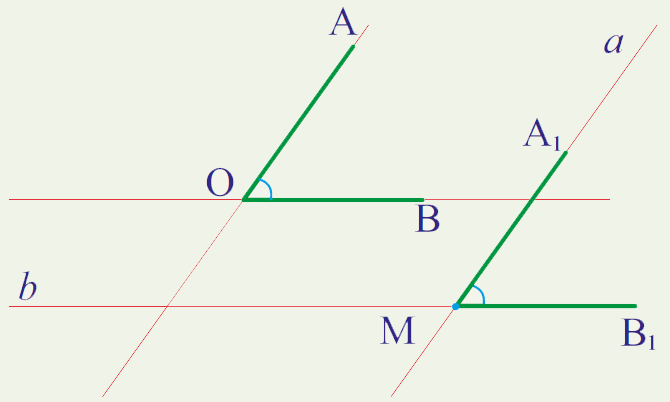
Uyğun tərəfləri paralel olan bucaqlar dedikdə, iki müxtəlif bucağın hər birinin uyğun tərəflərinin bir-birinə paralel olması nəzərdə tutulur. Riyaziyyatda bu məfhum əsasən oxşar fiqurlar arasında və ya müəyyən növ çoxbucaqlıların tədqiqində qarşımıza çıxır. Əgər iki bucaq götürülürsə və onların birinci və ikinci şüaları bir-biri ilə uyğun ardıcıllıqla paraleldirsə, bu bucaqlar uyğun tərəfləri paralel olan bucaqlar adlanır. Misal üçün, AOB və COD bucaqları üçün AO || CO, OB || OD olarsa, bu iki bucaq uyğun tərəfləri paralel olan bucaqlardır.
Bu riyazi yanaşmanın əsas məqsədi bucaqların ölçülərinin bərabərliyini, onların yerləşməsindəki simmetriyanı və həndəsi fiqurun digər elementləri ilə olan əlaqəsini dəqiq şəkildə müəyyənləşdirməkdir. Belə bucaqların əsas xüsusiyyətlərindən biri də onların ölçülərinin mütləq bərabər olmasıdır. Yəni uyğun tərəfləri paralel olan iki bucaq, hər zaman bir-birinə bərabər olur. Bu nəticə paralel xətlərin və şüaların riyazi tərifinə və bucaqların təyin olunması prinsiplərinə əsaslanır.
Uyğun tərəfləri paralel olan bucaqların sinifləndirilməsi və əsas növləri
Uyğun tərəfləri paralel olan bucaqlar müxtəlif konfiqurasiyalarda meydana çıxa bilər. Ən geniş yayılmış forması iki düz xəttin üçüncü bir xətt tərəfindən kəsişməsi zamanı yaranan bucaqlardır. Bu hal xüsusilə paralel xətlərin kəsişmə nöqtələrində və ya transversalla bağlı məsələlərdə tez-tez müşahidə olunur. Belə məsələlərdə alınan bucaqlara alternativ daxili, xarici və uyğun bucaqlar deyilir. Alternativ daxili bucaqlar bir-birinə qarşı tərəflərdə yerləşir, lakin uyğun tərəfləri paralel olan bucaqlar üçün əsas meyar hər iki bucağın tərəflərinin ardıcıl şəkildə bir-biri ilə paralel olmasıdır.
Digər bir nümunə paralel tərəfli çoxbucaqlılarda rast gəlinir. Burada hər bir cüt paralel tərəf üzərində qurulan bucaqlar istər çoxbucaqlının daxili bucaqları, istərsə də xarici bucaqlar şəklində özünü göstərir. Bu fiqurlarda, adətən, bucaqların ölçüləri bir-birinə bərabər olur və uyğun tərəflərin paralelliyi sayəsində bu bərabərlik qorunur. Xüsusilə paralel tərəfli trapeziyada uyğun bucaqların öyrənilməsi vacib yer tutur.
Aşağıdakı cədvəldə ən çox rast gəlinən uyğun tərəfləri paralel olan bucaqlar və onların əsas xüsusiyyətləri təqdim olunur:
| Bucaqların növü | Fiqurun tipi | Paralel tərəflər | Bucaqların bərabərliyi | Xüsusi hallar |
|---|---|---|---|---|
| Daxili uyğun bucaqlar | Paralel xətlər + transversa | a | b, c transversa | |
| Xarici uyğun bucaqlar | Paralel xətlər + transversa | a | b, c transversa | |
| Paralel tərəfli çoxbucaqlının bucaqları | Düzbucaqlı, parallelogram | Qarşı tərəflər | Hər iki cüt bucaq bərabərdir | Simmetriya vardır |
| Trapeziyada baza bucaqları | Trapeziya | Baza tərəflər | Hər bir baza bucaqları bərabərdir | Yalnız bərabəryanlı trapeziyada |
Bu cədvəl riyazi kontekstdə müxtəlif fiqurlarda paralel tərəflərin yaratdığı uyğun bucaqların ümumi xülasəsini verir və tətbiq sahələrinin konturlarını daha aydın göstərir.
Uyğun tərəfləri paralel olan bucaqların əsas xüsusiyyətləri
Bu tip bucaqların ən əsas və dəyişməz xüsusiyyəti onların ölçülərinin həmişə bərabər olmasıdır. Belə ki, əgər iki bucağın uyğun tərəfləri bir-birinə paraleldirsə, həmin bucaqların dərəcə ölçüləri də mütləq bərabər olacaq. Riyazi sübut üçün aşağıdakıları əsas götürmək olar:
- Paralel xətlərin eyni istiqamətdə olması onların arasındakı məsafənin sabit qalmasını təmin edir. Bu da həmin xətlər üzərində qurulmuş bucaqların eyni dərəcə ilə ölçülməsinə gətirib çıxarır.
- Uyğun tərəfləri paralel olan bucaqlarda, əgər bir bucağın hər bir şüası digər bucağın uyğun şüası ilə paraleldirsə, burada yaranan həndəsi simmetriya bucaqların üst-üstə düşməsini təmin edir.
- Müxtəlif həndəsi transformasiyalar — fırlanma, paralel köçürmə və digər çevirmələr — zamanı uyğun tərəfləri paralel olan bucaqlar öz ölçülərini itirmir və bərabər qalır.
Əlavə olaraq qeyd etmək lazımdır ki, bu prinsip yalnız klassik Evklid həndəsəsində deyil, həm də analitik həndəsə və hətta çoxölçülü riyazi modellərdə də öz əksini tapır.
Praktiki tətbiqlər və gündəlik həyatda uyğun tərəfləri paralel olan bucaqlar
Riyazi nəzəriyyələr çox vaxt gündəlik həyatda, texnikada, memarlıqda, mühəndislikdə və bir çox digər sahələrdə real tətbiqlər tapır. Uyğun tərəfləri paralel olan bucaqlar da bu baxımdan istisna deyil.
Memarlıqda binaların düzgün bucaq altında yerləşdirilməsi, paralel elementlərin simmetriyası və estetikasının qorunması üçün bu konsepsiya olduqca vacibdir. Məsələn, körpülərin dayaqlarının paralel şəkildə qurulması, binaların fasadında simmetrik pəncərə və qapıların yerləşdirilməsi məhz bu prinsiplərə əsaslanır. Eyni zamanda, yol çəkilişində, avtomobil yollarının bir-birinə paralel və bucaqlı şəkildə salınmasında bu riyazi yanaşmadan istifadə olunur.
Texniki sahələrdə, xüsusilə mexanika və robot texnikasında, paralel və bucaq əlaqələrinə əsaslanan konstruksiyalarda mühəndislər uyğun tərəfləri paralel olan bucaqların hesablamalarına tez-tez müraciət edirlər. Elektronika sxemlərində və həndəsi ölçülərdə də eyni yanaşmanın tətbiqinə rast gəlinir. Həmçinin, bu cür riyazi biliklər dizayn və incəsənətdə simmetriya yaratmaq üçün də vacibdir.
Uyğun tərəfləri paralel olan bucaqların təhlilinin vacibliyi və riyazi əhəmiyyəti
Geometriyada bəzən birmənalı olmayan və ya təhrif olunmuş təsəvvürlərin qarşısını almaq üçün dəqiq terminologiya və riyazi yanaşmalar zəruridir. Uyğun tərəfləri paralel olan bucaqlar məsələsi də bu baxımdan vacibdir, çünki bir çox məsələ və tapşırığın dəqiq və tez həlli üçün bu biliklərin düzgün tətbiqi mühüm rol oynayır. Riyazi olçü alətlərindən və proqram təminatından istifadə edərkən, bu tip bucaqların dəqiq təyin olunması və analizi nəticənin düzgünlüyünü təmin edir.
Bir çox məktəb dərsliklərində bu mövzu səthi şəkildə izah edilsə də, əslində dərin həndəsi bilik və analitik təhlil tələb edir. Hər bir paralel xətlər sistemi, uyğun bucaqlar və onların analizi istənilən mürəkkəb fiqurun riyazi modelinin qurulmasında, sahələrin hesablanmasında, simmetrik strukturların yaradılmasında və digər sahələrdə vacib rol oynayır.
Paralel xətlərin kəsişməsində yaranan uyğun bucaqlar və riyazi sübutlar
İki paralel xətt bir transversalla kəsişdikdə dörd növ bucaq yaranır: daxili, xarici, uyğun və alternativ bucaqlar. Uyğun bucaqlar həmin xətlərin bir tərəfində yerləşir və tərəfləri uyğun şəkildə paraleldir. Riyaziyyatda bucaqların bərabərliyinin sübutu üçün əsas vasitə bu paralellikdən istifadədir.
Sübut üçün aşağıdakı ardıcıllıqdan istifadə edilir:
- İki paralel xətt a və b, onları kəsən transversa c xətti olsun.
- Xəttlərin kəsişmə nöqtələrində yaranan uyğun bucaqların biri α, digəri isə β ilə işarə olunsun.
- Paralellik prinsipinə əsasən, α və β həmişə bir-birinə bərabər olur.
Bu sübut riyazi məntiqin və həndəsi konsepsiyaların praktiki tətbiqi baxımından olduqca sadə, eyni zamanda fundamental əhəmiyyət daşıyır.
Uyğun tərəfləri paralel olan bucaqların gündəlik riyaziyyat və təhsil prosesində yeri
Məktəb riyaziyyatında uyğun tərəfləri paralel olan bucaqlar mövzusu, şagirdlərin məntiqi düşüncə və həndəsi təsəvvürlərinin formalaşmasında əsas rol oynayır. Bu biliklər riyaziyyat fənninin təməl hissələrindən biridir və təkcə orta məktəb səviyyəsində deyil, ali təhsil pilləsində də davamlı olaraq öyrədilir. Bundan əlavə, riyazi olçü və analiz proqramlarında, eləcə də, texnoloji və proqramlaşdırma alqoritmlərində də bu biliklərə ehtiyac yaranır. Müasir proqramlaşdırma dillərində, 3D modelləşdirmə proqramlarında uyğun tərəfləri paralel olan bucaqların hesablanması üçün ayrıca modullar hazırlanır. Bu da onların riyazi təhsildə, texnologiyada və müxtəlif peşə sahələrində əhəmiyyətini artırır.
Uyğun tərəfləri paralel olan bucaqlar həndəsənin əsas anlayışlarından biridir və riyaziyyatın bir çox bölmələrində aparıcı rol oynayır. Onların nəzəri əsasları, riyazi sübutları və praktiki tətbiqləri müxtəlif sahələrdə — memarlıqdan mühəndisliyə, təhsildən texnologiyaya qədər geniş şəkildə istifadə olunur. Bu tip bucaqların analizi və təhlili həndəsi biliklərin dərinləşdirilməsi, dəqiq riyazi düşüncənin inkişafı və məntiqi mühakimə bacarıqlarının formalaşdırılması baxımından böyük əhəmiyyət daşıyır. Uyğun tərəfləri paralel olan bucaqların riyazi və tətbiqi əhəmiyyəti onların tədris prosesində, eləcə də gündəlik həyatda daim aktual qalmasını təmin edir. Bu biliklər həm nəzəri, həm də praktiki səviyyədə istifadəçi üçün geniş imkanlar açır və riyazi düşüncənin inkişafında vacib yer tutur.
Ən Çox Verilən Suallar
Uyğun tərəfləri paralel olan bucaqlar dedikdə, iki bucağın hər bir tərəfinin digər bucağın uyğun tərəfi ilə paralel olması başa düşülür. Bu halda, bucaqlardan birinin ilk tərəfi digərinin ilk tərəfinə, ikinci tərəfi isə digərinin ikinci tərəfinə paralel olur. Belə bucaqların ən əsas xüsusiyyəti onların həmişə ölçücə bərabər olmasıdır. Bu məfhum riyaziyyatda, xüsusilə həndəsədə oxşar fiqurların və paralel xətlərin öyrənilməsində mühüm rol oynayır.
İki bucağın uyğun tərəfləri bir-birinə ardıcıllıqla paralel olduqda həmin bucaqlar uyğun tərəfləri paralel olan bucaqlar hesab olunur. Riyazi olaraq, bu vəziyyətdə hər bir tərəfin istiqaməti və yerləşməsi digər bucaqdakı uyğun tərəfin istiqaməti ilə tam üst-üstə düşür. Bu, həndəsədə tez-tez paralel xətlərin transversalla kəsişməsi zamanı meydana çıxır.
Bu cür bucaqların ən mühüm xüsusiyyəti onların həmişə bərabər olmasıdır. Başqa sözlə, əgər iki bucağın uyğun tərəfləri paraleldirsə, bu bucaqların ölçüləri də eyni olur. Bu xüsusiyyət paralel xətlərin quruluşundan və həndəsi simmetriya prinsiplərindən irəli gəlir. Eyni zamanda, uyğun tərəfləri paralel olan bucaqlar istənilən çevirmə və fırlanma zamanı öz ölçüsünü itirmir.
Bu tip bucaqlar gündəlik həyatda memarlıqda, inşaatda, texnikada, yol çəkilişində və dizaynda simmetriyanı və düzgün bucaqlılığı təmin etmək üçün istifadə edilir. Məsələn, binaların düzgün bucaqda tikilməsi, körpülərin dayaqlarının paralel yerləşdirilməsi, eləcə də, avtomobil yollarının çəkilişində uyğun tərəfləri paralel olan bucaqların hesablanmasına ehtiyac yaranır.
Məktəb riyaziyyatında bu mövzu əsasən paralel xətlərin transversalla kəsişməsi kontekstində izah edilir. Şagirdlərə, paralel xətlərin bir-biri ilə necə əlaqəli olduğu, yaranan uyğun, alternativ və daxili bucaqların hansı qaydalara əsaslandığı müxtəlif vizual modellər və məsələlər üzərində öyrədilir. Bu, məntiqi və həndəsi düşüncə bacarığını inkişaf etdirir.
Bu anlayışlar oxşar səslənsə də, fərqli riyazi məfhumlardır. Uyğun bucaqlar dedikdə, paralel xətlərin bir transversalla kəsişməsində eyni mövqedə yerləşən bucaqlar nəzərdə tutulur. Uyğun tərəfləri paralel olan bucaqlar isə, iki müxtəlif bucağın bütün tərəflərinin ardıcıllıqla bir-birinə paralel olması halıdır. Hər uyğun tərəfləri paralel olan bucaq uyğun bucaq ola bilər, lakin əksinə həmişə belə olmur.
Düzbucaqlı, kvadrat və parallelogram kimi fiqurlarda qarşı tərəflər paralel olur və bu tərəflər üzərində qurulan bucaqlar həmişə bərabər olur. Belə hallarda, paralel tərəflərin hər birində yaranan bucaqlar, uyğun tərəfləri paralel olan bucaqlar adlanır və fiqurun bütün simmetrik xüsusiyyətlərini qoruyur. Trapeziyada isə yalnız baza tərəfləri paralel olur və müvafiq baza bucaqları bərabər olur.
Bəli, uyğun tərəfləri paralel olan bucaqların əsas riyazi qanunu onların ölçülərinin tam bərabər olmasıdır. Bu, paralel xətlərin və şüaların fundamental xüsusiyyətlərindən irəli gəlir. Əgər bir bucağın hər iki tərəfi digər bucağın uyğun tərəfi ilə paraleldirsə, həmin bucaqların dərəcə ölçüləri də eyni olacaq.
Praktikada bu tip bucaqların tapılması üçün müxtəlif həndəsi alətlər, proqnozlaşdırma proqramları, CAD proqramları və ölçü cihazlarından istifadə edilir. Vizual modelləşdirmə və analitik hesablama yanaşmaları ilə, istər manual, istərsə də rəqəmsal mühitdə bu bucaqların ölçüləri asanlıqla təyin oluna bilər. Riyazi sübutlar və formulalar bu hesablamanı daha da dəqiqləşdirir.
Bəzən şagirdlər üçün paralel və uyğun anlayışlarını qarışdırmaq, bucaqların yerləşməsini vizual təsəvvür etmək və bucaqların ardıcıllığını düzgün müəyyənləşdirmək çətin ola bilər. Dərslərdə vizual alətlərdən, modellərdən və gündəlik həyatdan nümunələrdən istifadə bu çətinlikləri aradan qaldırmağa kömək edir. Riyazi məntiqin və həndəsi düşüncənin inkişafı bu mövzunun öyrədilməsində əsas məqsəddir.