Riyaziyyat elmində “bucaqlar” və onların qarşılıqlı əlaqələri, xüsusən də perpendikulyar (düz bucaqlı) münasibətləri həm fundamental, həm də tətbiqi baxımdan xüsusi əhəmiyyət daşıyır. Əsrlər boyu müxtəlif mədəniyyətlərdə riyaziyyatçılar bucaq və tərəflərin bir-birinə olan mövqeləri ilə bağlı tədqiqatlar aparıb, bu sahədə yeni anlayışlar formalaşdırıblar. Həyatda bir çox fiziki proseslərin, texnoloji qurğuların və hətta memarlıq əsərlərinin təməlində uyğun tərəfləri perpendikulyar olan bucaqların prinsipial rolu var. Bu konsepsiya yalnız həndəsə və trigonometriyada deyil, həm də mühəndislikdə, fizika və kompüter qrafikasında geniş tətbiq edilir.
Düz bucaq anlayışı, yəni tərəfləri bir-birinə 90 dərəcə təşkil edən bucaqlar, insanın məkan oriyentasiyasının formalaşmasında, alətlərin və cihazların düzgün işləməsində, eləcə də ənənəvi və müasir memarlıqda konstruktiv əsasdır. Müxtəlif obyektlərin və fiqurların perpendikulyar yerləşməsi, onların sabitliyini, dayanıqlığını və funksionallığını təmin edir.
Perpendikulyar olan bucaqların əsas anlayışı
Perpendikulyar bucaqlar, iki tərəfin bir-biri ilə 90 dərəcəlik bucaq altında kəsişməsini ifadə edir. Həndəsə elmində bu münasibət çox mühüm yer tutur. Əgər iki düz xətt və ya kənar, bir nöqtədə elə kəsişirsə ki, aralarındakı bucaq tam olaraq 90° olur, deməli onlar perpendikulyardır. Bu cür münasibət riyaziyyatda yalnız cizgilər arasında deyil, eyni zamanda çoxbucaqlıların, fiqurların və vektorların komponentləri arasında da müşahidə olunur.
Perpendikulyarlıq bir çox həndəsi fiqurun tərifində və əsas xüsusiyyətlərində xüsusi rol oynayır. Məsələn, kvadratın və düzbucaqlının bütün daxili bucaqları 90° olur və bütün tərəfləri bir-birinə perpendikulyardır. Bu münasibət yalnız riyazi təsvir deyil, praktiki olaraq da ölçü və quruluş işlərində sabitlik və düzgünlük deməkdir.
Uyğun tərəf və uyğunluq anlayışının mahiyyəti
Uyğun tərəflər riyaziyyatda, xüsusilə də həndəsə və trigonometriyada müxtəlif fiqurlar arasında müqayisə apararkən istifadə olunan fundamental anlayışdır. İki və ya daha çox fiqur müqayisə edilərkən, onların uyğun tərəfləri dedikdə – uzunluqları və yerləşməsi baxımından bir-birinə bərabər və ya nisbətdə olan tərəflər nəzərdə tutulur.
Məsələn, iki bərabəryanlı üçbucağın uyğun tərəfləri, onların bərabər uzunluqlu kənarlarıdır. Əgər uyğun tərəflər perpendikulyar vəziyyətdədirsə, bu, həmin fiqurlar arasında xüsusi əlaqənin mövcudluğuna işarədir. Uyğunluq yalnız uzunluq və bucaq ölçüləri baxımından deyil, həm də tərəflərin qarşılıqlı yerləşməsi və istiqaməti baxımından öyrənilir.
Uyğun tərəfləri perpendikulyar olan bucaqların riyazi izahı
Riyaziyyatda “uyğun tərəfləri perpendikulyar olan bucaqlar” termini, əsasən iki fiqurun və ya iki müxtəlif obyektin müəyyən uyğun tərəflərinin bir-birinə perpendikulyar olmasını bildirir. Bu hal ən çox eynitərəfli və ya bərabəryanlı üçbucaqlarda, kvadrat və düzbucaqlılarda, eləcə də paralel və perpendikulyar vektorlarda özünü göstərir.
Əgər iki üçbucağın uyğun tərəflərindən biri digərinə perpendikulyar olursa, bu, onların bərabərlik, oxşarlıq və ya digər xüsusi həndəsi əlaqələri barədə dərin təhlil aparmağa imkan verir. Məsələn, A və B üçbucaqlarında AB və DE tərəfləri uyğun tərəflər kimi qəbul edilib, bu tərəflər 90° bucaq altında yerləşirsə, bu, fiqurlar arasında mühüm riyazi münasibətin formalaşdığını göstərir. Perpendikulyar uyğunluq müxtəlif həndəsi məsələlərin həllində, xüsusilə də oxşarlıq, paralellik, bərabərlik və bərabəryanlılıq məsələlərində geniş tətbiq tapır.
Uyğun tərəfləri perpendikulyar olan bucaqların gündəlik həyatda tətbiqi
Perpendikulyar uyğunluq yalnız nəzəri riyaziyyat üçün deyil, həm də real həyat üçün böyük əhəmiyyət kəsb edir. Məsələn, mühəndislikdə binanın divarları və tavanı, yolların kəsişməsi, dəmir yolu relslərinin birləşməsi və ya konstruksiyaların dayanıqlılığı məhz uyğun tərəflərin perpendikulyarlığına əsaslanır.
Gündəlik həyatda rast gəldiyimiz stolların, oturacaqların, pəncərə çərçivələrinin, qapıların və digər obyektlərin düzgün və funksional olması üçün, onların uyğun tərəfləri mütləq perpendikulyar olmalıdır. Bu, həm də estetik baxımdan səliqəli və gözəl görünüş formalaşdırır. Memarlıqda isə bu prinsip binanın möhkəmliyini və təhlükəsizliyini təmin edir.
Həndəsi fiqurlarda uyğun tərəfləri perpendikulyar olan bucaqlar
Ən çox rast gəlinən həndəsi fiqurlar arasında kvadrat və düzbucaqlı xüsusi yer tutur. Bu fiqurların bütün daxili bucaqları perpendikulyardır və uyğun tərəfləri bir-birinə qarşı 90° təşkil edir. Düzbucaqlı paralelopiped və kubda isə eyni zamanda üç ölçüdə perpendikulyar uyğunluq müşahidə olunur.
Cədvəl – Həndəsi fiqurlarda uyğun tərəfləri perpendikulyar olan bucaqlar
| Fiqur | Daxili bucaq (dərəcə) | Uyğun tərəflər | Perpendikulyarlıq |
|---|---|---|---|
| Kvadrat | 90 | Bütün tərəflər | Həmişə |
| Düzbucaqlı | 90 | Qarşı tərəflər | Həmişə |
| Kub | 90 | 3 ölçüdə | Həmişə |
| Düzbucaqlı prizmə | 90 | Qarşı/yan tərəflər | Həmişə |
| Parallelogram | 90 (bəzən) | Qarşı tərəflər | Nadir halda |
Perpendikulyarlıq və vektorlar
Vektorlar və onların qarşılıqlı vəziyyəti müasir riyaziyyatın və fizikanın əsas istiqamətlərindən biridir. İki vektorun uyğun komponentləri perpendikulyar olduqda, bu, onların skalyar hasilinin sıfıra bərabər olmasına gətirib çıxarır. Bu xüsusiyyət, həm koordinat müstəvisində, həm də üçölçülü fəza modellərində tətbiq olunur.
Vektorların perpendikulyarlığı, xüsusən də mexanika, mühəndislik və riyazi analizin müxtəlif sahələrində istifadə edilir. İki vektorun uyğun tərəflərinin perpendikulyar olmasını aşağıdakı kimi təsvir etmək mümkündür:
Əgər vektorlar a⃗a və b⃗b perpendikulyardırsa, onda onların skalyar hasili belə yazılır:
a⃗⋅b⃗=0a⋅b=0
Bu xüsusiyyət vasitəsilə həndəsi fiqurlarda da uyğun tərəflərin perpendikulyar olmasını yoxlamaq mümkündür.
Riyaziyyatda uyğun tərəflərin perpendikulyarlığı ilə bağlı fundamental teoremlər
Uyğun tərəfləri perpendikulyar olan bucaqlarla bağlı bir neçə mühüm teorem mövcuddur. Məsələn, Pifaqor teoremi və Taleqan teoremi bu münasibətlərin əsasını təşkil edir. Xüsusilə düzbucaqlı üçbucaqda uyğun katetlərin perpendikulyar olması, hipotenusun uzunluğunun hesablanmasında istifadə edilir.
Pifaqor teoremi:
Düzbucaqlı üçbucaqda uyğun tərəflər – katetlər – perpendikulyardır və onların kvadratları cəminin hipotenusun kvadratına bərabər olması bucaqların perpendikulyarlığını əyani şəkildə təsdiqləyir.
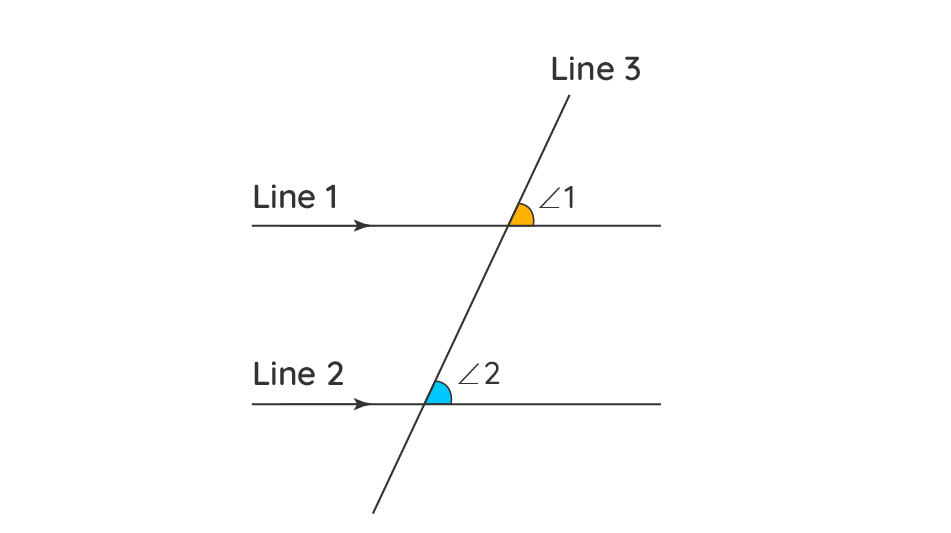
Taleqan teoremi:
İki paralel xəttə bir üçüncü xəttin perpendikulyar olması zamanı formalaşan bucaqlar arasında uyğunluq yaranır və onların qarşılıqlı yerləşməsi barədə nəticə çıxarmaq mümkün olur.
Uyğun tərəfləri perpendikulyar olan bucaqların öyrənilməsinin aktuallığı
Müasir təhsildə, xüsusən də riyaziyyat və fizika fənlərinin tədrisində bu anlayışların dərindən öyrənilməsi gələcək nəsillər üçün fundamental əhəmiyyət kəsb edir. Şagird və tələbələr bu konsepsiyanı tam mənimsədikdə, yalnız nəzəriyyə deyil, həm də praktik tətbiqlərdə – məsələn, qrafik dizayn, memarlıq, mexanika və digər sahələrdə uğur əldə edirlər. Perpendikulyar uyğunluq həm də məntiqi və analitik təfəkkürün inkişafında mühüm rol oynayır.
Uyğun tərəfləri perpendikulyar olan bucaqların gələcək tədqiqat perspektivləri
Elm və texnologiyanın inkişafı ilə paralel, bu konsepsiya yeni sahələrdə də tətbiq olunmaqdadır. Məsələn, kompüter qrafikasında 3D modelləşdirmədə, robot texnikasında, müasir inşaat və sənaye texnologiyalarında uyğun tərəflərin perpendikulyarlığı əsasında yeni metod və yanaşmalar formalaşır. Bu istiqamətdə aparılan tədqiqatlar riyaziyyatın praktiki və nəzəri əhəmiyyətini bir daha göstərir.
Uyğun tərəfləri perpendikulyar olan bucaqlar həm nəzəri riyaziyyatda, həm də gündəlik həyatda böyük əhəmiyyət kəsb edir. Bu anlayış, müxtəlif fiqurların xüsusiyyətlərinin düzgün başa düşülməsi, ölçülərin və məkanın dəqiq təsviri, alət və qurğuların etibarlılığı baxımından vacibdir. Riyazi analiz, həndəsi transformasiyalar və müxtəlif tətbiqi sahələrdə perpendikulyar uyğunluq prinsipi həm sabitlik, həm də funksionallıq yaradır. Bu mövzuya dərindən yiyələnmək, həm nəzəri biliyin zənginləşməsinə, həm də praktiki bacarıqların inkişafına böyük töhfə verir.
Ən Çox Verilən Suallar
Bu, iki və ya daha çox həndəsi fiqurun uyğun tərəflərinin bir-birinə 90 dərəcə bucaq altında yerləşməsi deməkdir. Bu münasibət fiqurlar arasında xüsusi riyazi və həndəsi əlaqənin olduğunu göstərir.
Kvadrat, düzbucaqlı, kub, düzbucaqlı prizmə və düzbucaqlı üçbucaqlarda bu xüsusiyyət daimi müşahidə olunur. Bu fiqurların bütün uyğun tərəfləri bir-birinə perpendikulyardır.
Memarlıqda, texniki konstruksiyalarda, mühəndislikdə, interyer dizaynında və bir çox alət və qurğunun düzəldilməsində uyğun tərəflərin perpendikulyarlığı əsas prinsip kimi tətbiq edilir.
Oxşarlıq, paralellik, simmetriya, bərabəryanlılıq, transformasiya və analitik hesablama məsələlərində uyğun tərəflərin perpendikulyarlığı vacib rol oynayır.
İki vektor və ya düz xəttin perpendikulyar olması onların skalyar hasilinin sıfır olmasına əsaslanır: a · b = 0.
3D modelləşdirmədə, robot texnikasında, sənaye dizaynında və proqramlaşdırmada perpendikulyar uyğunluq obyektlərin düzgün qurulmasını təmin edir.
Bu anlayışın tədrisi məkan təfəkkürünün inkişafına, riyazi biliklərin və analitik bacarıqların artırılmasına səbəb olur.
Bəzən yanlış olaraq hesab edilir ki, yalnız bir küncdə tərəflərin perpendikulyar olması bütün fiqura aid edilir. Əslində isə bütün uyğun tərəflərin yoxlanması vacibdir.
Pifaqor və Taleqan teoremləri bu sahədə ən fundamental riyazi nəticələr kimi qəbul olunur.
Yeni texnologiyaların inkişafı ilə bu anlayışın tətbiqi sahələri artır və fərqli elmi istiqamətlərdə yeni nəticələr əldə olunur.