Geometriyada əsas anlayışlardan biri üçbucaqlardır. Üçbucaq sadə fiqur kimi görünməsinə baxmayaraq, onun təbiətdə, riyaziyyatda, memarlıqda və gündəlik həyatda rolu misilsizdir. Hər bir üçbucaq üç düz xətt parçasından (tərəfdən) və bu tərəflərin kəsişmə nöqtələrində yerləşən üç bucaqdan ibarət qapalı həndəsi fiqurdur. Üçbucaqların əsrlər boyu riyazi və elmi düşüncənin əsas fiqurlarından birinə çevrilməsi təsadüfi deyil: onun unikallığı, sabitliyi, asanlıqla təsvir və təhlil olunması, praktiki tətbiq imkanları üçbucağı universallaşdırıb.
Üçbucaqlar yalnız məktəb riyaziyyatında deyil, təbiətdə, mühəndislikdə, texnologiyada və hətta incəsənətdə də vacib element kimi istifadə olunur. İnsanın ilk tanış olduğu riyazi formalardan biri məhz üçbucaqdır və onun mahiyyətini öyrənmək insanın məntiqi və yaradıcı təfəkkürünü inkişaf etdirir.
Üçbucağın tarixi və elmdəki rolu
Üçbucaqların tədqiqi qədim Misir, Babilistan və Yunanıstan elminə gedib çıxır. Ən qədim üçbucaqlı strukturlar piramidalarda, qədim tikililərdə və dekorativ sənətdə geniş istifadə olunub. Qədim yunan filosofu və riyaziyyatçısı Evklid özünün “Elementlər” əsərində üçbucaqların əsas xassələrini, növlərini və teoremlərini elmi cəhətdən təsbit edib. Pisagor teoremi və onun ümumiləşdirilmiş formaları üçbucaqların tədqiqində mühüm dönüş nöqtəsi olub.
Elmi inqilab dövründə üçbucaqlar, xüsusilə trigonometriya və analitik həndəsənin inkişafında əsas rol oynayıb. Triqonometriya elmi üçbucaqlar üzərində qurulub və bu sahədə Sinus, Kosinus və Tangens kimi anlayışlar üçbucaqların bucaqları və tərəfləri arasındakı münasibətləri riyazi cəhətdən dəqiq təsvir etməyə imkan verib.
Üçbucağın riyazi tərifi və əsas xassələri
Üçbucaq – bir müstəvidə yerləşən və ardıcıl olaraq birləşən üç nöqtə və bu nöqtələri birləşdirən üç xətt parçasından ibarət həndəsi fiqurdur. Üçbucağın tərəflərinə “a”, “b”, “c”, bucaqlarına isə “A”, “B”, “C” deyilir. Üçbucağın əsas xassələrindən biri onun daxil bucaqlarının cəminin həmişə 180° (dərəcə) olmasıdır. Yəni, istənilən üçbucağın hər üç daxil bucağını topladıqda cavab 180°-ə bərabər olur. Bu, yalnız müstəvi həndəsəsində doğrudur. Sferik və hiperbolik həndəsələrdə isə bu cəm dəyişir.
Üçbucağın perimetri tərəflərin cəminə, sahəsi isə müxtəlif düsturlarla (məsələn, Heron düsturu) hesablanır. Ən məşhur düsturlardan biri Heron düsturudur:
S = √[p(p-a)(p-b)(p-c)]Burada S – sahə, p – yarımpərimetr, a, b, c – üçbucağın tərəfləridir.
Üçbucaqların növləri və təsnifatı
Üçbucaqlar tərəflərinə və bucaqlarına görə bir neçə əsas növə ayrılır:
1. Bucaqlarına görə:
- Kəskinbucaqlı üçbucaq: Bütün bucaqları 90°-dən kiçikdir.
- Düzbucaqlı üçbucaq: Bir bucağı 90°-dir (düz bucaq), digər iki bucaq kəskindir.
- Korbuçaqlı üçbucaq: Bir bucağı 90°-dən böyükdür (kor bucaq).
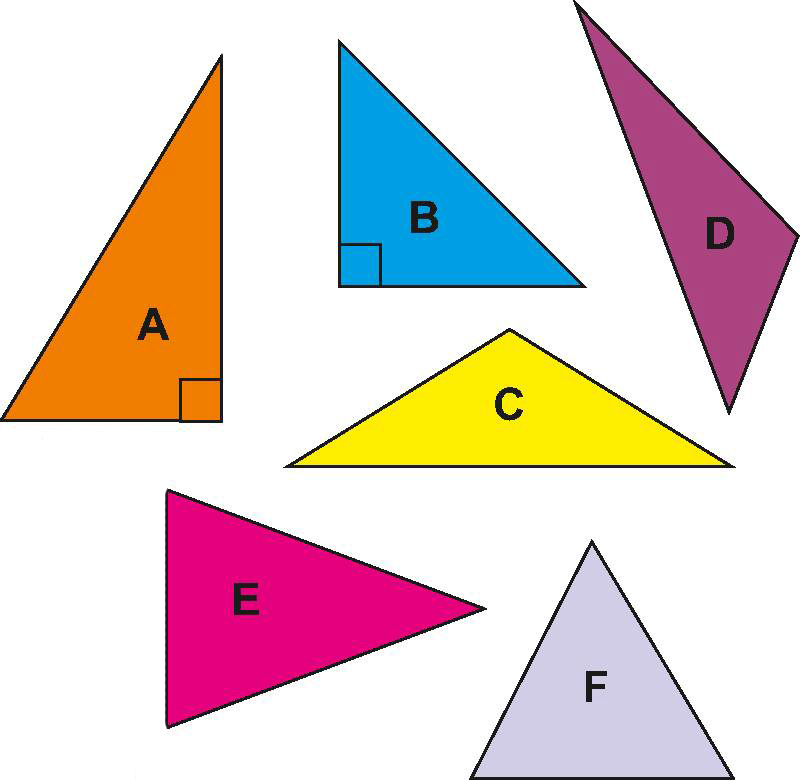
2. Tərəflərinə görə:
- Bərabəryanlı üçbucaq: İki tərəfi və bu tərəflərin qarşısındakı bucaqları bərabərdir.
- Bərabərtərəfli üçbucaq: Bütün tərəfləri və bucaqları bərabərdir (hər biri 60°).
- Müxtəlifyanlı üçbucaq: Bütün tərəfləri və bucaqları fərqlidir.
Bu təsnifat üçbucaqların müxtəlif teorem və xassələrinin öyrədilməsində əsas baza rolunu oynayır.
Üçbucağın əsas elementləri
Üçbucağın əsas elementləri bunlardır:
- Tərəflər: a, b, c – üçbucağın düz xətt parçası olan yanlarıdır.
- Bucaqlar: A, B, C – tərəflərin kəsişmə nöqtələrində əmələ gələn bucaqlardır.
- Hündürlük: Bir tərəfdən onun qarşısındakı zirvəyə çəkilən perpendikulyar xəttdir.
- Median: Zirvədən qarşı tərəfin orta nöqtəsinə çəkilən xətt.
- Bölən: Zirvədən bucağı iki bərabər hissəyə bölən xətt.
Üçbucağın bu elementləri riyaziyyatda və texniki elmlərdə əsas analiz və hesablama vasitələridir.
Üçbucağın sahəsinin və perimetrinin hesablanması
Üçbucağın perimetri sadəcə üç tərəfin cəminə bərabərdir:
P = a + b + c
Sahənin hesablanması isə bir neçə üsulla mümkündür:
- Heron düsturu: S = √[p(p-a)(p-b)(p-c)]
- Hündürlük vasitəsilə: S = ½ × əsas tərəf × ona çəkilmiş hündürlük
- Sinus düsturu: S = ½ × a × b × sinC
Bu düsturlar müxtəlif praktiki və nəzəri məsələlərin həllində geniş istifadə olunur.
Üçbucaqlarda əsas teoremlər və riyazi qanunlar
Üçbucaqlarla bağlı ən mühüm teoremlər bunlardır:
- Pisagor teoremi: Düzbucaqlı üçbucaqlarda katetlərin kvadratlarının cəmi hipotenuzanın kvadratına bərabərdir.
- Sinuslar teoremi: Hər hansı üçbucağın tərəfinin və ona qarşı bucağın sinusunun nisbəti sabitdir.
- Kosinuslar teoremi: Hər hansı üçbucağın tərəfinin kvadratı digər iki tərəfin kvadratları və aralarındakı bucağın kosinusu ilə ifadə olunur.
- Büdcələr cəmi: Hər üç bucağın cəmi 180°-dir.
Bu teoremlər məktəb riyaziyyatının, eləcə də mühəndislik və texniki sahələrin əsasıdır.
Üçbucaqların gündəlik həyatda və təbiətdə rolu
Üçbucaq təbiətdə ən sabit, dayanıqlı və praktik fiqurlardan biridir. Mühəndislikdə və memarlıqda körpü, qüllə və böyük tikililərdə dayanıqlığı təmin edən məhz üçbucaqlı konstruksiyalardır. Təbiətdə isə bir çox canlıların skelet quruluşunda, bitki və mineral formalarında, kristallarda üçbucaq və onun variasiyaları rast gəlinir.
Bundan əlavə, incəsənətdə kompozisiya və vizual balans yaratmaq üçün üçbucaqlar tez-tez istifadə olunur. Rəssamlıqda, qrafik dizaynda, hətta fotoqrafiyada üçbucaq kompozisiyanın əsas strukturlarından biri kimi çıxış edir.
Üçbucaqların informatika və texnologiyada tətbiqi
Müasir kompüter qrafikasında, üçölçülü modelləşdirmədə üçbucaqlar əsas tərtibat və vizualizasiya elementi kimi istifadə olunur. Hər hansı 3D model əsasən üçbucaqlardan ibarət “mesh” strukturu ilə qurulur. Kompüter oyunlarında və animasiyada, virtual reallıq sistemlərində, geoinformasiya texnologiyalarında üçbucaqlar əsas məlumat vahidi və hesablamaların bazasıdır.
Azərbaycan təhsilində üçbucaqların öyrədilməsi
Azərbaycan məktəblərində üçbucaqlar həndəsənin əsas bölmələrindən biri kimi erkən yaşlardan tədris olunur. Müasir dərsliklərdə üçbucağın riyazi əsasları, tipologiyası, praktiki tətbiqi, klassik teoremlər və həyatla əlaqələri geniş şəkildə izah edilir. Şagirdlər üçbucaqlar vasitəsilə məntiqi düşünmə, problemlərin həllində riyazi alətlərin istifadəsini öyrənir, bu mövzu olimpiada və qəbul imtahanlarında əsas riyazi bölmə kimi yer alır.
Üçbucağın simvolik və mədəni mənası
Üçbucaq bir çox mədəniyyətlərdə simvolik məna daşıyır. Onun üç zirvəsi tez-tez vəhdət, güc, ailə, müqəddəslik və harmoniya anlayışları ilə assosiasiya olunur. Qədim xalqlarda üçbucaq müqəddəs forma sayılıb, bəzən ailə – ata, ana, uşaq vəhdətinin, bəzən yaradılış – keçmiş, bu gün, gələcək anlamının rəmzi olub. Müasir incəsənətdə, korporativ loqotiplərdə və dizaynda üçbucaqlar vizual olaraq dinamika, sabitlik və inkişaf mesajı verir.
Üçbucaqlar – riyaziyyatın, təbiətin, memarlığın və mədəniyyətin ayrılmaz parçasıdır. Onun forması, xassələri, simvolik və praktik əhəmiyyəti insan düşüncəsinin, elmin və incəsənətin inkişafına xidmət edib və etməkdədir. Üçbucağın sadəliyi arxasında böyük sabitlik, funksionallıq və dərin mənalar gizlənir. Müasir elmdə, gündəlik həyatda və milli təhsil sistemində üçbucağın yeri həmişə aktual və dəyərlidir.
Ən Çox Verilən Suallar
Üçbucaq – üç tərəfi və üç bucağı olan, əsas xassəsi daxil bucaqlarının cəminin 180° olması olan müstəvi fiqurdur.
Bucaqlarına görə kəskinbucaqlı, düzbuçaqlı və korbuçaqlı; tərəflərinə görə bərabəryanlı, bərabərtərəfli və müxtəlifyanlı üçbucaqlar var.
Ən məşhur düstur Heron düsturudur: S = √[p(p-a)(p-b)(p-c)] və ya S = ½ × əsas × hündürlük.
Perimetr bütün tərəflərin cəminə bərabərdir: P = a + b + c.
Pisagor teoremi düzbuçaqlı üçbucaqlarda tərəflər arasındakı əlaqəni izah edir və mühəndislikdə əsas alətlərdən biridir.
Mühəndislikdə, memarlıqda, təbiətdə, kompüter qrafikasında və dizaynda.
Qədim Misir, Babil və Yunanıstan riyaziyyatında, klassik elmlərdə üçbucaqlar əsas tədqiqat obyekti olub.
Üçbucaq güc, vəhdət, ailə və harmoniya kimi simvolik məna daşıyır.
Tərəflər, bucaqlar, hündürlük, median, bölən üçbucağın əsas elementləridir.
Riyazi təfəkkürün, məntiqi düşünmənin, analitik bacarıqların formalaşması və gündəlik həyat problemlərinin həlli üçün.