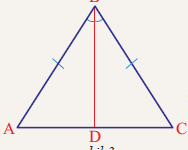
Həndəsə və riyaziyyatda “üçbucaq bərabərsizliyi” ən fundamental və universal qaydalardan biridir. Bu prinsip yalnız məktəb riyaziyyatı və klassik həndəsədə deyil, analitik həndəsə, cəbr, funksional analiz, optimallaşdırma, fizika və hətta real həyat problemlərinin həllində geniş istifadə olunur. Üçbucaq bərabərsizliyi üç nöqtənin bir-birinə olan məsafələri və onların arasındakı münasibəti təsvir edir. Hər bir üçbucaq üçün, onun istənilən iki tərəfinin cəmi üçüncü tərəfdən böyük, fərqi isə üçüncü tərəfdən kiçik olmalıdır. Məhz bu qayda üçbucağın həndəsi mövcudluğunu və sabitliyini təmin edir.
Bu bərabərsizlik həm klassik həndəsənin, həm də riyazi məntiq və fizikanın təməl prinsiplərindən hesab olunur. Onun başa düşülməsi və tətbiqi riyaziyyatın bir çox sahəsində, eləcə də mühəndislik və texniki elmlərdə əsas rol oynayır.
Üçbucaq bərabərsizliyinin elmi və tarixi kökləri
Üçbucaq bərabərsizliyinin elmi kökləri qədim yunan həndəsəsinə, xüsusilə Evklid və Arximed kimi riyaziyyatçıların əsərlərinə dayanır. Qədim yunanlar üçbucağın mövcudluq şərtlərini və tərəflər arasındakı münasibətləri ilk dəfə ciddi şəkildə analiz etmiş, bunun nəticəsində bərabərsizlik prinsipi formalaşıb.
XIX əsrdə bu prinsip yalnız həndəsi müstəvidə deyil, həm də cəbrdə və analitik mühitlərdə ümumiləşdirilib. Triqonometriyada, vektor analizində, normlu məkanlarda (məsələn, Euklid məkanı, funksional analizdəki Banax və Hilbert məkanları) üçbucaq bərabərsizliyi əsas aksiomlardan birinə çevrilib.
Üçbucaq bərabərsizliyinin riyazi ifadəsi
Riyaziyyatda üçbucaq bərabərsizliyi klassik formada belə ifadə olunur:
Hər hansı bir üçbucağın istənilən iki tərəfinin cəmi üçüncü tərəfdən böyük olmalıdır.
Əgər a, b, c üçbucağın tərəfləridirsə, onda həmişə aşağıdakı bərabərsizliklər ödənir:
a + b > c
a + c > b
b + c > a
Bundan əlavə, istənilən iki tərəfin fərqi üçüncü tərəfdən kiçik olmalıdır:
|a – b| < c
|a – c| < b
|b – c| < a
Bu bərabərsizliyin ödənilməsi üçbucağın müstəvidə qurulması və onun sabitliyi üçün zəruridir.
Üçbucaq bərabərsizliyinin həndəsi mənası
Üçbucaq bərabərsizliyi göstərir ki, bir nöqtədən digər iki nöqtəyə ən qısa yol həmişə birbaşa düz xəttdir. Əgər iki nöqtə arasındakı yol başqa bir üçüncü nöqtədən keçərsə, bu yol hər zaman birbaşa məsafədən böyük olacaq. Bu prinsip istənilən müstəvidə, hətta qeyri-Evklid həndəsələrində və yüksəkölçülü fəzada da öz əhəmiyyətini qoruyur.
Bu bərabərsizlik intuitiv olaraq izah edir ki, heç vaxt bir üçbucağın iki tərəfinin cəmi üçüncü tərəfə bərabər və ya ondan kiçik ola bilməz, əks halda belə bir üçbucaq mövcud olmur, yəni nöqtələr düz xəttdə yerləşir və fiqur degenarativ olur.
Üçbucaq bərabərsizliyinin analitik tətbiqləri
Üçbucaq bərabərsizliyi yalnız həndəsə ilə məhdudlaşmır. Analitik həndəsədə vektorların uzunluqları və aralarındakı məsafələr də bu prinsipə tabe olur.
Məsələn, istənilən iki vektorun uzunluqlarının cəmi, onların fərqinin uzunluğundan böyükdür:
|u + v| ≤ |u| + |v|
Bu bərabərsizlik normlu məkanlarda, o cümlədən funksional analiz və kompleks analizdə əsas aksiomlardan biridir. Xüsusilə Banax və Hilbert məkanlarında üçbucaq bərabərsizliyi olmadan heç bir struktur və ölçü anlayışı qurmaq mümkün deyil.
Üçbucaq bərabərsizliyinin gündəlik həyatda rolu
Praktiki həyatda da üçbucaq bərabərsizliyinin prinsipi bir çox sahədə tətbiq edilir: məsələn, nəqliyyat logistikası, rabitə, tikinti və mühəndislik layihələrində optimal məsafə və resursların bölgüsündə. Məsələn, üç məntəqə arasında ən səmərəli yolun seçilməsi üçün məhz bu prinsipdən istifadə olunur. GPS sistemləri, kartoqrafiya, aviasiya və dənizçilikdə də üçbucaq bərabərsizliyi fundamental rol oynayır.
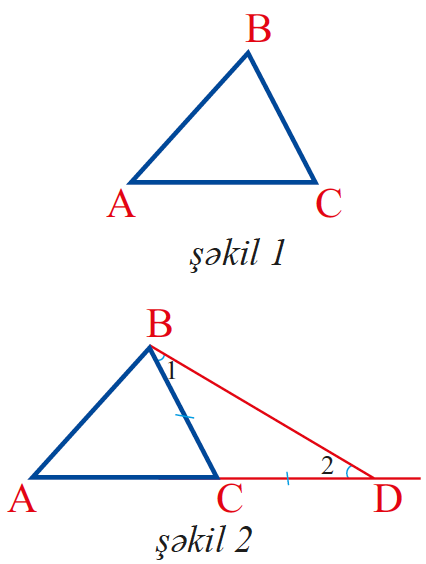
Üçbucaq bərabərsizliyi və riyazi sübutlar
Üçbucaq bərabərsizliyi riyaziyyatda çoxsaylı sübut və tətbiqlərə malikdir. Bu bərabərsizliklərin sübutu üçün müxtəlif həndəsi, analitik və cəbri üsullardan istifadə olunur. Məsələn, həndəsi sübutda paralelqonun diaqonalına əsaslanır, analitik sübut isə vektorların koordinat təhlili ilə aparılır.
Qeyd etmək lazımdır ki, üçbucaq bərabərsizliyi riyazi məntiqin bir çox mühüm nəticələrinin və teoremlərin (məsələn, Minkovski bərabərsizliyi, Hölder bərabərsizliyi və s.) əsasını təşkil edir.
Üçbucaq bərabərsizliyinin pozulması və mümkün nəticələr
Əgər üçbucaq bərabərsizliyi pozularsa, yəni istənilən iki tərəfin cəmi üçüncü tərəfə bərabər və ya ondan kiçik olarsa, həmin nöqtələr düz xətt üzərində yerləşir və üçbucaq deyil, düz xətt parçası əmələ gəlir. Bu, həm həndəsə, həm də real həyat problemlərində sabitliyin pozulması, optimal həllərin olmaması və ya qeyri-mümkünlüyü ilə nəticələnir. Bu səbəbdən üçbucaq bərabərsizliyi real və nəzəri strukturların qurulmasında vacib meyardır.
Üçbucaq bərabərsizliyinin genişlənmələri və digər sahələrə təsiri
Riyaziyyatın digər bölmələrində (məsələn, kompleks ədədlər, vektor analiz, funksional analiz) üçbucaq bərabərsizliyi fərqli formalarda ifadə olunur. Ən ümumi formada normlu məkanlarda belə yazılır:
||x + y|| ≤ ||x|| + ||y||
Bu prinsip riyaziyyatda “metrik məkan” anlayışının tərifində əsas yer tutur və bütün məsafə, norm və ölçü anlayışlarının əsasıdır. Statistika, ehtimal nəzəriyyəsi, informasiya nəzəriyyəsində də üçbucaq bərabərsizliyi bənzər ideyalarla tətbiq edilir.
Azərbaycan təhsilində və olimpiadalarda üçbucaq bərabərsizliyi
Azərbaycan məktəblərində, riyaziyyat olimpiadalarında və ali məktəb proqramlarında üçbucaq bərabərsizliyi əsas mövzulardan biridir. Şagird və tələbələr bu prinsipin təməlini öyrənir, onun müxtəlif formalarda tətbiqini praktiki və nəzəri məsələlərdə istifadə edir. Olimpiada tapşırıqlarında üçbucaq bərabərsizliyinin məharətlə tətbiqi çox zaman ən qısa və düzgün həll yoludur.
Üçbucaq bərabərsizliyi həndəsənin, riyaziyyatın və praktiki elmlərin ən vacib prinsiplərindən biridir. Bu qayda olmadan üçbucağın və çoxsaylı riyazi strukturların mövcudluğu mümkün deyil. Həyatın müxtəlif sahələrində bu bərabərsizlik insanlara optimal həllər tapmaq, sabitlik və nizam yaratmaq, elmi yanaşma ilə problemləri həll etmək imkanı verir. Üçbucaq bərabərsizliyi, riyaziyyatın gözəlliyini və tətbiq imkanlarını açıq şəkildə nümayiş etdirən universal qanundur.
Ən Çox Verilən Suallar
Üçbucaq bərabərsizliyi – istənilən iki tərəfin cəminin üçüncü tərəfdən böyük, fərqinin isə üçüncü tərəfdən kiçik olmasıdır.
a + b > c; a + c > b; b + c > a, burada a, b, c üçbucağın tərəfləridir.
Çünki yalnız bu halda üçbucaq qurmaq, onun sabitliyini və həndəsi mövcudluğunu təmin etmək mümkündür.
Xeyr, bu prinsip cəbrdə, vektor analizində, funksional analizdə və metrik məkanlarda da əsasdır.
Bu halda üç nöqtə bir düz xətt üzərində yerləşir və üçbucaq deyil, düz xətt parçası yaranır.
Optimal yol seçimi, logistik planlama, rabitə və müxtəlif sahələrdə məsafələrin hesablanmasında istifadə olunur.
İki vektorun uzunluğunun cəmi onların cəminin uzunluğundan böyük və ya bərabərdir: |u + v| ≤ |u| + |v|.
Əsasən həndəsə və riyaziyyat dərslərində, olimpiada və praktiki məsələlərdə tətbiqi geniş şəkildə izah olunur.
Bəli, metrik, normlu məkanlarda və müxtəlif riyazi strukturlarda fərqli formalarda tətbiq edilir.
Üçbucaq və bir çox riyazi obyektlər mövcud olmur, sabitlik və optimal həll mümkün olmur.