Beşbucaqlı prizma çoxbucaqlılar həndəsəsində həm nəzəri baxımdan, həm də tətbiqi sahələrdə tez-tez qarşılaşılan həcm fiqurudur. İki paralel beşbucaqlı baza və onları birləşdirən beş yan üzdən ibarət olan bu prizma arxitektura, qablaşdırma, mexanika və hətta təhsil modellərində rahatlıqla istifadə olunur. Riyazi cəhətdən onun cəlbediciliyi sabit həcm düsturu ilə yanaşı səth sahəsinin çevik hesablanmasıdır: baza sahəsi və perimetr doğru seçildikdə, istənilən yüksəklikdə nəticə dəqiqliklə əldə edilir. Beşbucaqlı prizma simmetriya baxımından balanslıdır; müntəzəm beşbucaqlı baza seçildikdə hesablama sadələşir, vizual estetika güclənir. Sağ (dik) və maili variantların hər ikisində həcm baza sahəsinin hündürlüyə hasilinə bərabərdir, bu fakt konstruksiyalarda ölçülərin miqyaslandırılmasını asanlaşdırır. Laboratoriyada karton maketlərlə quruluşu nümayiş etdirmək, vektor yanaşması ilə koordinatlarda modelləşdirmək mümkündür. Gündəlik həyatda beşbucaqlı kəsimli sütun və modulların seçilməsi məkan qənaəti, fərqli estetika və yüklərin paylanmasında üstünlüklər gətirir. Mühəndislər üçün səth sahəsinin düzgün hesabı material sərfinin optimallaşdırılması deməkdir; müəllimlər üçün isə bu prizma çoxbucaqlı-baza anlayışını möhkəmləndirən əlverişli nümunədir. Şagirdlər perimetr, apotema və trigonometriya əlaqələrini burada praktik şəkildə birləşdirə bilirlər. Modelin üst-üstə düşən parametrləri – perimetrin hündürlüklə yaratdığı yan səth, apotemanın baza sahəsi ilə əlaqəsi – anlayışlararası körpü yaradır. Beşbucaqlı prizma ilə işləyərkən vahidlərin düzgün seçilməsi, yuvarlaqlaşdırma qaydalarına riayət və ölçmə səhvlərinin analizi də texniki savadın ayrılmaz hissəsidir.
Tərif və əsas anlayışlar
Beşbucaqlı prizma iki müvafiq, paralel beşbucaqlı bazadan və bu bazaların uyğun tərəflərini birləşdirən beş yan üzdən ibarətdir. Prizmanın “sağ” adlandırılması bütün yan üzlərin bazalara perpendikulyar olmasına işarədir; əks halda prizma “maili” sayılır. Üzlərin sayı 7-dir: 2 baza + 5 yan üz. Kənarların sayı 15, təpə nöqtələrinin sayı isə 10-dur. Müntəzəm beşbucaqlı baza seçildikdə bütün kənarlar eyni olur və çevrəvi simmetriya sadələşir.
Baza poliqonu qeyri-müntəzəm olduqda hələ də prizma sayılır, lakin sahə və perimetr hesabı çoxbucaqlının real ölçülərinə əsasən aparılmalıdır. Prizmanın hündürlüyü bazaların bir-birinə olan perpendikulyar məsafəsidir; maili prizmalarda kənarların uzunluğu hündürlükdən fərqli ola bilər. Yan üzlər sağ prizmada düzbucaqlı, maili prizmada isə paralelloqram şəklindədir.
Həndəsi parametrlər və əsas düsturlar
Həcm hər iki növdə eynidir: V=Ab⋅hV=Ab⋅h, burada AbAb baza sahəsi, hh isə hündürlükdür. Ümumi səth sahəsi S=2Ab+Pb⋅hS=2Ab+Pb⋅h kimi verilir; PbPb bazanın perimetridir. Sağ prizma üçün yan səth sahəsi Sy=Pb⋅hSy=Pb⋅h düzbucaqlıların cəmi olduğundan sadə alınır. Maili prizmalarda yan üzlər paralelloqram olduğundan, “h” yan üzlərin hündürlüyü deyil, bazalararası perpendikulyar məsafədir.
Müntəzəm beşbucağın sahəsi iki ekvivalent formulla hesablana bilər: Ab=5a24tan(36∘)Ab=4tan(36∘)5a2 və ya Ab=12Pb⋅raAb=21Pb⋅ra. Burada aa tərəf uzunluğu, Pb=5aPb=5a perimetr, ra=a2tan(36∘)ra=2tan(36∘)a isə apotemadır. Bu əlaqələr praktiki hesablamalarda çevik kombinasiya imkanı verir.
Koordinat və vektor yanaşması
Prizmanı koordinat sistemində modelləşdirərkən bazalardan birini z=0z=0, digərini z=hz=h müstəvisində yerləşdirmək hesablama prosesini xeyli sadələşdirir. Baza təpələrinin koordinatları dairə üzərində bərabər bucaqlı paylanma ilə generasiya edilə, beləliklə müntəzəm beşbucağın perimetr və sahəsi vektorlarla təsdiq edilə bilər. Vektorların xaç hasilindən istifadə etməklə poliqon sahəsi parçalanmış üçbucaqların cəmi kimi də tapılır.
Maili prizmanı təsvir etmək üçün ikinci bazanı vektor s⃗s qədər sürüşdürmək yetərlidir: üst baza təpələri ri⃗+s⃗ri+skimi alınır. Həcmin invariant qalması Gauss teoremi və ya həcmin bazaya proyeksiya sahəsi ilə hündürlüyün hasilinə bərabərliyi ilə əsaslandırılır. Belə modelləşdirmə CAD mühitlərində möhkəmlik, kütlə mərkəzi və səthlər üzrə məsafələrin avtomatik hesabına imkan verir.
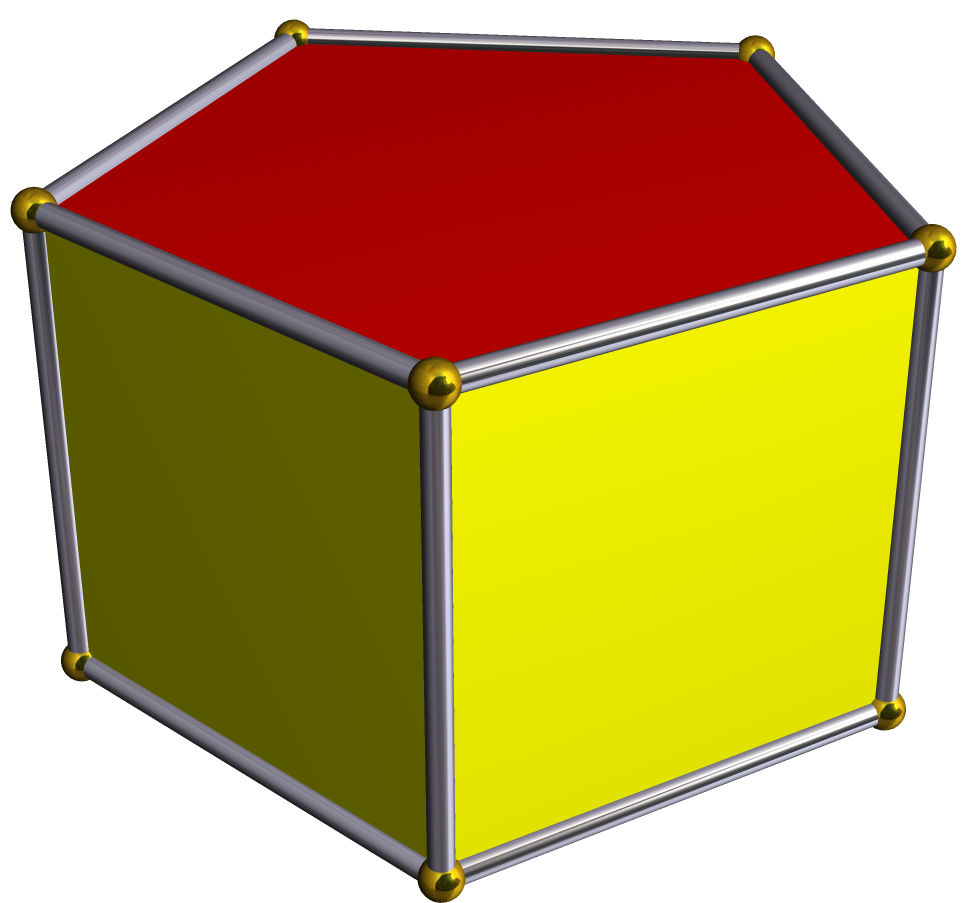
Ölçmə, vahidlər və tipik texniki tələblər
Həndəsi parametrlər SI vahidlərində ifadə olunmalıdır: uzunluq metr və ya santimetrdə, sahə kvadrat vahiddə, həcm kub vahiddə yazılır. Material kəsimi, qablaşdırma və 3D çap işlərində səth sahəsinin dəqiq hesabı sərfiyyata birbaşa təsir edir. Hesablamalarda yuvarlaqlaşdırma qaydasına (məsələn, iki və ya üç onluq) əvvəlcədən qərar vermək yekun nəticələrin müqayisəsini asanlaşdırır.
Tolerans məsələləri də önəmlidir: baza kənarlarında ±0,5 mm ölçü sapması, hündürlükdə ±1 mm sapma səth sahəsində yüzdəlik fərqlərə səbəb ola bilər. Məktəb laboratoriyalarında karton və ya köpük maketlərlə hazırlanmış modellərdə kənarların düzlüyünü qorumaq üçün kəsim bucaqları və yapışqan qatının qalınlığına nəzarət faydalıdır. Təcrübələrdə real ölçmə xətası ilə nəzəri dəyər arasındakı fərqi hesablamaq şagirdlərə səhv analizini öyrədir.
Praktik tətbiqlər və dizayn məqamları
Arxitektura və interyer dizaynında beşbucaqlı kəsimli sütun və işıqlandırma korpusları vizual monotonluğu azaldır, modul sistemlərdə ritm yaradır. Qablaşdırmada prizmatik qutular raflarda daha yaxşı sabitlik verir və daşınma zamanı mexaniki yükləri künclərə bərabər yayır. Mexaniki konstruksiyalarda prizmatik kirişlərin kəsiyi daşıyıcı qabiliyyət və əyilmə sərtliyi arasında balans yaratmaq üçün optimallaşdırılır.
Tədrisdə beşbucaqlı prizma çoxbucaqlıların sahəsi, apotema-perimetr əlaqəsi və həcm düsturlarının birgə tətbiqini modelləşdirir. Robototexnika və maker layihələrində lazer kəsimlə hazırlanan prizmatik karkaslar yüngül, lakin sərt konstruksiya təqdim edir. Rəqəmsal istehsalda “unfold” (səth açılımı) əməliyyatı ilə yan səthin düzbucaqlı zolaq kimi plana keçirilməsi kəsim xəritələrinin hazırlanmasını asanlaşdırır.
Hesablama nümunəsi: müntəzəm baza, sağ prizma
Tutaq ki, prizmanın müntəzəm baza tərəfi a=6 sma=6sm, hündürlüyü h=12 smh=12sm-dir. Perimetr Pb=5a=30 smPb=5a=30sm. Apotema ra=a2tan36∘≈62⋅0,7265≈4,132 smra=2tan36∘a≈2⋅0,72656≈4,132sm. Baza sahəsi Ab=12Pbra≈0,5⋅30⋅4,132≈61,98 sm2Ab=21Pbra≈0,5⋅30⋅4,132≈61,98sm2. Alternativ olaraq Ab=5a24tan36∘Ab=4tan36∘5a2 ilə eyni nəticə alınır.
Həcm V=Ab⋅h≈61,98⋅12≈743,76 sm3V=Ab⋅h≈61,98⋅12≈743,76sm3. Yan səth sahəsi Sy=Pb⋅h=30⋅12=360 sm2Sy=Pb⋅h=30⋅12=360sm2. Ümumi səth sahəsi S=2Ab+Sy≈2⋅61,98+360≈483,96 sm2S=2Ab+Sy≈2⋅61,98+360≈483,96sm2. Dəyərlər texniki tələbdən asılı olaraq, məsələn, iki onluq dəqiqliklə təqdim oluna bilər. Bu nümunə kiçik ölçülü dekorativ korpusun material sərfini proqnozlaşdırmağa imkan verir.
Sağ və maili prizma: fərqlər, oxşarlıqlar
Sağ prizmada yan üzlər bazalara perpendikulyar yerləşdiyi üçün hər yan üz düzbucaqlıdır və səth sahəsi hesabatı xeyli sadələşir. Maili prizmada yan üzlər paralelloqramdır; lakin həcm yenə baza sahəsi ilə bazalararası perpendikulyar məsafənin hasilinə bərabər qalır. Bu, Cavalieri prinsipinin xüsusi halı kimi başa düşülə bilər: bazalar paralel, kəsik sahələri bərabər olduqda həcm bərabər olur.
Konstruktiv baxımdan sağ prizmalar montaj və kəsim xəritələrində daha rahatdır. Maili prizma isə estetik məqsədlərlə, aerodinamik və ya ergonomik səbəblərlə seçilə bilər. Lakin maililik artdıqca yan örtük panellərinin ölçüləri fərqlənir, bu da istehsal planında əlavə ölçüləndirmə tələb edir.
Cədvəl: Variantların müqayisəsi
| Parametr | Sağ, müntəzəm bazalı | Maili, müntəzəm bazalı | Qeyri-müntəzəm baza |
|---|---|---|---|
| Həcm | Ab⋅hAb⋅h | Ab⋅hAb⋅h | Ab⋅hAb⋅h |
| Yan səth | Pb⋅hPb⋅h | Paralelloqramların cəmi, ümumən Pb⋅hPb⋅h | Baza perimetri əsasında |
| Ümumi səth | 2Ab+Pbh2Ab+Pbh | 2Ab+Pbh2Ab+Pbh | 2Ab+Pbh2Ab+Pbh |
| Üz forması | Düzbucaqlar | Paralelloqramlar | Qarışıq |
| İstehsal asanlığı | Yüksək | Orta | Ölçülərdən asılı |
Səth açılımı və material planlaması
Yan səth açıldıqda uzunluğu perimetrə, hündürlüyü prizma hündürlüyünə bərabər olan düzbucaqlı alınır. Bu açılım, metal və ya karton təbəqədən kəsim xəritəsi hazırlayarkən materialdan rasional istifadəni təmin edir. Kənar birləşdirmələr üçün 5–10 mm-lik əlavə pay qoymaq montajda möhkəmliyi artırır. Baza panelləri üçün isə ayrıca beşbucaqlar kəsilir və yan zolağa bərkidilir.
3D çapda dilimləmə proqramları səth açılımına ehtiyac duymur, lakin səth sahəsi məlumatı material sərfini təxmini hesablamağa yardım edir. Boyama və ya örtük tətbiqlərində səth sahəsinin dəqiq hesablanması (məsələn, kvadrat metrə düşən boya sərfi) xərc planlamasını optimallaşdırır. Daxili sərtləndirici çıta və ya kənar profillər əlavə edilərsə, kütlə artımı və səth sahəsi yenidən qiymətləndirilir.
Məşq tapşırıqları və didaktik məsləhətlər
Tədrisdə əvvəlcə müntəzəm baza ilə başlanıb, sonra qeyri-müntəzəm bazalara keçmək məsləhətdir. Şagirdlərə eyni perimetrə malik müxtəlif beşbucaqların sahəsini müqayisə etdirmək apotema-perimetr əlaqəsini dərinləşdirir. Maili prizmanın həcminin dəyişməməsini göstərmək üçün eyni baza və hündürlüyə malik sağ prizma ilə kəsik sahələrinin bərabərliyini müşahidə etdirmək faydalıdır.
Hesablamalarda səhv mənbələri kimi vahid qarışıqlığı, bucaq funksiyalarında dərəcə–radian çevirməsini və yuvarlaqlaşdırmanı müzakirə edin. Modelləşdirmədə karton zolağı perimetr uzunluğunda kəsib hündürlüyü qədər qaldırmaq prizmanın “təbiətini” hiss etdirir. Qrafik kalkulyator və ya cədvəllərlə tan36∘tan36∘ dəyərinin düzgün götürülməsi baza sahəsində dəqiqliyi artırır.
Beşbucaqlı prizma müntəzəm çoxbucaqlıların həcm fiqurları içində təsirli öyrənmə və tətbiq nümunəsi təqdim edir. Onun quruluşu sadə olsa da, sahə–perimetr–apotema əlaqəsi kimi bir neçə əsas anlayışı eyni anda işlətməyi tələb edir. Həcm düsturunun sadəliyi ölçülərin miqyaslandırılmasını və layihələrin material hesabını rahatlaşdırır. Sağ və maili variantların müqayisəsi şagirdlərə həndəsədə invariant anlayışını intuitiv göstərir. Səth açılımı və yan səthin perimetr-hündürlük düzbucaqlısı şəklində təmsili istehsalda real dəyərə malikdir. Müntəzəm baza seçildikdə trigonometriya ilə əlaqə güclənir, qeyri-müntəzəm bazada isə koordinat həndəsəsi və poliqon sahəsi alqoritmləri ön plana çıxır. Praktik nümunələr, o cümlədən 3D çap və karton modellər, anlayışı konkretləşdirir. Tolerans və ölçmə səhvlərinin təhlili texniki düşüncəni inkişaf etdirir. Rəqəmsal dizaynda bu prizma modul konstruksiyalara estetik və funksional alternativ yaradır. Mexaniki baxımdan, kəsik seçimi daşıyıcı qabiliyyətə və sərtliyə təsiri baxımından maraqlı təhlil predmetidir. Beşbucaqlı prizma üzərində işləmək həm riyazi zövqü, həm də praktiki bacarıqları birləşdirir. Düzgün metodologiya ilə o, tədrisdə və mühəndislikdə dayanıqlı alətə çevrilir. Geniş tətbiq spektri onun həndəsə kurikulumlarında uzunmüddətli yerini əsaslandırır.
Ən Çox Verilən Suallar
Beşbucaqlı prizma iki paralel beşbucaqlı baza və onları birləşdirən beş yan üzdən ibarət həcm fiqurudur. Üzlərin ümumi sayı 7-dir: 2 baza və 5 yan üz. Kənarların sayı 15, təpələrin sayı isə 10 olur. Sağ prizmada yan üzlər bazalara perpendikulyardır, maili prizmada isə paralelloqram şəklində formalaşır.
Həcm düsturu hər iki tip (sağ və maili) üçün eynidir: V = A_b · h. Burada A_b baza sahəsi, h isə bazalar arasındakı perpendikulyar məsafədir. Baza sahəsi dəqiq tapıldıqda həcmi hesablamaq sadə hasilə enir. Bu xüsusiyyət konstruktiv dizaynda ölçülərin miqyaslandırılmasını asanlaşdırır.
Ümumi səth sahəsi S = 2A_b + P_b · h düsturu ilə hesablanır. P_b bazanın perimetridir, h prizmanın hündürlüyüdür. Sağ prizmada yan səth P_b · h düzbucaqlı zolağa bərabərdir. Maili prizmada da eyni ifadə keçərlidir, çünki yan üzlərin ümumi hündürlüyü perimetr üzrə h qədər proyeksiya verir.
İki əsas formula var: A_b = (5a^2)/(4·tan36°) və A_b = (1/2)·P_b·r_a. Burada a tərəf uzunluğu, P_b = 5a perimetr, r_a isə apotemadır: r_a = a/[2·tan(36°)]. Hər iki formula eyni nəticəni verir, seçim praktiki rahatlığa bağlıdır. Trigonometriya cədvəllərindən doğru dəyərləri götürmək dəqiqlik üçün vacibdir.
Sağ prizmada yan üzlərin hamısı bazalara perpendikulyardır və düzbucaqlıdır. Maili prizmada yan üzlər paralelloqram olur və kənarların istiqaməti hündürlüklə üst-üstə düşməyə bilər. Buna baxmayaraq həcmin düsturu dəyişmir: A_b · h. Səth açılımı və istehsal planı isə sağ prizmada daha sadədir.
Yan səth açıldıqda perimetr uzunluğunda və hündürlük enində düzbucaqlı alınır. Bu zolağa iki beşbucaqlı baza paneli əlavə olunmaqla tam açılım xəritəsi əldə edilir. Açılım material kəsimində sərfiyyatı planlaşdırmağa imkan verir. Qatlama payları üçün əlavə 5–10 mm nəzərdə saxlamaq montajda rahatlıq yaradır.
Əvvəlcə bazanın perimetri və apotemasını müəyyənləşdirin. Sahəni ya (1/2)·P_b·r_a, ya da (5a^2)/(4·tan36°) ilə tapın. Sonra h ilə vuraraq həcmi, P_b·h ilə yan səthi, 2A_b əlavə etməklə ümumi səthi hesablayın. Nəticələri seçilmiş yuvarlaqlaşdırma qaydasına görə təqdim edin.
Belə halda baza sahəsi çoxbucaqlının real təpə koordinatlarına və ya parçalanmış üçbucaqların sahələrinin cəminə görə hesablanır. Perimetr də ayrı-ayrı tərəflərin cəmi kimi götürülür. Düsturlar S = 2A_b + P_b·h və V = A_b·h eyni qalır. Yeganə fərq A_b və P_b-nin tapılma yolundadır.
Xeyr, maili prizmalarda kənar uzunluğu prizmanın hündürlüyündən böyük ola bilər. Hündürlük bazalar arasındakı perpendikulyar məsafədir. Hesablarda həmişə bu perpendikulyar məsafədən istifadə edilməlidir. Sağ prizmada kənar uzunluğu hündürlüyə bərabərdir.
Uzunluq üçün metr və ya santimetr, sahə üçün kvadrat vahidlər, həcm üçün kub vahidlər seçilməlidir. Vahid çevirmələrini diqqətlə aparmaq vacibdir ki, nəticələr qarşılaşdırıla bilsin. Texniki sənədlərdə dəqiqlik üçün yuvarlaqlaşdırma qaydası əvvəlcədən göstərilir. Material sərfi hesablarında vahid uyğunluğu xüsusilə önəmlidir.