Riyaziyyat tarix boyu insan düşüncəsinin ən böyük nailiyyətlərindən biri sayılır. Riyazi bərabərsizliklər isə bu elmin ən fundamental bölmələrindən biridir. Onlar, yalnız məktəb və ali təhsil səviyyəsində deyil, həm də texnologiya, elm, iqtisadiyyat və gündəlik həyatda geniş tətbiq olunur. Bərabərsizliklər cəmiyyətin inkişafında, sosial və iqtisadi qərarların qəbulunda, həmçinin təbiət elmlərinin təhlilində əvəzsiz rol oynayır. Müasir riyaziyyat və tətbiqi elmlərdə bərabərsizliklərin əhəmiyyəti daim artır, çünki reallıqda bərabərliyin deyil, məhz bərabərsizliklərin hökm sürdüyü hallar daha çoxdur. Bu səbəbdən bərabərsizliklərin nəzəri və praktik əhəmiyyətini dərindən öyrənmək müasir insan üçün mühüm ehtiyacdır.
Riyazi bərabərsizliklərin anlayışı və mahiyyəti
Riyazi bərabərsizlik – bir və ya bir neçə ədədi və ya məntiqi kəmiyyətlər arasında qarşılıqlı müqayisə münasibətini ifadə edən riyazi təsirdir. Əsas məqsəd ədədlərin və ya ifadələrin hansı birinin digərindən böyük, kiçik və ya bərabər olduğunu müəyyən etməkdir. Bərabərsizliklər, adətən, “>”, “<”, “≥”, “≤” işarələri ilə göstərilir. Əslində, bərabərsizliklər real həyatda daim rast gəlinir: iqtisadi göstəricilərin müqayisəsi, sosial problemlərin təhlili, elmi proqnozlar və s. məhz bərabərsizliklərin riyazi təhlili üzərində qurulur.
Bərabərsizliklərin növləri və əsas işarələri
Riyazi bərabərsizliklər müxtəlif formalar və növlər üzrə təsnif edilir. Ən çox istifadə olunan işarələr bunlardır:
- “a > b” – a, b-dən böyükdür
- “a < b” – a, b-dən kiçikdir
- “a ≥ b” – a, b-yə bərabər və ya böyükdür
- “a ≤ b” – a, b-yə bərabər və ya kiçikdir
Bərabərsizliklər tək dəyişənli və çox dəyişənli, xətti və qeyri-xətti, riyazi və məntiqi ola bilər. Xətti bərabərsizliklər ən sadə və geniş yayılmış formadır. Qeyri-xətti bərabərsizliklər isə, məsələn, kvadrat, modul və irrasional bərabərsizliklər daha mürəkkəb struktura malik olur.
Tarixi inkişaf və nəzəri əsaslar
Bərabərsizliklərin ilk nümunələrinə qədim Babil, Misir və Yunan riyaziyyatında rast gəlinir. Böyük riyaziyyatçılar – Euklid, Arximed, İbn Sina, Al-Xarəzmi və digərləri bərabərsizliklərin müxtəlif formullarını və tətbiqlərini işləyib hazırlamışlar. 17-18-ci əsrlərdə isə bərabərsizliklərin müasir nəzəriyyəsinin təməli qoyulub. Məşhur Cauchy, Hölder, Minkowski, Chebyshev, Jensen və digər riyaziyyatçıların adları ilə bağlı bərabərsizliklər bu gün də elm aləmində geniş tətbiq olunur.
Riyazi bərabərsizliklərin əsas tip və formulları
Bərabərsizliklər arasında bir sıra universal tip və formullar xüsusi əhəmiyyət daşıyır:
Xətti bərabərsizliklər
Ən sadə forması “ax + b > 0” və ya “ax + b < 0” şəklindədir. Xətti bərabərsizliklər məktəb riyaziyyatında ən çox qarşılaşılan bərabərsizliklərdir və onların həlli üçün əsasən elementar alqoritmlər istifadə olunur.
Kvadrat və yüksək dərəcəli bərabərsizliklər
Bu tip bərabərsizliklər “ax² + bx + c > 0” və ya “ax² + bx + c < 0” kimi yazılır və həlli kök və intervalların təhlilinə əsaslanır. İrəli səviyyələrdə isə kub və daha yüksək dərəcəli bərabərsizliklər də araşdırılır.
Modul bərabərsizlikləri
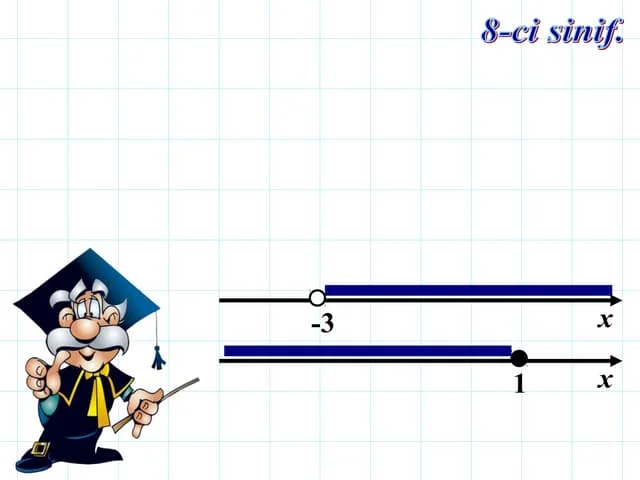
Modul bərabərsizliklər |x| < a və ya |x| > a tipində yazılır. Onların həlli x-in həm müsbət, həm də mənfi qiymətləri üçün intervallar şəklində aparılır.
Tənlik və bərabərsizlik sistemləri
Bəzən bir neçə bərabərsizlik və tənlik birlikdə sistem təşkil edir. Bu zaman onların kəsişmə və ya birgə həll sahələri araşdırılır. Xətti proqramlaşdırma, optimallaşdırma və iqtisadi modellər üçün bu tip sistemlər böyük əhəmiyyət daşıyır.
Məşhur klassik bərabərsizliklər
- Cebişev bərabərsizliyi
- Minkovski bərabərsizliyi
- Hölder bərabərsizliyi
- Kauşi-Bunyakovski bərabərsizliyi
- Jensen bərabərsizliyi
- Titu bərabərsizliyi
Bu klassik bərabərsizliklər əsasən ali riyaziyyatda, analitik, statistik və tətbiqi riyaziyyatda istifadə edilir və çox vaxt sübut, qiymətləndirmə və optimallaşdırma məsələlərində əsas alət olur.
Riyazi bərabərsizliklərin həlli üsulları
Bərabərsizliklərin həlli üçün müxtəlif üsullar mövcuddur:
- Alqoritmik metodlar – Xətti bərabərsizliklər üçün sadə ardıcıllıqla köçürmə və interval üsulu.
- Qrafik metod – Bərabərsizliklərin qrafikdə təsviri və həllinin vizual olaraq göstərilməsi.
- Təhlil və intervalların bölünməsi – Kvadrat və qeyri-xətti bərabərsizliklər üçün intervalların təhlili əsas üsuldur.
- Sistem və kompleks üsullar – Bir neçə bərabərsizlik və tənlik birlikdə sistemdə həll edilir.
Riyazi bərabərsizliklərin tətbiq sahələri
Bərabərsizliklər təkcə riyaziyyatın deyil, fizika, kimya, iqtisadiyyat, texnologiya, biologiya, informatika və hətta sosiologiya kimi sahələrin də əsas riyazi alətlərindən biridir. Məsələn:
- Fizikada enerji, impuls və digər ölçülər üçün sərhədlərin müəyyənləşdirilməsi.
- Kimyada konsentrasiyaların minimal və maksimal dəyərlərinin təyini.
- İqtisadiyyatda istehsal, xərclər və gəlirlər arasında optimal əlaqələrin qurulması.
- Biologiyada populyasiya modellərinin həddi və artım proqnozları.
- İnformatikada alqoritmlərin səmərəliliyi və yaddaş hüdudlarının təhlili.
Riyazi bərabərsizliklərin gündəlik həyatda rolu
Əslində, riyazi bərabərsizliklər gündəlik həyatımızda da daim müşahidə olunur. İstər alış-veriş zamanı büdcə planlaması, istərsə də zamanın və resursların idarə olunması, təhlükəsizlik və ehtiyat tədbirlərinin hesablanmasında bərabərsizliklər mühüm rol oynayır. Məsələn, “mənim maaşım aylıq xərclərimdən çox olmalıdır”, “sürət yolda müəyyən həddi aşmamalıdır” kimi məntiqi yanaşmalar bərabərsizliklərə əsaslanır.
Riyazi bərabərsizliklərin psixologiya və fəlsəfədə rolu
Maraqlıdır ki, bərabərsizliklər təkcə riyazi deyil, fəlsəfi və psixoloji mənada da həyatın müxtəlif sferalarında istifadə olunur. İnsanlar arasında bərabərlik və ədalət anlayışlarının, sosial bərabərsizliklərin analizi üçün də məhz riyazi bərabərsizliklərdən simvolik olaraq istifadə edilir.
Azərbaycanda riyazi bərabərsizliklərin tədrisi və tətbiqi
Azərbaycanın təhsil sistemində riyazi bərabərsizliklərin tədrisinə xüsusi əhəmiyyət verilir. Məktəb və ali məktəb proqramlarında geniş yer alan bərabərsizliklər həm şagirdlərin analitik təfəkkürünün inkişafında, həm də gələcək karyeralarında mühüm rol oynayır. Bərabərsizliklər riyaziyyat olimpiadaları, elmi layihələr və beynəlxalq müsabiqələr üçün də əsas baza hesab olunur.
Riyazi bərabərsizliklər təkcə riyaziyyatın deyil, bütövlükdə insan düşüncəsinin, elmin, texnologiyanın və gündəlik həyatın ayrılmaz hissəsidir. Onlar problemlərin həllində, qərarların qəbulunda, sosial və iqtisadi münasibətlərin tənzimlənməsində mühüm rol oynayır. Hər bir insan üçün riyazi bərabərsizlikləri öyrənmək, onları tətbiq etmək və real həyatda istifadə etmək bacarığı vacib kompetensiyadır. Gələcəyin elm və texnologiya dünyasında bərabərsizliklərin rolu daha da artacaq və yeni kəşflərin əsasını təşkil edəcək.
Ən Çox Verilən Suallar
Riyazi bərabərsizlik bir və ya bir neçə ədəd və ya ifadə arasında böyük, kiçik və ya bərabər olma münasibətini ifadə edən riyazi təsirdir.
Xətti, kvadrat, modul, irrasional, eksponensial və məntiqi bərabərsizliklər əsas növlərdir.
Xətti bərabərsizliklər elementar üsulla, kvadrat və qeyri-xətti bərabərsizliklər isə intervalların təhlili, qrafik və analitik üsullarla həll edilir.
İqtisadiyyat, fizika, kimya, biologiya, informatika və gündəlik həyatın bir çox sahəsində tətbiq edilir.
Cebişev, Minkovski, Hölder, Kauşi-Bunyakovski, Jensen, Titu və s. klassik bərabərsizliklər geniş istifadə olunur.
Modul bərabərsizliklər iki ayrı interval üzrə həll olunur: |x| < a üçün –a < x < a, |x| > a üçün isə x < –a və ya x > a.
Bəli, bərabərsizlikdə hər iki tərəfi mənfi ədədə vurduqda və ya böləndə işarə tərsinə dəyişir.
Bəli, “≥” və “≤” işarələrində bərabərlik də mümkündür.
Maliyyə, istehsal, təhlükəsizlik, texnologiya və təbiət elmlərində sərhədlərin və optimal həllərin təyinində vacib rol oynayır.
Məktəb və ali məktəb proqramlarında geniş tədris olunur, olimpiadalar və elmi layihələrdə əsas yer tutur.