Bərabəryanlı üçbucaq riyaziyyatda və geometriyada xüsusi yer tutan fiqurlardan biridir. Bu üçbucağın əsas özəlliyi iki tərəfinin bir-birinə bərabər olmasıdır ki, bu da onun daxili quruluşunda maraqlı riyazi xüsusiyyətlər yaradır. Həm məktəb proqramlarında, həm də ali riyaziyyatda bərabəryanlı üçbucaqların öyrənilməsi riyazi düşüncənin formalaşmasında mühüm rol oynayır. Üçbucaqlar arasında ən çox işlənən tiplərdən olan bərabəryanlı üçbucağın sahəsinin hesablanması, onun daxili və xarici elementləri ilə bağlı müxtəlif formul və metodlar riyaziyyatın əsas mövzularındandır. Bu fiqur həm də incəsənətdə, memarlıqda, texnikada, həndəsi modellərdə öz unikallığı ilə seçilir. Bərabəryanlı üçbucaqlar təbiətdə də tez-tez rast gəlinir və çox vaxt sabitlik, balans və simmetriya ilə əlaqələndirilir.
Bərabəryanlı üçbucağın anlayışı və əsas xüsusiyyətləri
Bərabəryanlı üçbucaq – iki tərəfi bərabər olan və bu bərabər tərəflərin qarşısındakı bucaqların da eyni dəyərə malik olduğu üçbucağa deyilir. Bu tip üçbucaqlarda bərabər tərəflərin birləşdiyi bucaq adətən əsas bucaq adlanır və digər iki bərabər olmayan tərəfinin birləşdiyi bucaq isə təpə bucağı kimi qəbul olunur. Bərabəryanlı üçbucağın bir çox maraqlı həndəsi və riyazi xüsusiyyətləri var: məsələn, bərabər tərəflərin qarşısındakı bucaqların bərabərliyi, simmetriya oxunun mövcudluğu və üçbucağın daxili hündürlüyünün bərabər tərəfə çəkildikdə həm də median, həm də bisektris və həm də ortasəth olması.
Bərabəryanlı üçbucağın quruluş elementləri
Hər bir bərabəryanlı üçbucağın üç tərəfi və üç bucağı var. Əgər üçbucağın iki tərəfi bərabərdirsə, həmin tərəflərə bərabər yanlar, digər tərəfə isə əsas tərəf deyilir. Tutaq ki, üçbucağın tərəfləri a, a və b-dirsə, burada a bərabər yanlardır, b isə əsas tərəfdir. Bərabəryanlı üçbucağın əsas xüsusiyyəti budur ki, əsas tərəfin qarşısındakı bucaq adətən ən böyük olur, bərabər tərəflərin qarşısındakı bucaqlar isə bir-birinə bərabər olur. Üçbucağın daxilində simmetriya xətti yalnız təpə bucağından əsas tərəfin ortasına endirilir və bu xətt həm hündürlük, həm median, həm də bisektris olur.
Bərabəryanlı üçbucağın sahəsinin hesablanması yolları
Bərabəryanlı üçbucağın sahəsi müxtəlif üsullarla hesablanır və bu, üçbucağın hansı elementlərinin (tərəf, hündürlük, bucaq və s.) verilməsindən asılıdır. Ən geniş yayılmış və istifadə olunan formullardan bəziləri bunlardır:
1. Əsas tərəf və hündürlük vasitəsilə sahə
Əgər əsas tərəfin uzunluğu b və ona çəkilən hündürlük h-dirsə, sahə aşağıdakı kimi hesablanır:
S = (b × h) / 2
2. Bərabər yan və əsas tərəflər vasitəsilə sahə
Bərabəryanlı üçbucağın bərabər yan tərəfləri a, əsas tərəfi b-dirsə, hündürlük pifaqor teoreminə əsasən belə tapılır:
h = √[a² – (b²/4)]
Sonra isə sahə:
S = (b × h) / 2
3. Yan tərəf və təpə bucağı vasitəsilə sahə
Əgər yan tərəfin uzunluğu a, təpə bucağı isə α-dırsa, sahə trigonometriyanın köməyi ilə belə tapılır:
S = (a² × sin(α)) / 2
4. Heron düsturu ilə sahə
Heron düsturu da bərabəryanlı üçbucaqlar üçün istifadə olunur. Tərəfləri a, a, b olan üçbucaq üçün yarımpərimetr belədir:
p = (a + a + b) / 2 = (2a + b) / 2
Sahə isə:
S = √[p × (p – a) × (p – a) × (p – b)]
5. Bucaqlar vasitəsilə sahə
Bərabəryanlı üçbucağın bütün bucaqları bilindiyi halda, tərəf uzunluqları trigonometriya ilə tapılıb sahə hesablana bilər.
Sahənin tapılması üçün əyani nümunələr
Bərabəryanlı üçbucağın sahəsinin hesablanmasında müxtəlif real həyatdan və riyazi məsələlərdən nümunələr təqdim etmək mümkündür. Məsələn, əsas tərəfi 10 sm, bərabər yan tərəfi 13 sm olan bərabəryanlı üçbucağın sahəsini tapaq:
Hündürlük:
h = √[13² – (10² / 4)] = √[169 – 25] = √144 = 12 sm
Sahə:
S = (10 × 12) / 2 = 60 sm²
Başqa bir nümunədə isə təpə bucağı 40°, bərabər yan tərəfi 7 sm olan üçbucağın sahəsini tapmaq üçün:
S = (7² × sin(40°)) / 2 ≈ (49 × 0.6428) / 2 ≈ 15.73 sm²
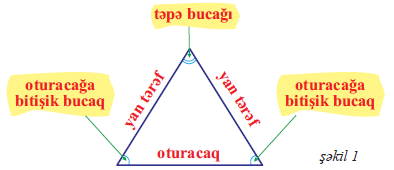
Bərabəryanlı üçbucağın əsas həndəsi və riyazi xüsusiyyətləri
Bərabəryanlı üçbucaqların həndəsi xüsusiyyətləri çoxşaxəlidir. Onların daxilindəki hündürlüklərin, medianların, bisektris və ortasəthin bir-birinə bərabər olması simmetriya baxımından maraqlı nəticələrə səbəb olur. Bərabəryanlı üçbucağın daxilində çəkilmiş hündürlük, median, bisektris və ortasəth bərabər yanlara çəkildikdə eyni xətt olur. Həmçinin, bu tip üçbucaqlarda əsas tərəfə çəkilmiş hündürlük həmişə ən qısa məsafədir.
Bərabəryanlı üçbucaqların təbiətdə və incəsənətdə rolu
Bərabəryanlı üçbucaqlar təbiətdə, memarlıqda, incəsənətdə və texnikada geniş tətbiq olunur. Dağların, bitkilərin, heyvanların bədənində, eləcə də arxitektur qurğularda tez-tez bərabəryanlı üçbucaqlara rast gəlinir. Onlar simmetriyanın, harmoniyanın, sabitliyin və estetikanın rəmzi kimi çıxış edir. Çadır, köşk, dam örtükləri və bir çox tikililərdə bərabəryanlı üçbucağın forması xüsusi mühəndislik və memarlıq əhəmiyyətinə malikdir.
Bərabəryanlı üçbucağın sahəsinin tətbiqi sahələri
Üçbucağın sahəsinin hesablanması müxtəlif real həyati və elmi sahələrdə istifadə edilir. Məsələn, torpaq ölçmələrində, memarlıq layihələrində, incəsənət kompozisiyalarında, riyazi modelləşdirmələrdə və proqramlaşdırmada bərabəryanlı üçbucaqların sahəsi tez-tez istifadə olunur. Sahənin dəqiq hesablanması, planlaşdırma və optimal qərarların qəbulunda əvəzsizdir.
Riyaziyyat dərslərində bərabəryanlı üçbucağın öyrədilməsi
Azərbaycan məktəblərində və ali təhsil müəssisələrində bərabəryanlı üçbucağın mövzusu əsasən 6-7-ci siniflərdə başlanır və sonrakı mərhələlərdə dərinləşdirilir. Riyaziyyat müəllimləri şagirdlərə sahənin müxtəlif üsullarla hesablanmasını, həndəsi və riyazi xüsusiyyətlərini praktiki və nəzəri cəhətdən izah edirlər. Olimpiadalarda, fənn müsabiqələrində və müxtəlif riyazi yarışlarda bərabəryanlı üçbucaqların sahəsi tez-tez qarşıya çıxan məsələlərdəndir.
Bərabəryanlı üçbucağın sahəsi ilə bağlı tez-tez edilən səhvlər
Bu mövzuda əsas problemlərdən biri formulun düzgün seçilməməsi, hündürlüyün yanlış hesablanması və ya verilənlərin düzgün yerləşdirilməməsidir. Şagirdlər tez-tez əsas tərəf və yan tərəfləri qarışdırır, hündürlüyü tapanda yanlış üsuldan istifadə edir və nəticədə səhv cavablar alırlar. Həmçinin, bəzi məsələlərdə bucaqların dərəcələrlə deyil, radianlarla verilməsi əlavə çaşqınlığa səbəb ola bilər.
Bərabəryanlı üçbucağın sahəsi riyaziyyat və həndəsənin fundamental məsələlərindən biri olub, həm nəzəri, həm də praktiki baxımdan xüsusi əhəmiyyətə malikdir. Sahənin hesablanmasının bir neçə fərqli üsulu var və hər biri müxtəlif situasiyalarda tətbiq edilir. Bərabəryanlı üçbucağın öyrənilməsi şagird və tələbələrin məntiqi düşüncəsinin, həndəsi təfəkkürünün inkişafına, riyazi məsələlərin həllində çevik və yaradıcı yanaşma bacarığının formalaşmasına səbəb olur. Üçbucaqların bu növü, eləcə də onların sahəsinin dəqiq hesablanması riyaziyyatda, texnikada və gündəlik həyatda qarşıya çıxan bir çox məsələlərin uğurla həllinə imkan verir.
Ən Çox Verilən Suallar
Bərabəryanlı üçbucaq iki tərəfi bərabər olan və bərabər tərəflərin qarşısındakı bucaqları eyni olan üçbucağa deyilir.
Əsas tərəf və hündürlük verilibsə S=(b×h)/2, yan tərəf və təpə bucağı verilibsə S=(a²×sin(α))/2, həmçinin Heron düsturundan da istifadə oluna bilər.
Tərəflər a, a, b-dirsə, yarımpərimetr p=(2a+b)/2, sahə isə S=√[p×(p-a)×(p-a)×(p-b)] formuluna görə tapılır.
Əsas tərəf və ona çəkilmiş hündürlük, iki yan tərəf və aralarındakı bucaq, yaxud bütün tərəflərin uzunluqları məlum olmalıdır.
Yan tərəf a, əsas tərəf b-dirsə, h=√[a²-(b²/4)] düsturuna görə tapılır.
Bərabər yanların ortasından əsas tərəfin ortasına çəkilən xətt həm hündürlük, həm median, həm bisektris, həm də ortasəth olur.
Torpaq ölçmələrində, memarlıqda, incəsənət kompozisiyalarında, riyazi modellərdə və proqramlaşdırmada istifadə olunur.
Onlar simmetriya, harmoniya, sabitlik və estetik tarazlığın rəmzidir.
Bərabəryanlı üçbucaq və onun sahəsi əsasən riyaziyyatın 6-7-ci sinif dərslərində və ali məktəb proqramlarında tədris olunur.
Əsas tərəf və yan tərəfi səhv salmaq, hündürlüyü yanlış hesablamaq, formul seçmədə səhv etmək və bucağın dərəcə-radian çevrilməsinə diqqət yetirməmək.