Bölünmə əlamətləri riyaziyyatın ən vacib mövzularından biri kimi məktəb illərindən hər kəs üçün tanışdır. Bu anlayışlar, sadə və mürəkkəb ədədlərin bölünməsini, onların hansı ədədə tam bölündüyünü müəyyənləşdirməyə imkan verir. Hesablamalarda vaxtı qısaltmaq, sürətli qərar vermək və məntiqi inkişaf etdirmək üçün bölünmə əlamətlərinin bilik səviyyəsi mühüm rol oynayır. Riyazi tapşırıqlar, testlər və gündəlik həyatdakı sadə bölmələrdə ədədlərin hansı hallarda tam bölündüyünü bilməklə, məntiqi və analitik düşüncə daha da güclənir. Hər bir ədədin bölünmə əlamətlərini mənimsəmək həm məktəblilər, həm də böyüklər üçün praktiki əhəmiyyət daşıyır.
Bölünmə əlamətləri, əsasən, 2, 3, 4, 5, 6, 8, 9, 10 və 100 kimi əsas ədədlər üçün daha tez-tez istifadə edilir. Müasir dövrdə bu qaydalar təkcə məktəb proqramı üçün deyil, gündəlik həyat, iqtisadiyyat və elm sahələrində də istifadə olunur. Riyaziyyat dərslərində bölünmə əlamətlərinin izahı və praktik tətbiqi uşaqların marağını artırır, məntiqi düşüncəni formalaşdırır və riyazi tapşırıqları daha asan həll etməyə kömək edir. İbtidai siniflərdə başlayan bu mövzu, ali riyaziyyatda da öz aktuallığını qoruyur.
Bölünmə Əlamətinin Əsas Mahiyyəti
Bölünmə əlaməti – verilmiş ədədin müəyyən bir ədədə tam bölünüb-bölünmədiyini yoxlamağa imkan verən qaydalardır. Bu qaydalar sürətli hesablama üçün çox əlverişlidir və tez qərar verməyə imkan yaradır.
Əlamətlər əsasən ən çox istifadə olunan ədədlər üçün öyrədilir. Onların köməyi ilə böyük ədədləri hissələrə ayırmaq və analiz etmək mümkündür.
2-Yə Bölünmə Əlaməti
Hər hansı bir ədədin son rəqəmi cütdürsə (0, 2, 4, 6, 8), o ədəd 2-yə tam bölünür. Bu, bölünmə əlamətləri içərisində ən sadə və tez xatırlananıdır.
Məsələn, 354, 1026, 88 kimi ədədlərin son rəqəmi cütdür, ona görə də bu ədədlər 2-yə bölünür.
3-ə Bölünmə Əlaməti
Bir ədədin bütün rəqəmlərinin cəmi 3-ə bölünürsə, həmin ədəd də 3-ə tam bölünür. Məsələn, 213 (2+1+3=6), 6 ədədi 3-ə bölündüyü üçün 213 də 3-ə tam bölünür.
Bu qayda böyük ədədlər üçün də keçərlidir və sadə hesablama imkanı yaradır.
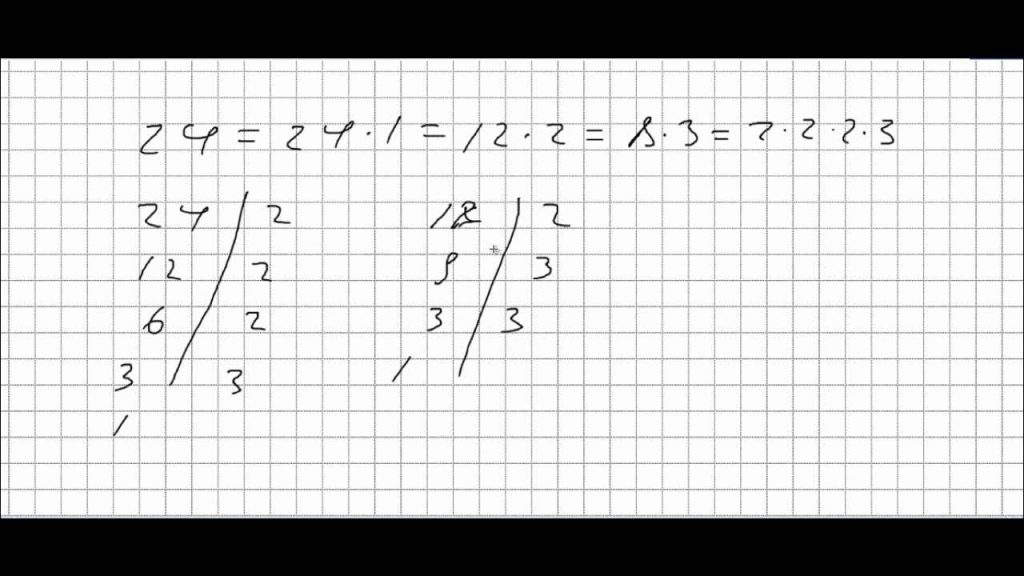
5-ə və 10-a Bölünmə Əlamətləri
Bir ədədin sonu 0 və ya 5 ilə bitirsə, həmin ədəd 5-ə tam bölünür. Əgər yalnız 0 ilə bitirsə, o zaman həm də 10-a tam bölünür.
Məsələn, 245 (sonu 5-dir), 140 (sonu 0-dır) – bu ədədlər asanlıqla 5-ə və ya 10-a bölünür.
4-ə Bölünmə Əlaməti
Hər hansı bir ədədin son iki rəqəmi 4-ə bölünürsə, həmin ədəd 4-ə tam bölünür. Bu, əsasən dörd rəqəmli və daha böyük ədədlər üçün praktikdir.
Məsələn, 1312 (12 son iki rəqəm 4-ə bölünür), 2516 (16 4-ə bölünür).
9-a Bölünmə Əlaməti
Ədədin bütün rəqəmlərinin cəmi 9-a bölünürsə, həmin ədəd 9-a da tam bölünür. Bu qayda 3-ə bölünmə əlamətinə bənzəyir, ancaq burada 9-a bölünmə yoxlanılır.
Məsələn, 729 (7+2+9=18; 18 də 9-a bölünür), 954 (9+5+4=18).
6-ya və 12-yə Bölünmə Əlamətləri
Bir ədəd həm 2-yə, həm də 3-ə bölünürsə, o ədəd 6-ya da tam bölünür. 12-yə bölünmə üçün isə ədəd həm 3-ə, həm də 4-ə tam bölünməlidir.
Bu əlamət daha mürəkkəb bölünmə üçün istifadə edilir və yoxlama prosesi iki addımdan ibarətdir.
8-ə Bölünmə Əlaməti
Bir ədədin son üç rəqəmi 8-ə bölünürsə, həmin ədəd 8-ə tam bölünür. Bu qayda çoxrəqəmli ədədlər üçün əlverişlidir.
Məsələn, 3016 (son üç rəqəm 016, 16 isə 8-ə bölünür).
100-ə Bölünmə Əlaməti
Bir ədədin son iki rəqəmi sıfırdırsa, həmin ədəd 100-ə tam bölünür. 1000-ə bölünmə üçün isə son üç rəqəm sıfır olmalıdır.
Bu, xüsusilə böyük ədədlər üçün istifadə edilən sadə qaydadır.
Cədvəl: Əsas Bölünmə Əlamətləri
| Ədəd | Bölünmə Əlaməti | Misal |
|---|---|---|
| 2 | Son rəqəm cütdür | 234, 128 |
| 3 | Rəqəmlərin cəmi 3-ə bölünür | 123, 321 |
| 4 | Son iki rəqəm 4-ə bölünür | 1112, 3216 |
| 5 | Son rəqəm 0 və ya 5-dir | 125, 230 |
| 6 | 2-yə və 3-ə bölünür | 132, 258 |
| 8 | Son üç rəqəm 8-ə bölünür | 1016, 2008 |
| 9 | Rəqəmlərin cəmi 9-a bölünür | 234, 729 |
| 10 | Son rəqəm sıfırdır | 130, 340 |
| 100 | Son iki rəqəm sıfırdır | 1200, 4500 |
Bölünmə əlamətləri, həm məktəb yaşlı uşaqlar, həm də böyüklər üçün riyazi əməliyyatların sürətli və asan şəkildə yerinə yetirilməsində mühüm vasitədir. Bu qaydaların bilik səviyyəsi analitik düşüncənin inkişafı və gündəlik riyazi məsələlərin effektiv həllində əvəzolunmaz rol oynayır. Həm təhsil, həm də peşə fəaliyyətində bu əlamətləri praktikada tez-tez tətbiq etmək mümkündür. Analitik düşüncəni, məntiqi və riyazi təfəkkürü artırmaq üçün bölünmə əlamətlərinin hər yaşda mənimsənilməsi vacibdir. Müasir tədris proqramlarında və gündəlik riyaziyyatda bölünmə əlamətləri mövzusu öyrənmək və tətbiq etmək üçün mütləq lazımlı hesab edilir.
Ən Çox Verilən Suallar
Bölünmə əlaməti müəyyən bir ədədin seçilmiş digər ədədə tam bölünüb-bölünmədiyini yoxlamağa imkan verən sadə riyazi qaydalardır. Bu qaydalar vasitəsilə bölmə əməliyyatı asanlaşır.
Ədədin son rəqəmi cütdürsə (0, 2, 4, 6, 8), həmin ədəd 2-yə tam bölünür. Bu, ən asan və tez yoxlanan bölünmə əlamətidir.
Bir ədədin bütün rəqəmlərinin cəmini hesablamaq lazımdır. Əgər cəm 3-ə bölünürsə, əsas ədəd də 3-ə tam bölünür.
Ədədin sonu 0 və ya 5-lə bitirsə, 5-ə tam bölünür. Yalnız 0-lə bitirsə, həm də 10-a tam bölünür.
Ədədin son iki rəqəmi 4-ə bölünürsə, həmin ədəd 4-ə tam bölünür. Bu, əsasən dördrəqəmli və daha böyük ədədlər üçün uyğundur.
Ədədin bütün rəqəmlərinin cəmi 9-a bölünürsə, həmin ədəd də 9-a tam bölünür. Bu qayda böyük ədədlər üçün də keçərlidir.
Bir ədəd həm 2-yə, həm də 3-ə bölünürsə, o ədəd 6-ya tam bölünür. Bu qayda iki şərti eyni vaxtda yoxlamaqla müəyyən edilir.
Ədədin son üç rəqəmi 8-ə bölünürsə, həmin ədəd 8-ə tam bölünür. Xüsusilə çoxrəqəmli ədədlər üçün istifadə olunur.
Bir ədədin son iki rəqəmi sıfırdırsa, həmin ədəd 100-ə, son üç rəqəmi sıfırdırsa 1000-ə tam bölünür.
Bölünmə əlamətləri riyaziyyat tapşırıqlarının asan və tez həllində, gündəlik hesablamalarda, analitik düşüncənin inkişafında və riyazi problemlərin sürətli cavablandırılmasında vacib rol oynayır.