Riyaziyyat elminin ən mühüm bölmələrindən biri olan həndəsə, müstəvi üzərində müxtəlif fiqurların öyrənilməsini əhatə edir. Bu fiqurlardan biri də çevrədir. Çevrə dedikdə, mərkəzdən bərabər məsafədə olan nöqtələrin birləşməsindən yaranan qapalı əyri nəzərdə tutulur. Çevrə yalnız sadə həndəsi fiqur deyil, həm də analitik həndəsədə geniş istifadə olunan riyazi modeldir. Riyazi baxımdan çevrənin tənliyi bu fiqurun analitik təmsilidir.
Çevrənin tənliyi, yəni onun koordinat müstəvisində ifadəsi, riyaziyyatın çoxsaylı sahələrində mühüm rol oynayır. Bu tənlik vasitəsilə çevrəni analitik şəkildə təsvir etmək, onun radiusunu, mərkəzini və digər xüsusiyyətlərini asanlıqla tapmaq mümkündür. Həmçinin, bu tənliklər riyazi modelləşdirmədə, qrafik analizlərdə, fiziki sistemlərin riyazi təhlilində və kompüter qrafikasında geniş tətbiq olunur.
Məktəblərdə və ali məktəblərdə analitik həndəsə bölməsində tədris edilən bu mövzu həm məntiqi düşüncəni inkişaf etdirir, həm də koordinat sistemində fiqurların davranışını başa düşməkdə mühüm rol oynayır. Çevrənin tənliyi ilə tanış olan şagird və tələbələr sonrakı riyazi anlayışlara daha tez yiyələnə bilirlər. Eləcə də bu bilik mühəndislik, memarlıq, proqramlaşdırma və robot texnikası kimi sahələrdə real tətbiq sahəsinə malikdir.
Çevrə nədir və riyazi anlayışı
Çevrə, müstəvidə müəyyən bir nöqtədən bərabər məsafədə yerləşən nöqtələrin cəmi ilə alınan qapalı əyridir. Bu nöqtə çevrənin mərkəzi adlanır, həmin bərabər məsafə isə radius kimi tanınır. Çevrə simmetrik və sabit məsafəli struktur olduğuna görə həm həndəsi, həm də riyazi baxımdan asanlıqla modelləşdirilə bilir.
Əgər çevrənin mərkəzi M(a,b)M(a,b) nöqtəsində yerləşirsə və radiusu rr olarsa, çevrədəki istənilən P(x,y)P(x,y) nöqtəsi ilə mərkəz arasındakı məsafə radiusa bərabərdir. Bu məsafəni tapmaq üçün məsafə formulundan istifadə olunur. Bu, tənliyin əsasını təşkil edir.
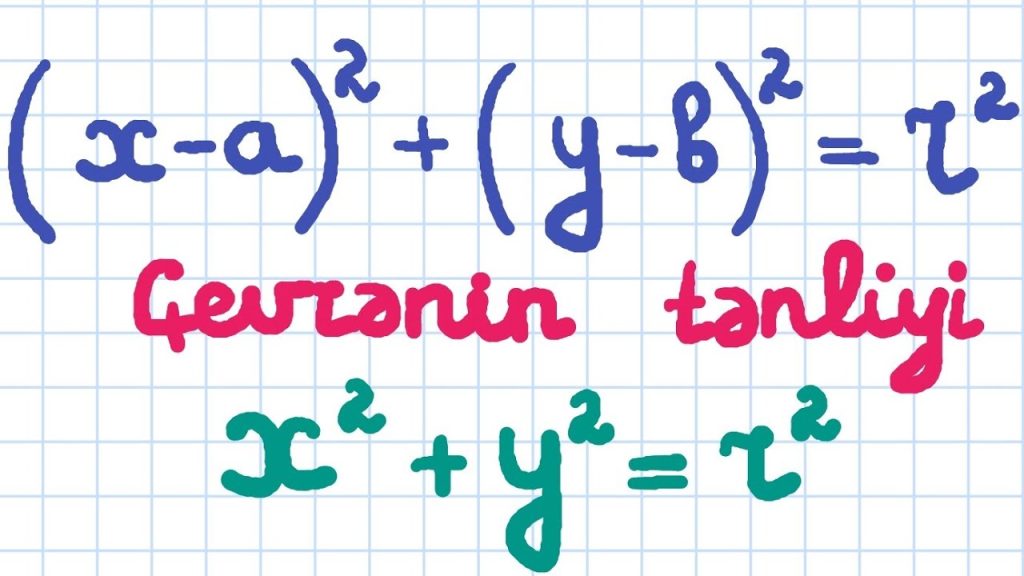
Çevrənin ümumi tənliyi
Çevrənin mərkəz-radius formasında tənliyi belədir:(x−a)2+(y−b)2=r2(x−a)2+(y−b)2=r2
Burada:
- (a,b)(a,b) — çevrənin mərkəzidir.
- rr — radiusdur.
- (x,y)(x,y) — çevrə üzərində yerləşən istənilən nöqtədir.
Bu tənlik çevrənin bütün nöqtələrinin mərkəzdən eyni məsafədə olduğunu göstərir. Əgər mərkəz (0,0)(0,0) nöqtəsində yerləşirsə, yəni çevrə koordinat başlanğıcında yerləşirsə, tənlik sadələşir:x2+y2=r2x2+y2=r2
Bu forma çevrənin ən sadə və ən çox istifadə olunan tənliyidir.
Tənliyin həndəsi mənası
Çevrənin tənliyi əslində radius sabit olmaqla mərkəz nöqtədən müəyyən məsafədə yerləşən nöqtələrin cəmini ifadə edir. Tənlikdəki kvadrat ifadələr — (x−a)2(x−a)2 və (y−b)2(y−b)2 — nöqtənin mərkəzdən məsafəsinin kvadratını göstərir. Tənliyin sağ tərəfində isə bu məsafənin — radiusun — kvadratı dayanır.
Bu, o deməkdir ki, tənlikdə istənilən xx və yy cütü yalnız həmin məsafəyə (radiusa) uyğun olduqda tənliyi ödəyir. Əgər bir nöqtənin koordinatları bu tənliyi ödəyirsə, deməli o nöqtə çevrə üzərində yerləşir. Bu, həm təhlil, həm də qrafik quruluş zamanı çevrəni müəyyən etməyə imkan verir.
Tənliyin ümumi forması və çevrilməsi
Çevrənin tənliyinin başqa bir ümumi forması da mövcuddur:x2+y2+Dx+Ey+F=0x2+y2+Dx+Ey+F=0
Bu tənlikdə DD, EE, və FF — real ədədlərdir və tənlik kvadrat şəkildə ifadə olunur. Bu formadakı tənlikdə mərkəz və radius birbaşa görünmür, lakin uyğun çevrilmələrlə (tam kvadratlara gətirmə) onları tapmaq mümkündür.
Tənliyi kvadrat formasından mərkəz-radius formasına çevirmək üçün tam kvadratlara gətirmə üsulundan istifadə olunur. Bu üsulla mərkəz nöqtəsinin koordinatlarını və radiusun ölçüsünü hesablamaq mümkündür. Bu çevrilmə həm alqoritmik təhlil, həm də qrafik təsvir üçün olduqca faydalıdır.
Praktiki misallar və tənlik quruluşu
Nümunə 1: Mərkəzi (2,−3)(2,−3), radiusu 55 olan çevrənin tənliyini qurun.
Tətbiq edək:(x−2)2+(y+3)2=25(x−2)2+(y+3)2=25
Nümunə 2: Aşağıdakı tənliyi mərkəz-radius formasına gətirin:x2+y2−4x+6y−3=0x2+y2−4x+6y−3=0
Tam kvadratlara gətirək:(x2−4x)+(y2+6y)=3(x2−4x)+(y2+6y)=3(x−2)2−4+(y+3)2−9=3(x−2)2−4+(y+3)2−9=3(x−2)2+(y+3)2=16(x−2)2+(y+3)2=16
Deməli, mərkəz (2,−3)(2,−3), radius 44.
Bu cür praktiki misallar tənliyin tətbiqini daha da aydınlaşdırır.
Qrafik və vizual təhlil
Çevrənin tənliyi qrafikdə dairəvi forma ilə təmsil olunur. Bu qrafik quruluş çevrənin mərkəzinin və radiusunun vizual olaraq necə dəyişdiyini göstərməyə imkan verir. Əgər mərkəz dəyişirsə, çevrə koordinat müstəvisində yerini dəyişir, radius dəyişirsə, çevrənin böyüklüyü dəyişir.
Riyaziyyat dərslərində bu qrafiklərlə işləmək, çevrənin tənliyinə verilən nöqtələrin çevrə üzərində olub-olmadığını yoxlamaq, iki çevrənin bir-birinə görə mövqeyini təyin etmək və digər analizlər üçün vacibdir. Qrafik təsvir tənliyin yalnız riyazi deyil, həm də vizual mənimsənilməsinə kömək edir.
Çevrə tənliyinin tətbiq sahələri
Çevrə tənliyi məktəbdə sadə tədris materialı olmaqla yanaşı, real həyatda da çoxsaylı sahələrdə tətbiq olunur. Kompüter qrafikasında çevrə modellərinin qurulması, robotların trayektoriyasının hesablanması, optik sistemlərin modelləşdirilməsi, GPS sistemlərinin trayektoriya hesablamaları bu tənliyin tətbiqinə əsaslanır.
Mühəndislikdə əyri səthlərin analizi, aerokosmik texnologiyada peyklərin trayektoriyası, hətta animasiya və oyun dizaynında obyektlərin hərəkət istiqaməti çevrə tənliyinə uyğun qurulur. Bu tənlik riyaziyyatın praktik gücünü göstərən konkret nümunələrdən biridir.
Müxtəlif parametrlərə görə çevrənin tənliyi
| Mərkəz nöqtəsi (a, b) | Radius (r) | Tənlik |
|---|---|---|
| (0, 0) | 5 | x² + y² = 25 |
| (3, -2) | 4 | (x – 3)² + (y + 2)² = 16 |
| (-1, 1) | √2 | (x + 1)² + (y – 1)² = 2 |
| (2, 2) | 6 | (x – 2)² + (y – 2)² = 36 |
Bu cədvəl çevrə tənliyinin necə qurulduğunu və mərkəzlə radiusun tənlikdə necə əks olunduğunu sistemləşdirilmiş şəkildə göstərir.
Çevrənin tənliyi riyaziyyatda həm nəzəri, həm də praktik əhəmiyyətə malik mühüm anlayışlardan biridir. Onun vasitəsilə koordinat müstəvisində dairəvi fiqurların analitik təsviri aparılır, qrafik qurulur və mühəndislikdən texnologiyaya qədər müxtəlif sahələrdə tətbiq edilir. Bu tənlik radius və mərkəzə əsaslanır və həm sadə, həm də ümumi formaları ilə istifadə oluna bilər.
Tənlik vasitəsilə çevrənin geometrik quruluşunu analiz etmək, müxtəlif vəziyyətlərdə dəyişməsini təhlil etmək mümkündür. Çevrənin tənliyini düzgün qurmaq və başa düşmək, daha mürəkkəb həndəsi fiqurların və sistemlərin modelləşdirilməsinə zəmin yaradır.
Analitik həndəsə riyaziyyatın tətbiqi sahələrinə giriş üçün möhkəm bünövrədir və çevrə tənliyi bu bünövrənin əsas sütunlarındandır. Riyazi savadlılıq, məntiqi düşüncə və texniki təfəkkür bu anlayışla inkişaf edir və şagirdlərin elmi potensialının formalaşmasına kömək edir.
Ən Çox Verilən Suallar
Çevrənin tənliyi, koordinat müstəvisində yerləşən çevrənin analitik təsviridir. Bu tənlik çevrənin mərkəzi və radiusu əsasında qurulur. Ən çox istifadə olunan forma (x – a)² + (y – b)² = r² şəklindədir. Burada (a, b) mərkəz, r isə radiusdur.
Çevrənin tənliyi mərkəz-radius formasında belə yazılır: (x – a)² + (y – b)² = r². Burada (a, b) çevrənin mərkəzinin koordinatlarıdır, r isə radiusdur. Əgər mərkəz (0,0)-da yerləşirsə, tənlik x² + y² = r² şəklini alır.
Ümumi çevrə tənliyi kvadrat şəkildə belə yazılır: x² + y² + Dx + Ey + F = 0. Bu formadan tam kvadratlara gətirmə üsulu ilə mərkəz və radius tapıla bilər. Bu forma qrafik və alqoritmik təhlillərdə tez-tez istifadə olunur.
Əgər çevrə ümumi formada verilibsə, məsələn, x² + y² + Dx + Ey + F = 0, bu tənlik tam kvadratlara gətirilərək mərkəz (a, b) və radius r tapılır. Bu zaman kvadrat tamamlanması üsulu tətbiq olunur.
Çevrə tənliyi memarlıqda, mühəndislikdə, kompüter qrafikasında, peyk sistemlərində və GPS texnologiyalarında istifadə olunur. Bu tənliklə obyektlərin dairəvi trayektoriyaları analiz edilir və modelləşdirilir.
Çevrə tənliyinin qrafiki koordinat müstəvisində mərkəzi (a, b) olan və radiusu r olan dairəvi əyridir. Bu qrafik çevrənin hansı nöqtələrdən keçdiyini və koordinat sistemində yerləşməsini göstərir.
Radius dəyişdikdə, tənliyin sağ tərəfindəki r² dəyəri dəyişir. Bu da çevrənin sahəsinin və ölçüsünün böyüməsinə və ya kiçilməsinə səbəb olur. Mərkəz dəyişməz qaldıqda yalnız çevrənin ölçüsü dəyişir.
Əgər çevrənin mərkəzi dəyişərsə, tənlikdə (x – a) və (y – b) ifadələrindəki a və b dəyərləri dəyişir. Bu da çevrənin koordinat müstəvisində yeni bir yerə daşınmasına səbəb olur.
Əgər çevrə ümumi formada verilibsə, tənliyi sadələşdirmək üçün kvadrat tamamlanması üsulu ilə mərkəz-radius formasına gətirilir. Bu üsul həm radiusun, həm də mərkəzin tapılmasını asanlaşdırır.
Çevrənin tənliyi Azərbaycan məktəblərində əsasən 8-ci və ya 9-cu siniflərdə analitik həndəsə bölməsində tədris olunur. Bu mövzu riyazi modelləşdirmə və qrafik analizlərin əsasını təşkil edir.