Hər bir təbiət hadisəsi və fiziki anlayış kimi, çevrə də insan həyatında həm nəzəri, həm də praktik baxımdan mühüm rol oynayır. Riyaziyyatın ən əsas mövzularından biri olan çevrə, yalnız təhsil mühitində deyil, gündəlik həyatda da geniş tətbiq sahəsinə malikdir. İnsan minilliklər boyu formaların mükəmməlliyini anlamağa çalışmış və ən sadə, eyni zamanda ən mürəkkəb formalardan biri olan dairəni və onun sərhədi olan çevrəni öyrənmişdir. Bu anlayış həm geometriyada, həm də fizikanın müxtəlif sahələrində öz aktuallığını qoruyub saxlamışdır.
Çevrə yalnız mücərrəd riyazi obyekt deyil, real həyatda bizi əhatə edən əşyaların, təbiət hadisələrinin və mühəndislik həllərinin ayrılmaz hissəsidir. Təkərin forması, saatların üzü, planetlərin orbitləri, musiqi alətlərinin rezonans dairələri – bütün bunlar çevrənin müxtəlif təzahürləridir. Bu baxımdan çevrə anlayışını dərk etmək, sadəcə nəzəri bilik əldə etmək deyil, həm də ətraf aləmi daha dərindən anlamaq deməkdir.
Geometriyada çevrə radius, diametr və mərkəz anlayışları ilə sıx bağlıdır. Bu elementlər yalnız riyazi düsturların qurulmasında deyil, praktiki ölçmələrdə də böyük əhəmiyyət kəsb edir. Çevrənin uzunluğunu hesablamaq üçün π (pi) sabitinin tətbiqi isə insan ağlının simmetriya və harmoniya axtarışının təcəssümüdür. Bu sabit qədim dövrlərdən günümüzədək elm və texnologiyada öz mövqeyini qorumaqdadır.
Çevrənin məna və mahiyyətini anlamaq üçün yalnız onun riyazi tərifinə baxmaq kifayət deyil. Həmçinin onun təbiətdə, sənətdə, memarlıqda və gündəlik həyatda necə tətbiq olunduğunu da izləmək lazımdır. Əslində, insanın estetik duyğularında da çevrə simmetriyanın və mükəmməlliyin rəmzi kimi dərin iz buraxmışdır. Hər bir dairənin sərhədi olan çevrə, bəşəriyyətin sonsuzluğa və ahəngə olan marağını əks etdirir.
Çevrənin tərifi və əsas anlayışlar
Çevrə, mərkəzdən eyni məsafədə yerləşən bütün nöqtələrin birləşməsidir. Bu məsafə radius adlanır və çevrənin əsas elementlərindən biridir. Əgər radius iki dəfə götürülərsə, diametr meydana gəlir ki, bu da çevrənin ən uzun düz xətt seqmentidir. Çevrənin uzunluğu isə radius və π sabitindən asılı olaraq hesablanır. Riyaziyyatın bu sadə qaydası həm təhsil mühitində, həm də praktik ölçmələrdə geniş istifadə edilir.
Mərkəz, radius və diametr kimi anlayışlar çevrəni anlamaq üçün əsas baza rolunu oynayır. Çevrənin daxilində yerləşən bütün nöqtələr mərkəzə radiusdan az məsafədədir, kənarında yerləşənlər isə radiusdan çox məsafədə. Bu cür dəqiq təriflər riyazi obyektlərin sərhədlərini anlamaqda kömək edir. Həmçinin çevrə üzərindəki qövs, bucaqlar və kəsiklər də onun riyazi dəyərlərini zənginləşdirir.
Çevrənin uzunluğu və sahəsi
Çevrənin uzunluğu C = 2πr düsturu ilə hesablanır. Burada r radius, π isə sabit ədəddir. Bu düstur həm nəzəri, həm də praktik məsələlərin həllində geniş istifadə olunur. Məsələn, mühəndislikdə dairəvi konstruksiyaların perimetrlərinin ölçülməsi zamanı bu düsturdan istifadə edilir. Təbiətdə isə planetlərin orbitlərinin uzunluqlarını hesablamaq üçün tətbiq olunur.
Çevrə ilə sıx bağlı olan dairənin sahəsi isə S = πr² düsturu ilə tapılır. Bu düstur riyaziyyat dərslərinin ən məşhur formulalarından biridir. Həmçinin gündəlik həyatda dairəvi masaların, boşqabların və digər əşyaların sahəsini ölçmək üçün də bu düstur tətbiq oluna bilər. Bu sadə, lakin fundamental düsturlar insanın həm məntiqi düşüncəsini, həm də praktik bacarığını inkişaf etdirir.
Çevrə və incəsənət
İncəsənətdə çevrə mükəmməlliyin və ahəngin simvolu hesab edilir. İslam memarlığında dairəvi qübbələr və ornamentlər geniş şəkildə istifadə olunmuşdur. Qərb incəsənətində də çevrəvi formalar kilsə pəncərələrində, rəsmlərdə və heykəltəraşlıq əsərlərində rast gəlinir. Hətta Leonardo da Vinçinin məşhur “Vitruvian adam” əsərində insan bədəninin proporsiyaları çevrə ilə əlaqələndirilmişdir.
Musiqidə də çevrənin simvolizmi öz əksini tapıb. Səs dalğalarının harmoniyası və musiqi alətlərinin rezonans xassələri çevrə ilə sıx bağlıdır. Bu da göstərir ki, insan yaradıcılığında çevrə yalnız riyazi yox, həm də estetik məna daşıyır.
Çevrə və texnologiya
Müasir texnologiyada çevrənin tətbiqi olduqca genişdir. Avtomobillərin təkərləri, mexaniki dişlilər, saat mexanizmləri – hamısı çevrə formasına əsaslanır. Elektronika və kompüter texnologiyalarında da dairəvi formaların istifadəsi mühüm əhəmiyyət kəsb edir. Məsələn, disklər və CD-lər məlumat saxlama üçün çevrəvi struktura malikdir.
Optik cihazlarda linzaların dairəvi forması işığın düzgün istiqamətləndirilməsini təmin edir. Həmçinin aerodinamika və hidrodinamika sahələrində də dairəvi formalar mühüm rol oynayır. Bu tətbiqlər bir daha göstərir ki, çevrə yalnız nəzəri riyaziyyat deyil, həm də texnologiyanın təməl elementlərindən biridir.
Çevrənin gündəlik həyatda istifadəsi
Gündəlik həyatda çevrəyə hər addımda rast gəlinir. Masaların, boşqabların, saatların forması dairəvidir. Uşaqların sevimli oyuncaqlarında da çevrə motivləri mövcuddur. Bu formalar həm praktiklik, həm də estetik cəhətdən rahatlıq təmin edir. İnsan zehni də simmetrik formaları daha tez qəbul edir ki, bu da çevrəvi əşyaların populyarlığını artırır.
Memarlıqda isə dairəvi eyvanlar, günbəzlər və pəncərələr geniş istifadə olunur. Bu elementlər yalnız binaların gözəlliyini artırmır, həm də funksional olaraq dayanıqlıq yaradır. Beləliklə, gündəlik həyatımızda çevrə həm rahatlıq, həm də harmoniya rəmzi kimi qarşımıza çıxır.
Çevrənin riyazi əhəmiyyəti
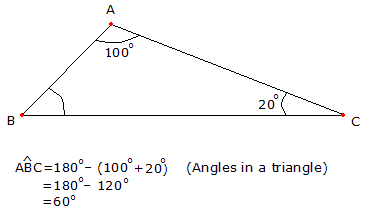
Riyaziyyatda çevrə müxtəlif teoremlərin əsasını təşkil edir. Məsələn, çevrədə bucaqların xassələri, qövsün uzunluğu və sektorun sahəsi kimi mövzular həm məktəb, həm də universitet proqramlarında geniş yer tutur. Çevrə üzərində qurulan məsələlər məntiqi təfəkkürün inkişafında mühüm rol oynayır.
Həmçinin trigonometrik funksiyaların əsası da vahid çevrə üzərində qurulmuşdur. Bu, yalnız riyazi nəzəriyyələrdə deyil, həm də fizikanın müxtəlif sahələrində tətbiq edilir. Çevrə riyaziyyatda həm sadə, həm də mürəkkəb problemlərin həlli üçün universal bir vasitədir.
Çevrə ilə bağlı maraqlı faktlar
Çevrənin ətrafını tam olaraq ədəd şəklində ifadə etmək mümkün deyil, çünki π irrasional ədəddir. Bu ədədin sonsuz onluq kəsri hələ də alimlər tərəfindən hesablanır. Bu fakt çevrənin həm sadə, həm də dərin bir riyazi obyekt olduğunu göstərir.
Bundan başqa, dünyanın müxtəlif mədəniyyətlərində çevrə mükəmməlliyin, sonsuzluğun və əbədiyyətin rəmzi sayılır. Bu baxımdan çevrə yalnız riyazi fiqur deyil, həm də fəlsəfi və simvolik məna daşıyır. Həyatın müxtəlif qatlarında bu rəmz insan təfəkkürünü zənginləşdirmişdir.
Çevrə insanın dünyanı anlamaq və dərk etmək səylərinin mühüm hissəsi olmuşdur. Onun sadə görünüşü arxasında böyük bir fəlsəfi və elmi dərinlik gizlənir. Riyaziyyatın ən fundamental mövzularından biri olaraq çevrə təbiətdə, texnologiyada, incəsənətdə və gündəlik həyatda öz əksini tapır. Mərkəz, radius, diametr və qövs kimi anlayışlar insanın məntiqi düşüncə tərzini formalaşdırır və elmi araşdırmalar üçün zəmin yaradır.
Cədvəl: Çevrənin əsas elementləri
| Anlayış | Tərif | Düstur və ya xüsusiyyət |
|---|---|---|
| Mərkəz | Çevrənin bütün nöqtələrinə eyni məsafədə olan nöqtə | — |
| Radius | Mərkəzdən çevrənin üzərinə qədər olan məsafə | r |
| Diametr | Çevrənin mərkəzindən keçən ən uzun düz xətt | d = 2r |
| Çevrənin uzunluğu | Çevrənin sərhədinin ölçüsü | C = 2πr |
| Dairənin sahəsi | Çevrə ilə məhdudlaşan sahə | S = πr² |
Çevrə yalnız riyazi düsturlarla ifadə edilən bir fiqur deyil, həm də həyatın özündə mövcud olan harmoniyanın və simmetriyanın simvoludur. Təbiətdəki formalar, mühəndislik həlləri, memarlıq əsərləri və incəsənət nümunələri onun universallığını bir daha sübut edir. İnsan zehni də bu simmetriyanı təbii olaraq qəbul edir və gündəlik fəaliyyətində tətbiq edir.Bəşəriyyətin minilliklər boyu çevrəni öyrənməsi və tətbiq etməsi göstərir ki, sadə formaların arxasında böyük həqiqətlər gizlənə bilər. Əslində çevrə həm məntiq, həm də gözəllik arasında körpü rolunu oynayır. Bu körpü elm ilə sənəti, təbiət ilə texnologiyanı birləşdirən mühüm elementdir. Çevrəni dərk etmək həm dünyanı anlamaq, həm də öz daxili harmoniyasını tapmaq deməkdir.
Ən Çox Verilən Suallar
Çevrə riyaziyyatda verilmiş mərkəzdən bərabər məsafədə olan bütün nöqtələrdən ibarət düz xəttdir.
Çevrə yalnız xətti, dairə isə bu xəttin içərisində olan sahəni ifadə edir.
Çevrənin uzunluğu L = 2πr düsturu ilə hesablanır, burada r – radiusdur.
Təkərlər, saatlar, bəzək əşyaları və bir çox texniki qurğular çevrə formasındadır.
Radius, diametr, mərkəz, bucaq, kəsik, toxunma və s.
Radius mərkəzdən hər hansı nöqtəyə qədər olan məsafədir, diametr isə iki nöqtə arasındakı ən uzun məsafədir və 2r-ə bərabərdir.
Çevrə əsasən həndəsə və cəbr fənlərində öyrənilir.
Çevrənin sahəsi əslində dairənin sahəsini bildirir və S = πr² düsturu ilə hesablanır.
Bəli, çevrə sözündən sosial mühit, insan qrupu və ya idarəetmə sahəsində də istifadə olunur.
Çevrə qədim dövrlərdən riyaziyyat və astronomiyada istifadə olunub və elmi inkişafa böyük təsir göstərib.