Kürə riyaziyyatda və təbiət elmlərində ən vacib üçölçülü fiqurlardan biri hesab olunur. Onun ideyası gündəlik həyatımızdan tutmuş, astronomiya, fizika, mühəndislik kimi sahələrə qədər geniş yayılan, universal bir formadır. İnsanlar qədimdən bəri kürə forması ilə maraqlanıb və bu formanın təbiətdə – Yer kürəsi, planetlər, damcılar, top və digər obyektlərdə necə təzahür etdiyini müşahidə ediblər. Kürə həm simmetrikliyi, həm də həcm və səthinin riyazi cəhətdən asan hesablana bilməsi ilə seçilir. Riyaziyyatın ən əsas məsələlərindən biri də müxtəlif formaların, o cümlədən kürənin həcm və səth sahəsinin hesablanması olub.
Kürənin həcminin hesablanması həm riyaziyyatçılar, həm də mühəndislər üçün vacib anlayışdır. Həcmin tapılması yalnız riyazi bilik üçün deyil, eyni zamanda, fizika, kimya, texnologiya və hətta gündəlik həyatımızda vacib rol oynayır. Məsələn, maye və qazların saxlanması üçün kürə formalı qablar, su damcılarının və ya idman toplarının ölçülməsi bu düstura əsaslanır. Riyaziyyatda isə bu düstur, stereometriya fənninin əsas hissələrindən biri kimi öyrədilir və digər mürəkkəb fiqurların həcm hesablanmasında istifadə olunur.
Kürənin həcm düsturu antik dövrlərdən bəlli idi və bir çox məşhur riyaziyyatçılar – Arximed, Eudoks, və başqaları tərəfindən araşdırılıb. Arximed hələ eramızdan əvvəl III əsrdə kürənin həcm və səth düsturunu sübut etmiş, bununla bəşər tarixində əlamətdar yer tutmuşdur. Bu düsturun tətbiqi müxtəlif sahələrdə ölçü, hesab, model qurmaq və analiz üçün əsas vasitələrdəndir. Ona görə də kürənin həcm düsturunu bilmək təkcə riyaziyyat müəllimlərinin deyil, eyni zamanda həyatla bağlı olan hər kəsin bilməsi vacib olan elmi biliklərdəndir.
Kürə nədir?
Kürə, bütün nöqtələri mərkəzdən bərabər məsafədə olan üçölçülü cisimdir. Riyaziyyatda kürə, öz mərkəzindən verilmiş radius qədər məsafədə yerləşən nöqtələr toplusu kimi müəyyən olunur. Kürə simmetrik formaya malikdir və hər bir istiqamətdə eyni ölçüyə sahibdir. Təbiətdə və gündəlik həyatda kürə forması tez-tez rast gəlinir: Yer kürəsi, su damcısı, top, bəzi meyvələr və s.
Kürənin əsas xüsusiyyəti, onun səthindəki hər bir nöqtənin mərkəzdən eyni məsafədə yerləşməsidir. Bu səbəbdən kürə simmetrik fiqurların ən təmiz forması hesab edilir və riyazi baxımdan öyrənilməsi çox əhəmiyyətlidir. Kürə həmçinin, müxtəlif elmlərdə modelləşdirmə və analiz məqsədilə tez-tez istifadə olunur.
Kürənin əsas parametrləri
Kürənin əsas parametrləri radius, diametr, çevrə, səth sahəsi və həcm kimi riyazi anlayışlardır. Radius – kürənin mərkəzindən onun səthindəki istənilən nöqtəyə qədər olan məsafədir. Diametr isə, mərkəzdən keçərək kürənin iki nöqtəsini birləşdirən düz xəttdir və radiusun ikiqatıdır. Çevrə isə, kürənin ən böyük dairəsinin uzunluğudur.
Kürənin səth sahəsi və həcmi isə riyazi düsturlarla asanlıqla hesablanır. Səth sahəsi kürənin xarici hissəsinin ümumi ölçüsünü göstərir, həcm isə kürənin daxilindəki məkanı, yəni üçölçülü “doldurulmuş” hissəni əks etdirir. Bu parametrlər istər riyaziyyat, istərsə də digər elmlər üçün əhəmiyyətlidir.
Kürənin həcmi nə deməkdir?
Kürənin həcmi, onun daxilində yerləşə bilən məkanın ölçüsüdür. Riyaziyyatda həcm üçölçülü fiqurlar üçün istifadə olunan əsas parametrlərdən biridir və litrlə, kub metr və ya digər həcm vahidləri ilə ölçülür. Məsələn, kürə formasında olan bir su çəni və ya qaz balonunun nə qədər maye və ya qaz tutacağını hesablamaq üçün məhz həcm düsturundan istifadə olunur.
Kürənin həcmi, onun radiusuna görə dəyişir və radiusun böyüməsi ilə eksponensial şəkildə artır. Yəni, radius bir qədər artırıldıqda, həcm daha sürətlə böyüyür. Bu, müxtəlif praktiki və elmi tətbiqlər üçün mühüm nəticələrə gətirib çıxarır.
Kürənin həcminin düsturu necə tapılıb?
Kürənin həcmi üçün istifadə olunan klassik düstur eramızdan əvvəl III əsrdə məşhur yunan riyaziyyatçısı Arximed tərəfindən tapılıb və sübut edilib. Arximed, eyni hündürlüyə və radiusa malik silindrin və kürənin həcmlərini müqayisə edərək, kürənin həcminin silindrin həcminin üçdə ikisinə bərabər olduğunu sübut edib. Bu elmi kəşf o dövr üçün inqilabi əhəmiyyət kəsb edirdi.
Arximedin verdiyi bu düstur daha sonra bir çox riyaziyyatçılar tərəfindən təkmilləşdirilib və bugünkü formada bütün dünya məktəblərində tədris olunur. Riyaziyyatda bu düstur stereometriyanın ən mühüm düsturlarından biri hesab edilir və üçölçülü fiqurların həcmini hesablamaq üçün baza kimi qəbul edilir.
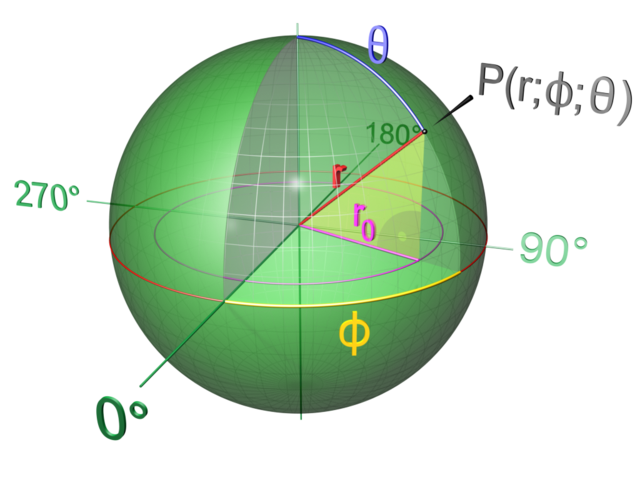
Kürənin həcmi düsturu
Kürənin həcmi aşağıdakı düsturla hesablanır:
V = (4/3) × π × r³
Burada V – kürənin həcmi, r – radius, π isə riyazi sabitdir (təxminən 3,1416). Yəni, kürənin radiusunu üç dəfə öz-özünə vurub, π ilə hasilini çıxarıb, onu da 4/3-ə vurmaqla həcm tapılır.
Bu düstur sayəsində müxtəlif ölçülü kürələrin, istər kiçik top, istərsə də nəhəng planetlərin həcmindən asanlıqla məlumat almaq mümkündür. Düsturun əsas üstünlüyü isə sadə olması və yalnız bir parametrə – radiusa əsaslanmasıdır.
Kürənin həcmi düsturunun tətbiqləri
Kürənin həcmi düsturu elmdə və gündəlik həyatda geniş istifadə olunur. Məsələn, kimya laboratoriyalarında kürə formalı balonların tutumunu, mühəndislikdə qaz və maye saxlama qablarının həcmini, hətta kosmosda planetlərin və ulduzların ölçülərini hesablamaq üçün bu düsturdan istifadə edilir. Riyaziyyatda isə müxtəlif hesablama məsələlərinin və modelləşdirmənin əsasını təşkil edir.
Eyni zamanda, bu düstur vasitəsilə təbiətdə və texnikada rast gəlinən hər bir kürəvi obyektin daxilində nə qədər məkan olduğunu müəyyən etmək mümkündür. Bu, həm də digər mürəkkəb fiqurların həcm hesablamalarında bazis rolunu oynayır.
Kürənin həcminin nümunə ilə hesablanması
Məsələn, radiusu 3 sm olan bir kürənin həcmini hesablamaq üçün düstura əsasən:
V = (4/3) × π × 3³ = (4/3) × π × 27 ≈ 113,1 sm³
Bu üsul istənilən radius üçün tətbiq oluna bilər. Təkcə riyaziyyat dərslərində deyil, real həyatda da bu cür hesablama modelləri vacibdir. Nümunədəki kimi sadə metodla, müxtəlif ölçülü kürələrin daxilində nə qədər məkan tutduğunu dəqiq hesablamaq olar.
Kürənin səth sahəsi ilə həcm arasındakı əlaqə
Kürənin səth sahəsi və həcm düsturları arasında birbaşa riyazi əlaqə var. Səth sahəsinin düsturu belədir:
S = 4 × π × r²
Hər iki düsturda radius əsas rolu oynayır və səth sahəsi ilə həcm arasında bir-birini tamamlayan riyazi əlaqə mövcuddur. Bu əlaqə sayəsində kürə ilə bağlı bütün əsas parametrlər asanlıqla hesablana bilir. Həm səth, həm də həcmin hesablanması elmi, texniki və gündəlik məsələlərin həllində zəruridir.
Kürənin həcminin gündəlik həyatda və elmdə rolu
Kürənin həcminin hesablanması gündəlik həyatda da geniş istifadə olunur. Məsələn, maye saxlanması üçün kürə formalı çənlər, idman toplarının ölçülməsi, fiziki təcrübələrdə balonların tutumu, tibbi cihazlarda istifadə olunan kürəvi hissələrin həcmi kimi müxtəlif sahələrdə bu biliklər vacibdir. Elmdə isə, kürəvi cisimlərin ölçülməsi astronomiya, fizika və kimya üçün fundamental əhəmiyyət daşıyır.
Cədvəl: Kürənin əsas parametrləri və düsturları
| Parametr | Təyinatı | Düstur | Ölçü vahidi |
|---|---|---|---|
| Radius (r) | Mərkəzdən səthə qədər məsafə | r | sm, m |
| Diametr (d) | İki qarşı tərəfdəki nöqtə arasındakı məsafə | d = 2r | sm, m |
| Səth sahəsi (S) | Kürənin xarici səthinin ölçüsü | S = 4 × π × r² | sm², m² |
| Həcm (V) | Kürənin daxilindəki məkan | V = (4/3) × π × r³ | sm³, m³ |
| Çevrə | Ən böyük dairənin uzunluğu | C = 2 × π × r | sm, m |
Kürənin həcmi və onun hesablanması, riyaziyyat və təbiət elmlərində fundamental anlayışlardan biridir. Həcmin düsturunu bilmək yalnız elmi tədqiqatlar üçün deyil, gündəlik praktikada da çox vacibdir. Sadə riyazi düsturla kürənin daxilində nə qədər məkan olduğunu asanlıqla hesablamaq mümkündür. Bu biliklər müxtəlif sahələrdə, texnikada, elm və gündəlik həyatda geniş tətbiq olunur. Kürənin həcminin və digər parametrlərinin hesablanması insanların dünyanı daha yaxşı dərk etməsi, ölçmə və idarəetmədə dəqiqliyin təmin olunması baxımından əvəzolunmaz rol oynayır. Kürə, həm öz forması, həm də riyazi xüsusiyyətləri ilə ən maraqlı və öyrədici fiqurlardan biri olaraq qalır.
Ən Çox Verilən Suallar
Kürənin həcm düsturu V = (4/3) × π × r³ formasındadır. Burada V – həcm, r – radius, π isə riyazi sabitdir (təxminən 3,1416).
Kürənin həcmini hesablamaq üçün əsasən onun radiusunu bilmək kifayətdir. Düsturda radiusun kubu əsas rol oynayır.
Kürənin səth sahəsi S = 4 × π × r² düsturu ilə, həcmi isə V = (4/3) × π × r³ düsturu ilə tapılır. Hər iki düsturda radius əsas parametrlərdən biridir.
Kürə – bütün nöqtələri mərkəzdən bərabər məsafədə olan üçölçülü fiqurdur. Riyaziyyatda və təbiətdə geniş istifadə olunur.
Kürənin diametri onun radiusunun iki misli olur, yəni d = 2r düsturuna əsasən tapılır.
Kürənin həcm düsturu eramızdan əvvəl III əsrdə yunan riyaziyyatçısı Arximed tərəfindən tapılmış və elmi cəhətdən sübut olunmuşdur.
Həcmi ölçmək üçün ən çox kub santimetr (sm³), kub metr (m³) və litr kimi vahidlərdən istifadə olunur.
Kürəvi cisimlərə idman topları, su və qaz çənləri, planetlər və bənzər bir çox obyektlər misal göstərilə bilər. Onların həcm hesablama düsturu eyni qaydada işləyir.
Kürənin radiusu böyüdükcə, həcm çox sürətlə artır. Radiusun bir qədər artması belə, həcmin böyük ölçüdə böyüməsinə səbəb olur.
Kürənin həcm düsturu, müxtəlif ölçülü cisimlərin, maye və qaz qablarının tutumunun, idman toplarının ölçüsünün və bir çox obyektin həcminin hesablamaq üçün gündəlik həyatda vacibdir.