Riyaziyyatın əsas bölmələrindən biri olan həndəsə insan düşüncəsinin formalaşmasında, əşyaların, təbiət və texniki proseslərin öyrənilməsində mühüm rol oynayır. Həndəsənin əsas anlayışları arasında bucaqlar xüsusi yer tutur. Bucaq həm gündəlik həyatda, həm texnologiyada, həm də təbiətdə müxtəlif formaların, istiqamətlərin və ölçülərin müəyyən edilməsində istifadə olunur. Bucaqların bir neçə növü olsa da, onların ən fundamental və çox istifadə edilən növlərindən biri qonşu bucaqlardır. Qonşu bucaqlar yalnız riyazi baxımdan deyil, həm də memarlıqda, mühəndislikdə, təbiət elmlərində və gündəlik məntiqi problemlərin həllində əhəmiyyətli yer tutur. Qonşu bucaqlar anlayışının düzgün mənimsənilməsi həm məktəb yaşlı uşaqlar, həm də riyaziyyatı peşəkar səviyyədə öyrənənlər üçün vacibdir.
Qonşu bucaqlar anlayışı, onun xassələri, riyazi dəlilləri və müxtəlif sahələrdə tətbiq imkanları bu mövzunun daim aktual və maraqlı qalmasına səbəb olur. Həmçinin qonşu bucaqlar üzərində aparılan məntiqi-müqayisəli təhlillər düşüncə qabiliyyətinin inkişafına böyük töhfə verir.
Qonşu bucaqların əsas anlayışı və tərifi
Qonşu bucaqlar eyni başlanğıc nöqtəsinə malik olan və bir tərəfi ortaq, digər tərəfləri isə müxtəlif istiqamətdə yerləşən iki bucağa deyilir. Riyazi dildə desək, bir nöqtədə iki şüanın ayrılmasından əmələ gələn iki bucağın bir tərəfi üst-üstə düşürsə, bu bucaqlar qonşu bucaqlar adlanır. Qonşu bucaqlar düz xətt üzərində əmələ gəlir və onların ümumi şüası (tərəfi) olur.
Qonşu bucaqlar üçün əsas tələblər aşağıdakılardır:
- Hər iki bucağın bir başlanğıc nöqtəsi (zirvəsi) olmalıdır
- Bir tərəfi ortaq olmalıdır
- Qalan tərəfləri bir-birindən fərqli olmalıdır
Bu anlayış həndəsənin təməl mövzularından biri olmaqla yanaşı, digər bucaq növlərinin, məsələn, tamamlayıcı, bərabər, qarşı, şaquli və sair bucaqların da öyrənilməsində baza rolunu oynayır.
Qonşu bucaqların riyazi və vizual tərifi
Qonşu bucaqların daha yaxşı başa düşülməsi üçün onları sadə bir riyazi təsvir və vizual nümunə ilə izah etmək olar. Tutaq ki, OO nöqtəsindən çıxan iki şüa — OAOA və OBOB — və əlavə olaraq üçüncü bir şüa OCOC var. Əgər OAOA və OBOB şüaları ilə əmələ gələn ∠AOB∠AOB və OBOB ilə OCOC şüası ilə əmələ gələn ∠BOC∠BOC bucaqları varsa, burada OBOB şüası ortaq tərəf rolunu oynayır. Beləliklə, ∠AOB∠AOB və ∠BOC∠BOC qonşu bucaqlar sayılır.
| Bucaq Növü | Tərifi | Vizual izah (şəklə baxın) |
|---|---|---|
| Qonşu bucaqlar | Bir ortaq tərəfi, bir ortaq zirvəsi, fərqli digər tərəfləri olan | İki bucaq, ortaq şüa |
| Şaquli bucaqlar | Zirvələri ortaq, tərəfləri bir-birinin əksi olan bucaqlar | Xaç şəkilli kəsişən şüalar |
Qonşu bucaqların əsas xassələri
Qonşu bucaqların bir neçə mühüm xassəsi var. Bu xassələr həm riyazi hesablama, həm də məntiqi analiz üçün vacibdir. Qonşu bucaqlar üçün əsas xassələr bunlardır:
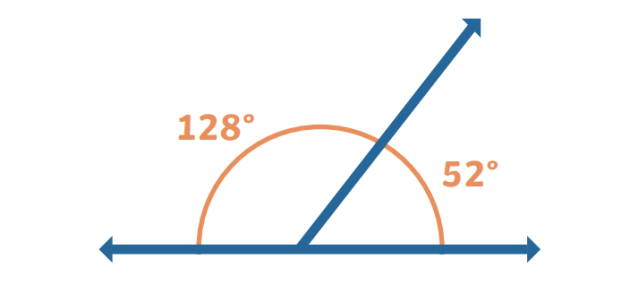
- Qonşu bucaqların cəmi, əgər onların digər tərəfləri bir düz xətt təşkil edirsə, 180°-yə bərabər olur. Belə bucaqlara düz bucaq da deyilir.
- Qonşu bucaqlar bir-birini tamamlayırsa, onların cəmi 90°-yə bərabər olur.
- Qonşu bucaqlarda bir bucaq artdıqda, digəri azalır və ya əksinə.
Bunları riyazi şəkildə aşağıdakı kimi ifadə etmək olar:Əgər ∠AOB+∠BOC=180∘, bu bucaqlar du¨z bucaqlar adlanır.Əgər ∠AOB+∠BOC=180∘, bu bucaqlar du¨z bucaqlar adlanır.Əgər ∠AOB+∠BOC=90∘, bu bucaqlar tamamlayıcı qons¸u bucaqlardır.Əgər ∠AOB+∠BOC=90∘, bu bucaqlar tamamlayıcı qons¸u bucaqlardır.
Qonşu bucaqların praktiki tətbiqləri
Qonşu bucaqlar yalnız nəzəri riyaziyyatda deyil, memarlıqda, inşaatda, mexanikada, elektronika və optikada geniş istifadə olunur. Məsələn, bina və körpü layihələndirərkən, konstruksiyaların dəqiq bucaqlarının hesablanması üçün qonşu bucaqlar konsepsiyasına ehtiyac yaranır. Elektron sxemlərdə, optik cihazların dizaynında da bu bucaqların düzgün hesablanması böyük əhəmiyyət kəsb edir.
Həmçinin gündəlik həyatda, məsələn, divar və döşəmə kəsişmələrində, yolayrıcılarında, bədii və sənət əsərlərinin yaradılmasında, həndəsi fiqurların qurulmasında qonşu bucaqlar prinsipi əsas alınır.
Qonşu bucaqlar və digər bucaq növləri ilə fərqləri
Qonşu bucaqlar bəzən şaquli və tamamlayıcı bucaqlarla qarışdırıla bilər. Ancaq əsas fərq ondadır ki, şaquli bucaqlar bir nöqtədə kəsişən iki düz xəttin əmələ gətirdiyi və bir-birinə qarşı olan bucaqlardır, onların tərəfləri əks istiqamətdə olur və həmişə bərabərdir. Qonşu bucaqlarda isə yalnız bir ortaq tərəf var və onlar bir-birinə bitişik yerləşir.
Aşağıdakı cədvəldə qonşu və digər bucaq növlərinin müqayisəsi verilib:
| Bucağın növü | Ortaq tərəf | Zirvə nöqtəsi | Tərəflərin yerləşməsi | Xüsusiyyət |
|---|---|---|---|---|
| Qonşu bucaqlar | Var | Var | Bitişik, bir şüa üst-üstə | Bitişik yerləşir |
| Şaquli bucaqlar | Yox | Var | Əks istiqamət | Qarşı bucaqlar bərabər |
| Tamamlayıcı bucaq | Var | Var | Cəmləri 90° | Qonşu da ola bilər |
Qonşu bucaqların hesablanması və nümunələr
Qonşu bucaqların ölçülərinin hesablanması riyaziyyatın əsas tapşırıqlarından biridir. Bu zaman bir bucağın ölçüsü məlumdursa və qonşu bucağın ölçüsü tapılmalıdırsa, əsas qayda budur: əgər düz bucaq təşkil edirsə, ikinci bucağı tapmaq üçün 180°-dən birinci bucağı çıxmaq kifayətdir.
Məsələn, əgər ∠AOB=70∘∠AOB=70∘, qonşu ∠BOC∠BOC tapmaq üçün:∠BOC=180∘−70∘=110∘∠BOC=180∘−70∘=110∘
Digər praktiki misal: Əgər iki qonşu bucağın biri 45°-dirsə və onların cəmi tamamlayıcıdırsa, ikinci bucaq 45°-dir.
Qonşu bucaqların öyrənilməsinin əhəmiyyəti
Qonşu bucaqların məntiqi öyrənilməsi məktəblilərin həndəsə üzrə düşüncə və məntiqini inkişaf etdirir, analitik bacarıqlarını gücləndirir. Həm də bu mövzunun dərin mənimsənilməsi digər həndəsi anlayışların (paralel, perpendikulyar, çoxbucaqlılar və s.) düzgün başa düşülməsi üçün baza rolunu oynayır. Qonşu bucaqlar mövzusu riyaziyyat olimpiadalarında, test imtahanlarında və məntiqi tapşırıqlarda tez-tez rast gəlinir.
Qonşu bucaqlar haqqında maraqlı faktlar
- Qonşu bucaqların cəmi həmişə düz bucaq təşkil edə bilər, lakin hər bir qonşu bucaq düz bucaq olmayacaq.
- Eyni düz xətt üzərində bir neçə qonşu bucaq ardıcıl yerləşə bilər və onların cəmi də ümumi bucağa bərabər olur.
- Qonşu bucaqlar prinsipindən istifadə olunmadan mürəkkəb çoxbucaqlılar və həndəsi fiqurların kənar və daxili bucaqları hesablamaq çətindir.
Qonşu bucaqların tapılmasında əsas səhvlərdən biri ortaq tərəfin düzgün seçilməməsidir. Həmçinin, bəzən qarşı və ya bərabər bucaqlarla qarışdırılır. Bu səbəbdən, hər zaman fiqurun riyazi modelini çəkmək və ortaq tərəfi dəqiq müəyyən etmək vacibdir. Vizual modeldən istifadə etmək, müxtəlif tapşırıqları yerinə yetirmək və praktik nümunələrlə çalışmaq bu səhvlərin qarşısını almaqda kömək edir.
Qonşu bucaqların tətbiqi və inkişafı
Müasir riyaziyyatda və tətbiqi elmlərdə qonşu bucaqlar anlayışı daim təkmilləşir və müxtəlif proqramlaşdırma, kompüter qrafikası, robot texnikası, dizayn və aerodinamika kimi sahələrdə geniş istifadə edilir. Yeni texnologiyaların yaranması ilə bu konsept daha mürəkkəb həndəsi və analitik məsələlərin həllində vacib amilə çevrilir.
Qonşu bucaqlar həndəsənin və riyaziyyatın əsas anlayışlarından biridir. Onların xassələrinin və riyazi prinsiplərinin dərindən öyrənilməsi həm gündəlik həyatda, həm də elmi-texniki fəaliyyətdə uğur qazanmaq üçün vacibdir. Qonşu bucaqlar məntiqi və analitik düşüncənin inkişafı, riyazi problemlərin həlli və müasir texnologiyada tətbiq baxımından Azərbaycan cəmiyyəti üçün də böyük əhəmiyyət kəsb edir.
Ən Çox Verilən Suallar
Qonşu bucaqlar bir ortaq zirvəyə və bir ortaq tərəfə malik olan, digər tərəfləri isə müxtəlif istiqamətlərdə olan iki bucağa deyilir.
Əgər qonşu bucaqlar bir düz xətt üzərində yerləşirsə, onların cəmi həmişə 180° olur. Tamamlayıcı qonşu bucaqların cəmi isə 90°-dir.
Qonşu bucaqlar divar və döşəmə kəsişmələrində, yolayrıcılarında, tikintidə, memarlıqda və çoxbucaqlı fiqurların qurulmasında rast gəlinir.
Qonşu bucaqlarda bir ortaq tərəf və zirvə var, şaquli bucaqlarda isə ortaq tərəf yoxdur, yalnız zirvə birgədir və onlar həmişə bərabər olur.
Əgər iki qonşu bucağın cəmi düz bucaq təşkil edirsə, birinin ölçüsünü tapmaq üçün 180°-dən digərini çıxmaq kifayətdir.
Əsas səhv qonşu və şaquli bucaqları qarışdırmaq, ortaq tərəfi düzgün müəyyən etməməkdir. Vizual model çəkmək səhvlərin qarşısını alır.
Bu anlayış həndəsə dərslərində digər bucaq növlərinin və fiqurların öyrənilməsində baza rolunu oynayır və məntiqi düşüncəni inkişaf etdirir.
Memarlıq, inşaat, mühəndislik, kompüter qrafikası, robot texnikası və optika kimi sahələrdə qonşu bucaqların hesablanması vacibdir.
Bəli, qonşu bucaqlar tamamlayıcı və düz bucaqlarla sıx bağlıdır, bəzən digər bucaq növlərinin tapılmasında açar rol oynayır.
Əsas üsul – verilən bucağın ölçüsünü ümumi bucaqdan çıxmaqdır; praktikada isə riyazi modellər, riyazi düsturlar və həndəsi cizgilərdən istifadə edilir.