Qövs və mərkəzi bucaq anlayışları riyaziyyatın həndəsə bölməsində xüsusi yer tutur. Dairənin bir hissəsini təyin etmək, onun uzunluğunu və sahəsini hesablamaq üçün mərkəzi bucaq və qövs terminləri birmənalı əhəmiyyət daşıyır. Dairə üzərində istənilən iki nöqtə seçildikdə, bu nöqtələrdən keçən əyri parça “qövs” adlanır və həmin qövsə uyğun olaraq dairənin mərkəzində əmələ gələn bucaq “mərkəzi bucaq” kimi qəbul edilir. Hər bir dairədə qövs və mərkəzi bucaq arasında riyazi əlaqə var. Bu əlaqə həm dairənin ümumi sahəsinin, həm də konkret qövsə uyğun sahənin hesablama üsullarının əsasını təşkil edir. Məktəb proqramlarında bu anlayışlara xüsusi diqqət yetirilir, çünki riyazi və məntiqi təfəkkürün inkişafı üçün qövs və mərkəzi bucaq mövzuları əsasdır. Mərkəzi bucaq həm də digər həndəsi fiqurlarda, xüsusilə çoxbucaqlılarda, simmetrik konstruksiyalarda və texniki çertyojlarda istifadə edilir. Bütün bu mövzunun dərindən öyrənilməsi real həyatda texniki layihələrin qurulmasında, memarlıqda, mühəndislikdə və gündəlik praktikada vacib bacarıqlar qazandırır. Qövs və mərkəzi bucaq həm nəzəri, həm də praktiki məsələlərin əsas komponentləri kimi çıxış edir. Onların öyrədilməsi zamanı vizual təsvirlərdən və praktiki tapşırıqlardan istifadə olunması bu mövzunun başa düşülməsini asanlaşdırır. Bu anlayışlar həmçinin riyaziyyatın digər bölmələri, məsələn, trigonometriya və analitik həndəsə ilə sıx əlaqəlidir. Qövs və mərkəzi bucaq haqqında biliklərin tətbiqi insanların məkan düşüncəsini və analitik yanaşmasını artırır. Riyazi elmlər arasında bu mövzu öz aktuallığını heç vaxt itirmir və daim yeni tətbiq sahələri qazanır.
Qövs Anlayışı Və Onun Riyazi Təsviri
Qövs, dairənin iki nöqtəsi arasında çəkilən əyri parça kimi başa düşülür. Hər dairənin üzərində istənilən iki nöqtə seçildikdə, bu nöqtələr arasındakı ən qısa məsafə deyil, dairənin səthində uzanan əyri bir hissə yaranır və bu qövs adlanır. Qövs uzunluğu dairənin radiusu və mərkəzi bucağı ilə birbaşa əlaqəlidir.
Qövs uzunluğu riyazi formul vasitəsilə hesablana bilər. Əgər mərkəzi bucaq dərəcə ilə verilibsə, qövs uzunluğu L = 2·π·r·α/360 formulası ilə tapılır. Burada r – radius, α isə mərkəzi bucaqdır. Qövs uzunluğunun hesablanması müxtəlif sahələrdə, o cümlədən memarlıqda və mexanikada mühüm rol oynayır.
Mərkəzi Bucağın Mahiyyəti
Mərkəzi bucaq, dairənin mərkəzindən çəkilən iki şüa arasında qalan bucaqdır. Hər bir mərkəzi bucaq birbaşa dairənin mərkəz nöqtəsinə əsaslanır və həmin bucağa uyğun qövs dairə üzərində müəyyən bir hissəni əhatə edir. Mərkəzi bucağın ölçüsü, dairənin hansı hissəsinin nəzərdə tutulduğunu müəyyən edir.
Mərkəzi bucaq adətən dərəcə və ya radianla ifadə olunur. Tam dairə 360° və ya 2π radian qəbul edilir. Mərkəzi bucağın ölçüsünə görə qövsün uzunluğu və sektorun sahəsi dəqiq hesablana bilər. Bu, həm məktəb dərslərində, həm də peşəkar tətbiqlərdə geniş istifadə olunan mühüm anlayışdır.
Qövs Və Mərkəzi Bucağın Əlaqəsi
Qövs və mərkəzi bucaq arasında birbaşa riyazi münasibət mövcuddur. Dairənin istənilən hissəsi, seçilən mərkəzi bucaq əsasında hesablana bilər. Qövsün uzunluğu mərkəzi bucağa birbaşa proporsionaldır; yəni, bucaq artdıqca qövsün uzunluğu da artır.
Bu münasibət, qövs uzunluğunun hesablanmasında əsas rol oynayır. Mərkəzi bucaq dərəcə ilə verildikdə, qövs uzunluğunun dairənin ümumi çevrəsinə nisbəti α/360 olur. Eyni qayda ilə, radianla hesablama zamanı nisbət α/2π olaraq götürülür. Bu əlaqə riyazi məsələlərin həllində əsasdır.
Qövsün Riyazi Formulları
Qövsün uzunluğunu hesablamaq üçün bir neçə fərqli formula mövcuddur. Əgər mərkəzi bucaq dərəcə ilə verilmişsə, L = 2·π·r·α/360, əgər radianla verilmişsə, L = r·α formulundan istifadə olunur. Hər iki halda, radius və mərkəzi bucaq əsas rol oynayır.
Bəzi hallarda, qövsün uzunluğunu tapmaq üçün əvvəlcə bucağı dərəcədən radiana çevirmək tələb olunur. Bunun üçün α (dərəcə) × π/180 ifadəsi tətbiq edilir. Bu çevrilmə xüsusilə fizika və texniki riyaziyyat məsələlərində vacibdir.
Mərkəzi Bucağın Praktiki Tətbiqləri
Mərkəzi bucaq anlayışı yalnız riyaziyyat dərsliklərində deyil, gündəlik həyatda və texniki peşələrdə də geniş tətbiq olunur. Məsələn, yol döngələrinin layihələndirilməsində, körpü və tunel konstruksiyalarında mərkəzi bucaq anlayışından istifadə edilir. Hər bir dairəvi obyektin planlaşdırılması zamanı bucaqların ölçüləri vacib parametrdir.
Memarlıqda və mühəndislikdə mərkəzi bucağın dəqiq hesablanması tikinti obyektlərinin sabitliyini və funksionallığını təmin edir. Həmçinin, mexaniki qurğularda və fırlanma hərəkətinin analizində də mərkəzi bucaq anlayışı xüsusi əhəmiyyət daşıyır.
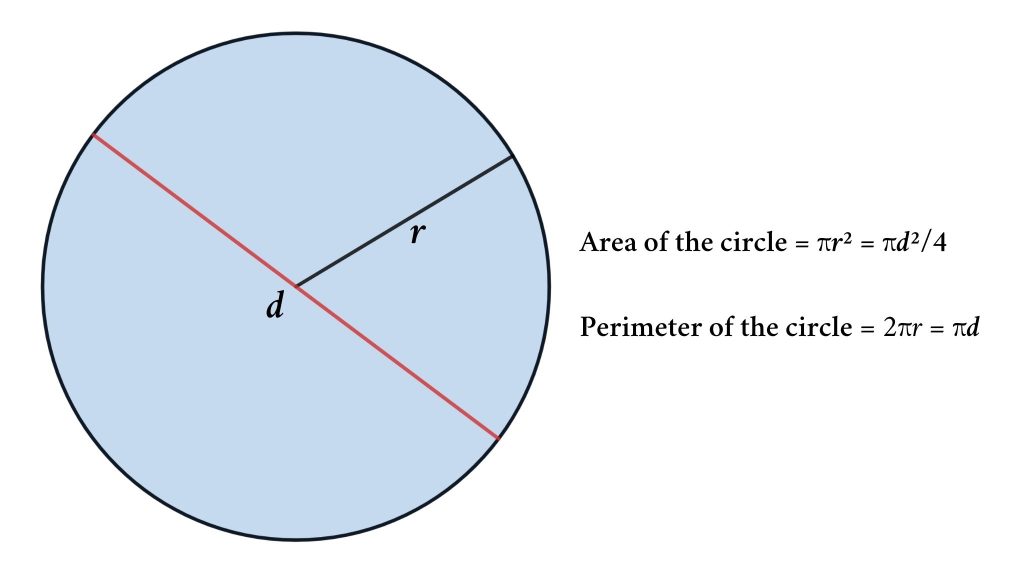
Qövsün Və Sektorun Sahəsinin Hesablanması
Qövsə uyğun sektorun sahəsi dairənin tam sahəsinin bir hissəsini təşkil edir. Əgər dairənin radiusu r və mərkəzi bucağı α dərəcədirsə, sektorun sahəsi S = π·r²·α/360 formulası ilə tapılır. Radianla verilmiş bucaq üçün S = (r²·α)/2 formulu tətbiq olunur.
Qövsün uzunluğu və sektorun sahəsi arasındakı əlaqə real həyatda çoxsaylı məsələlərin həllində istifadə olunur. Bu formullar sayəsində istənilən dairəvi hissənin sahəsini və ya uzunluğunu dəqiq hesablamaq mümkündür. Bu bilik memarlıqda, mühəndislikdə və riyazi modelləşdirmədə böyük əhəmiyyət daşıyır.
Qövs Və Mərkəzi Bucağın Tədrisində Yanaşmalar
Məktəblərdə və ali təhsil müəssisələrində qövs və mərkəzi bucaq mövzuları vizual alətlər və praktiki tapşırıqlarla öyrədilir. Kompas və bucaqölçən kimi alətlər şagirdlərə bu anlayışları daha aydın başa düşməyə imkan verir. Riyazi məsələlərin həllində praktiki nümunələr və illüstrasiyalardan istifadə geniş yayılmışdır.
Müəllimlər şagirdlərə qövs və mərkəzi bucaq anlayışlarını fərqli kontekstlərdə tətbiq etməyi öyrədirlər. İctimai layihələrdə, memarlıq planlarında və mühəndis hesabatlarında bu mövzunun əhəmiyyəti vurğulanır. Bu, şagirdlərin məntiqi və məkan təfəkkürünü gücləndirir.
Qövs Və Mərkəzi Bucağın Digər Elmlərdə İstifadəsi
Qövs və mərkəzi bucaq yalnız riyaziyyatda deyil, fizika, astronomiya, coğrafiya və hətta biologiyada da istifadə olunur. Astronomiyada göy cisimlərinin trayektoriyası, fizika dərslərində isə fırlanan obyektlərin hərəkət trayektoriyası bu anlayışlar vasitəsilə izah edilir. Coğrafiyada isə ərazilərin xəritəyə köçürülməsi zamanı bu biliklərdən istifadə olunur.
Həmçinin, texnologiya və qrafik dizayn sahəsində də dairəvi obyektlərin təsvirində qövs və mərkəzi bucaq vacibdir. Müasir proqram təminatlarında bu anlayışlardan istifadə etməklə animasiyalar, planlar və layihələr hazırlanır. Bu, elmin və texnikanın bir çox sahəsində qövs və mərkəzi bucaq anlayışının aktuallığını göstərir.
| Qövs, Mərkəzi Bucaqlar Və Formulları | Əsas Məlumatlar |
|---|---|
| Qövs uzunluğu (dərəcə ilə) | L = 2·π·r·α/360 |
| Qövs uzunluğu (radianla) | L = r·α |
| Sektor sahəsi (dərəcə ilə) | S = π·r²·α/360 |
| Sektor sahəsi (radianla) | S = (r²·α)/2 |
| Tam dairədə mərkəzi bucaq | 360° və ya 2π radian |
| Radius | Dairənin mərkəzindən qövsə qədər məsafə |
| Mərkəzi bucaq | Dairə mərkəzindən çıxan iki şüa arasında |
| Dərəcə və radian çevrilməsi | α (dərəcə) × π/180 = α (radian) |
Qövs və mərkəzi bucaq riyaziyyatın və həndəsənin təməl anlayışlarındandır. Bu anlayışlar sayəsində dairənin müxtəlif hissələri, onların uzunluğu və sahəsi asanlıqla hesablanır. Dairə üzərində iki nöqtə arasındakı əyri parça və bu parçada mərkəzdə əmələ gələn bucaq arasında riyazi əlaqə insanların məkan təsəvvürünü zənginləşdirir. Mərkəzi bucağın ölçüsünə görə həm qövsün uzunluğu, həm də sektorun sahəsi dəqiq tapılır. Bu, memarlıq, mühəndislik, astronomiya və digər elmi sahələrdə müxtəlif problemlərin həllini asanlaşdırır. Riyaziyyat təhsilində bu mövzunun dərin öyrədilməsi şagirdlərin analitik və məntiqi bacarıqlarını inkişaf etdirir. Qövs və mərkəzi bucaq texniki çertyojların hazırlanmasında, layihə və dizayn proseslərində, hətta gündəlik həyatın müxtəlif sahələrində aktualdır. Bu biliklər insanın dünyanı riyazi və məkan baxımından daha yaxşı başa düşməsinə kömək edir. Riyazi formulların düzgün tətbiqi və verilən məlumatların dəqiq təhlili doğru nəticələr əldə etməyə imkan verir. Hər bir dairəvi obyektin xüsusiyyətlərini anlamaq üçün qövs və mərkəzi bucaq anlayışlarının mənimsənilməsi vacibdir. Gələcəkdə də bu biliklərin aktuallığını və əhəmiyyətini qoruyacağı şübhəsizdir.
Ən Çox Verilən Suallar
Qövs, dairənin iki nöqtəsi arasında çəkilən əyri parça kimi təsvir edilir. O, dairənin bir hissəsini əhatə edir və radius, eləcə də mərkəzi bucaq vasitəsilə müəyyən olunur. Qövsün uzunluğu dairənin mərkəzi bucağı ilə birbaşa əlaqəlidir. Hər qövsün özünəməxsus uzunluğu və bucağı var.
Mərkəzi bucaq, dairənin mərkəzindən çıxan iki şüa arasında qalan bucaqdır. Bu bucaq dairənin üzərində müəyyən bir hissəni və ya qövsü təyin edir. Mərkəzi bucaq həm dərəcə, həm də radianla ifadə olunur. Tam dairədə mərkəzi bucaq 360° və ya 2π radian olur.
Qövsün uzunluğu mərkəzi bucaq və radius ilə birbaşa bağlıdır. Bucağın ölçüsü artdıqca qövsün uzunluğu da artır. Riyaziyyatda bu iki anlayış bir-birindən ayrılmazdır. Onlar dairənin hər hansı hissəsinin ölçülməsində istifadə olunur.
Əgər mərkəzi bucaq dərəcə ilə verilibsə, qövsün uzunluğu L = 2·π·r·α/360 formulası ilə tapılır. Əgər radianla verilibsə, L = r·α formulundan istifadə olunur. Burada r – radius, α isə mərkəzi bucaqdır. Hesablamalarda verilən vahidlərə diqqət etmək vacibdir.
Sektorun sahəsi dərəcə ilə verilmiş bucaq üçün S = π·r²·α/360, radian üçün isə S = (r²·α)/2 formulası ilə tapılır. Hər iki formulda r – radius, α isə uyğun olaraq dərəcə və ya radianla göstərilmiş bucaqdır. Sektor sahəsinin tapılması həm riyazi, həm də texniki məsələlərdə istifadə olunur.
Məktəblərdə kompas, bucaqölçən və vizual modellərdən istifadə edilir. Şagirdlər dairədə nöqtələr seçərək qövs və mərkəzi bucaq anlayışını praktiki nümunələrlə mənimsəyirlər. Riyazi məsələlərin həllində formullardan istifadə olunur. Praktiki tapşırıqlar şagirdlərin mövzunu daha yaxşı başa düşməsinə kömək edir.
Qövs və mərkəzi bucaq memarlıqda, mühəndislikdə, fizika, astronomiya və dizaynda geniş tətbiq olunur. Məsələn, körpülərin, stadionların və texniki obyektlərin layihələndirilməsində bu anlayışlardan istifadə edilir. Həmçinin, xəritəçəkmə və coğrafi analizlərdə də bu biliklər vacibdir. Bütün bunlar onların universallığını göstərir.
Ən çox rast gəlinən səhvlərdən biri dərəcə və radian arasında çevirmə səhvidir. Bəzən radiusun və ya bucağın vahidi düzgün seçilmir. Qövs uzunluğunun hesablanmasında formullardan düzgün istifadə etmək lazımdır. Verilənləri diqqətlə oxumaq dəqiq nəticə əldə etməyə kömək edir.
Bu anlayışlar riyaziyyatla yanaşı fizika, astronomiya, coğrafiya, biologiya, memarlıq və mühəndislikdə istifadə olunur. Astronomiyada planetlərin trayektoriyası, memarlıqda dairəvi obyektlərin planlaşdırılması üçün vacibdir. Bu, elmlərarası aktuallığı və tətbiq genişliyini göstərir. Bütün bu sahələrdə qövs və mərkəzi bucaq əsas rol oynayır.
Gündəlik həyatda, xüsusilə texniki sahələrdə dairəvi obyektlərin ölçülməsi və planlaşdırılması üçün bu biliklər vacibdir. Avtomobil yollarında döngələrin layihələndirilməsində, stadionların və parkların planlaşdırılmasında geniş istifadə olunur. Mərkəzi bucağın və qövsün dəqiq ölçülməsi etibarlı və funksional layihələrin icrası üçün əsas şərtdir. Riyazi biliklərin praktikada tətbiqi həyatımızı asanlaşdırır.