Funksiyaların analizi müasir riyaziyyatın və onun tətbiq sahələrinin əsasını təşkil edən ən vacib anlayışlardan biridir. Bir çox elmi və texniki problemlərin həllində, iqtisadi modellərdə, fiziki proseslərin öyrənilməsində funksiyaların davranışı və onların xüsusiyyətləri xüsusi yer tutur. Bu baxımdan, funksiyanın böhran nöqtəsi riyazi təhlilin ən həssas məqamlarından sayılır. Böhran nöqtəsi funksiyanın dəyişmə xarakterində əsaslı dönüşün baş verdiyi nöqtə kimi qiymətləndirilir və bu nöqtələr funksiyanın qrafikində kəskin dəyişiklik, yeni tendensiyanın başlanğıcı və ya vacib hadisələrin baş verdiyi məqamlar kimi çıxış edir.
Bu anlayışın düzgün başa düşülməsi təkcə riyaziyyat üçün deyil, eyni zamanda texniki sahələrdə optimal qərarların verilməsi üçün də vacibdir. Məsələn, istehsal proseslərinin planlaşdırılması, maliyyə bazarlarının analizi, mexaniki sistemlərin idarə olunması, hətta ekoloji modellərin hazırlanması zamanı böhran nöqtələrinin öyrənilməsi və düzgün qiymətləndirilməsi birbaşa nəticələrin dəqiqliyini təmin edir. Funksiyanın böhran nöqtəsində dəyişmə sürətinin ya sıfıra bərabər olması, ya da ümumiyyətlə mövcud olmaması, həmin nöqtənin xüsusi statusunu göstərir.
Böhran nöqtələri, adətən, lokal maksimum, lokal minimum və infleksiya nöqtələri kimi təsnif edilir. Hər bir növ özündə funksiyanın qiymətində və ya istiqamətində əsaslı dəyişiklik ehtiva edir. Bu nöqtələrin düzgün təyini və analizi üçün riyazi əsasların möhkəm olması, xüsusilə törəmə və ikinci törəmə anlayışlarının dərindən öyrənilməsi lazımdır. Beləliklə, funksiyanın böhran nöqtəsi yalnız akademik maraq üçün deyil, gündəlik həyatda rast gəlinən bir çox praktiki məsələlərin düzgün həllində də ayrılmaz rol oynayır. Mövzunun aktuallığı və geniş tətbiq imkanları onu həm şagirdlər, həm də mütəxəssislər üçün daim maraqlı və vacib saxlayır.
Funksiyanın Qrafiki və Davranışı
Funksiya dəyişənin hər bir qiymətinə uyğun bir nəticə verən xüsusi qaydadır. Funksiyanın qrafiki isə həmin uyğunluğun vizual təsviridir. Qrafik vasitəsilə funksiyanın necə dəyişdiyini, hansı aralıqlarda artdığını və ya azaldığını, hansı nöqtələrdə istiqamətini dəyişdiyini asanlıqla müşahidə etmək mümkündür.
Qrafikin xüsusiyyətləri arasında ən vacib məqamlardan biri, məhz qrafikdəki dönüş nöqtələrinin müəyyənləşdirilməsidir. Belə nöqtələrdə funksiya ya enişdən yoxuşa, ya da əksinə keçir və bu dəyişikliklər funksiyanın böhran nöqtələri adlanır. Qrafikdə bu nöqtələr adətən kəskin dönmə, əyriliyin dəyişməsi və ya kəsilmə kimi vizual fərqlənir. Bu xüsusiyyətlər funksiyanın analizində başlıca rola malikdir.
Qrafikdə böhran nöqtəsi axtararkən funksiyanın lokal maksimumu, lokal minimumu və infleksiya nöqtələri xüsusi əhəmiyyət daşıyır. Qrafikin bu nöqtələrində funksiyanın törəməsi sıfıra bərabər olur və ya ümumiyyətlə mövcud olmur. Bu isə həmin nöqtələrin funksiyanın ümumi davranışında əsaslı rol oynadığını göstərir.
Böhran Nöqtəsinin Məğzi
Funksiyanın böhran nöqtəsi, onun dəyişmə xarakterinin birdən-birə dəyişdiyi və ya qeyri-müəyyənlik yarandığı nöqtədir. Bu nöqtədə funksiyanın törəməsi sıfıra bərabər olur və ya mövcud olmur. Yəni, dəyişən artdıqca funksiyanın qiyməti bir istiqamətdə dəyişirsə, böhran nöqtəsində bu istiqamət kəskin şəkildə dəyişir.
Belə nöqtələr həm ekstremum (maksimum və minimum), həm də infleksiya nöqtələri ola bilər. Böhran nöqtəsi funksiyanın qrafikində istiqamət və əyrilik dəyişikliyi ilə müşahidə edilir. Bu nöqtənin tapılması üçün riyazi üsullardan – əsasən törəmə və ikinci törəmədən – istifadə edilir. Böhran nöqtələrinin təyini müxtəlif tətbiqi sahələrdə optimal həllərin tapılması üçün vacibdir.
Böhran nöqtəsində bəzən funksiya tərs çevrilir, yəni artım azalmaya və ya əksinə keçir. Həmçinin, infleksiya nöqtəsində əyrilik dəyişir, yəni qrafik bir istiqamətdən digərinə keçir. Bu cür dəyişikliklər funksiyanın real tətbiq sahələrində nəticəyə birbaşa təsir edir.
Böhran Nöqtələrinin Növləri
Funksiyanın böhran nöqtələri əsasən üç yerə bölünür: lokal maksimum, lokal minimum və infleksiya nöqtəsi. Lokal maksimum nöqtəsində funksiya yaxın ətrafında ən yüksək qiyməti alır. Lokal minimum nöqtəsində isə ən aşağı qiymətə çatır. Hər iki halda, funksiyanın törəməsi sıfıra bərabər olur, amma ikinci törəmənin işarəsi bu nöqtələrin fərqlənməsini təmin edir.
İnfleksiya nöqtəsində isə funksiyanın qrafikində əyriliyin istiqaməti dəyişir. Burada ikinci törəmə sıfıra bərabər olur, amma əyriliyin istiqamətinin dəyişməsi üçün üçüncü törəmə də nəzərə alınır. İnkişaf etmiş analizdə infleksiya nöqtəsinin düzgün təyini üçün bir neçə riyazi şərt yoxlanılır. Bu növlərin hər biri funksiyanın qrafikində və praktiki tətbiqlərdə özünəməxsus əhəmiyyət kəsb edir.
Böhran Nöqtələrinin Riyazi Təyini
Funksiyanın böhran nöqtəsini tapmaq üçün ilk addım funksiyanın törəməsini hesablamaqdır. Əgər funksiyanın törəməsi müəyyən nöqtədə sıfıra bərabərdirsə və ya ümumiyyətlə mövcud deyilsə, həmin nöqtə böhran nöqtəsi kimi qəbul oluna bilər. Bu nöqtələrin dəqiq təsnifatı üçün ikinci törəmə də analiz edilir.
Maksimum və minimum nöqtələrin təyinində ikinci törəmənin işarəsinə baxılır. Əgər ikinci törəmə mənfidirsə, nöqtə maksimum, müsbətdirsə minimum sayılır. İnfleksiya nöqtəsində isə ikinci törəmə sıfır olur və üçüncü törəmə sıfırdan fərqli olmalıdır. Böhran nöqtələrinin riyazi təyini funksiyanın tam analizini aparmaq üçün əsas şərtdir.
Böhran Nöqtələrinin Real Tətbiqləri
Böhran nöqtələrinin praktiki tətbiqi çox genişdir. İqtisadiyyatda tələbat və təklifin kəsişmə nöqtələri, bazarda qiymətlərin dəyişmə nöqtələri, istehsalatda məhsuldarlığın ən yüksək və ya ən aşağı nöqtəsi, hətta ətraf mühit dəyişikliklərinin kəskinləşdiyi məqamlar böhran nöqtəsi kimi qiymətləndirilir.
Həmçinin, mühəndislikdə və texnologiyada avtomatlaşdırılmış sistemlərin optimallaşdırılmasında, proseslərin idarə olunmasında, qrafik və şəkil emalında, hətta təbii fəlakətlərin proqnozlaşdırılmasında böhran nöqtələri əsas analiz aləti rolunu oynayır. Böhran nöqtələrinin düzgün təyini və təhlili nəticələrin etibarlılığını artırır, risklərin və itkilərin qarşısının alınmasında əsaslı rol oynayır.
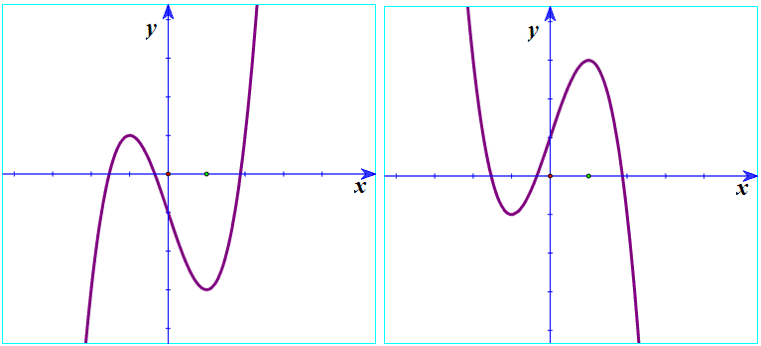
Böhran Nöqtəsi və Qrafikdə Vizual Təsviri
Funksiyanın böhran nöqtəsini vizual olaraq başa düşmək üçün qrafikinə baxmaq kifayətdir. Böhran nöqtəsində qrafikin istiqaməti və ya əyriliyi dəyişir. Qrafikdə lokal maksimum və minimum nöqtələrdə zirvə və ya çökəklik yaranır. İnfleksiya nöqtəsində isə qrafikin əyrilik istiqaməti bir yandan digərinə keçir.
Vizual olaraq böhran nöqtələri qrafikdə nəzərəçarpacaq dəyişikliklər yaradır və bu nöqtələrin yeri və sayı funksiyanın xüsusiyyətlərindən asılı olaraq dəyişə bilər. Funksiya nə qədər mürəkkəbdirsə, bir o qədər çox böhran nöqtəsinə malik ola bilər. Analitik metodların yanaşı, qrafik analiz də böhran nöqtələrinin təyinində effektivdir.
Riyazi Nümunə və Cədvəl
Bir funksiya üzərində böhran nöqtəsinin tapılması prosesini aşağıdakı cədvəldə əyani göstərmək mümkündür.
| Funksiya | Törəmə | Törəmənin sıfır olduğu nöqtələr | İkinci Törəmə | Böhran nöqtəsinin tipi |
|---|---|---|---|---|
| f(x) = x² – 4x + 3 | f'(x) = 2x – 4 | x = 2 | f”(x) = 2 | Minimum |
| f(x) = -x² + 6x – 5 | f'(x) = -2x + 6 | x = 3 | f”(x) = -2 | Maksimum |
| f(x) = x³ | f'(x) = 3x² | x = 0 | f”(x) = 6x | İnfleksiya |
Bu cədvəl vasitəsilə funksiyanın böhran nöqtəsi addım-addım necə tapılır, növü necə təyin edilir, aydın şəkildə görmək mümkündür.
Böhran Nöqtəsinin Tədrisdə və Elm Sahəsində Rolu
Böhran nöqtəsi anlayışı orta və ali məktəb proqramlarının ayrılmaz hissəsidir. Riyaziyyat dərslərində bu mövzu üzərində geniş dayanılır, çünki törəmə və ikinci törəmə anlayışlarının əsas tətbiq sahəsi məhz buradadır. Şagirdlər və tələbələr funksiyanın davranışını öyrənərkən, böhran nöqtələrinin təyini üzərində xüsusi dayanırlar.
Elmi-tədqiqat işlərində, proqramlaşdırma, data analitikası, iqtisadi modellər və tətbiqi riyaziyyat sahəsində böhran nöqtələrinin analizi tez-tez aparılır. Bu, müasir cəmiyyətin ehtiyaclarına cavab verən elmi bilik və bacarıqların inkişafına xidmət edir.
Böhran Nöqtəsinin İdentifikasiyasında Yaranan Çətinliklər
Praktikada bəzi funksiyaların böhran nöqtələrinin təyini mürəkkəb ola bilər. Mürəkkəb funksiyalarda törəmə və ikinci törəmənin analitik şəkildə tapılması, sıfıra bərabər olma şərtinin həll edilməsi və nöqtənin düzgün təsnifatı üçün əlavə riyazi biliklər tələb olunur.
Eyni zamanda, bəzi funksiyalarda bir nöqtədə həm maksimum, həm də minimum olmaya bilər, ya da funksiyanın törəməsi o nöqtədə mövcud olmaya bilər. Belə hallarda əlavə üsullardan, qrafik analiz və limitlərdən istifadə olunur. Çətinliklərə baxmayaraq, funksiyanın böhran nöqtələrinin düzgün təyini nəticələrin etibarlılığını və dəqiqliyini təmin edir.
Müasir Analizdə Böhran Nöqtələrinin Əhəmiyyəti
Riyazi analiz sahəsində böhran nöqtələrinin əhəmiyyəti getdikcə artır. Müasir hesablama və statistik metodlar, süni intellekt modelləri, data mining və maşın öyrənməsi kimi yeni sahələrdə funksiyaların böhran nöqtələri müxtəlif qərar mexanizmlərinin qurulmasında əsas rol oynayır.
Texnologiyanın inkişafı ilə böhran nöqtələrinin təhlili daha sürətli və dəqiq aparılır. Bununla yanaşı, nəzəri riyaziyyat və tətbiqi sahələr arasında körpü yaradılır. Bu da yeni elmi kəşflərə, iqtisadi və texnoloji inkişaflara səbəb olur.
Funksiyaların böhran nöqtəsi riyazi analiz və onun tətbiq sahələri üçün fundamental əhəmiyyət daşıyır. Bu nöqtələr funksiyanın davranışında əsaslı dəyişikliklərin baş verdiyi məqamlar olaraq optimal qərarların verilməsi üçün vacibdir. Hər bir şagird və mütəxəssis üçün böhran nöqtəsinin nə olduğunu, necə tapıldığını və hansı praktiki əhəmiyyət kəsb etdiyini bilmək olduqca faydalıdır. Funksiyanın böhran nöqtəsi yalnız akademik deyil, gündəlik həyatda rast gəlinən bir çox texniki və iqtisadi problemlərin də effektiv həllində əsas vasitədir. Müxtəlif sahələrdə funksiyaların böhran nöqtələrinin analizi nəticələrin dəqiqliyini və etibarlılığını artırır, riskləri və itkiləri minimuma endirməyə kömək edir. Bu anlayış müasir riyaziyyatın və texnologiyanın inkişafında mühüm rol oynayır. Funksiyaların davranışının dərindən öyrənilməsi, onların böhran nöqtələrinin vaxtında və düzgün təyin olunması cəmiyyətin elmi və texnoloji səviyyəsinin inkişafına da öz töhfəsini verir.
Ən Çox Verilən Suallar
Funksiyanın böhran nöqtəsi dəyişənin müəyyən bir qiymətində funksiyanın davranışında əsaslı dəyişiklik baş verən nöqtədir. Bu nöqtədə funksiyanın törəməsi sıfıra bərabər olur və ya ümumiyyətlə mövcud olmur. Böhran nöqtəsində funksiya ya maksimum, ya minimum, ya da infleksiya yaşayır və bu, qrafikdə kəskin dönüş və ya əyriliyin dəyişməsi ilə nəzərə çarpır.
Böhran nöqtəsini tapmaq üçün əvvəlcə funksiyanın törəməsi alınır və sıfıra bərabər tutulur. Eyni zamanda törəmənin mövcud olmadığı nöqtələr də nəzərə alınır. Daha sonra ikinci törəmə yoxlanılır və bu nöqtənin ekstremum (maksimum/minimum) və ya infleksiya nöqtəsi olub-olmadığı müəyyən edilir.
Lokal maksimum, funksiyanın yaxın ətrafda aldığı ən böyük qiymətdir. Lokal minimum isə, yaxın ətrafda funksiyanın aldığı ən kiçik qiymətdir. Hər iki halda funksiyanın törəməsi sıfıra bərabər olur, lakin ikinci törəmə maksimumda mənfi, minimumda isə müsbət olur.
İnfleksiya nöqtəsi funksiyanın qrafikində əyriliyin istiqamətinin dəyişdiyi nöqtədir. Bu nöqtədə ikinci törəmə sıfıra bərabər olur, amma üçüncü törəmə sıfırdan fərqli olmalıdır. İnfleksiya nöqtəsində funksiya artmaqda və ya azalmaqda davam edə bilər, lakin əyrilik dəyişir.
Xeyr, bütün böhran nöqtələri ekstremum deyil. Ekstremumlar yalnız maksimum və minimum nöqtələridir. İnflexsiya nöqtələri də böhran nöqtəsi hesab olunsa da, burada funksiya maksimum və ya minimum almır, sadəcə əyrilik dəyişir.
Bəli, böhran nöqtələri gündəlik həyatda, xüsusilə iqtisadiyyat, mühəndislik, statistika və digər sahələrdə tez-tez tətbiq olunur. Məsələn, maksimum gəlir və ya minimal xərclə bağlı optimallaşdırma məsələlərində, proseslərin idarə olunmasında və risklərin qiymətləndirilməsində böhran nöqtələri əsas göstəricidir.
Bir funksiyada böhran nöqtələrinin sayı həmin funksiyanın tipindən və dərəcəsindən asılıdır. Bəzi sadə funksiyalarda bir və ya bir neçə böhran nöqtəsi ola bilər, mürəkkəb və çoxsahəli funksiyalarda isə onların sayı daha çox ola bilər. Hər bir böhran nöqtəsi funksiyanın davranışında əsaslı dəyişiklik yaradır.
Bəzən funksiyanın törəməsi analitik şəkildə tapılması çətin və ya mümkün olmur. Eyni zamanda törəmənin olmadığı nöqtələrin təyini və düzgün təsnifatı əlavə analiz və qrafik üsullar tələb edir. Mürəkkəb funksiyalarda isə köməkçi alqoritmlər və kompüter proqramları istifadə olunur.
İkinci törəmə, böhran nöqtəsinin maksimum, minimum və ya infleksiya nöqtəsi olmasını müəyyən etmək üçün əsas göstəricidir. Əgər ikinci törəmə mənfidirsə, maksimum, müsbətdirsə, minimum nöqtəsi sayılır. İkinci törəmə sıfırdırsa və üçüncü törəmə sıfırdan fərqli olarsa, bu infleksiya nöqtəsidir.
Böhran nöqtələri iqtisadi modelləşdirmə, maliyyə analitikası, mühəndislik sistemlərinin optimallaşdırılması, statistika, süni intellekt və təbiət elmləri daxil olmaqla bir çox sahədə geniş istifadə olunur. Bu nöqtələrin düzgün təyini və təhlili, qərarların dəqiqliyini artırır və optimallaşdırma imkanları yaradır.