Bərabəryanlı Trapesiyanın Sahəsi: Ümumi Tərif, Hesablanma Düsturu

Həndəsənin müxtəlif fiqurlarının öyrənilməsi riyaziyyatın əsas istiqamətlərindən biri kimi həm nəzəri, həm də praktik baxımdan böyük əhəmiyyət daşıyır. Bu fiqurlar içərisində trapesiya, xüsusən də bərabəryanlı trapesiya öz simmetriyası, estetik gözəlliyi və praktiki tətbiqləri ilə seçilir. Müasir dövrdə bərabəryanlı trapesiya yalnız riyazi araşdırmalarda deyil, memarlıqda, mühəndislikdə, texnologiyada və gündəlik həyatda da istifadə olunur. Onun sahəsinin düzgün hesablanması elmi-tədris fəaliyyətində, müxtəlif layihələrdə və hətta tikinti işlərində mühüm rol oynayır.

Bərabəryanlı trapesiya nədir? Əsas xüsusiyyətləri

Trapesiya – iki tərəfi paralel olan dördbucaqlıdır. Bərabəryanlı trapesiya (bəzən izoskel trapesiya da adlanır) isə həm də yan tərəfləri bir-birinə bərabər olan xüsusi trapesiya növüdür. Trapeyanın iki paralel tərəfi əsaslar adlanır, digər iki bərabər uzunluqlu tərəfi isə yanlar adlanır.
Bərabəryanlı trapesiya bu xüsusiyyətləri ilə fərqlənir:

• Yan tərəfləri (qolları) eyni uzunluqdadır.
• Əks bucaqlar bərabərdir.
• Onun daxilinə və xaricinə çevrə çəkmək mümkündür (müəyyən şərtlərlə).
• Simmetriya oxu var və bu ox əsasların orta nöqtəsindən keçir.
• Diagonal (köndələn) xətləri bərabər uzunluqlu olur.

Bu simmetrik və harmonik quruluş bərabəryanlı trapesiyanı müxtəlif sahələrdə daha geniş tətbiq olunan fiqura çevirir.

Bərabəryanlı trapesiya: Tarixi və nəzəri əhəmiyyəti

Trapesiya fiqurunun tarixi qədim Yunan riyaziyyatına gedib çıxır. O dövrdə alimlər dördbucaqlılar arasında fərqlilikləri araşdırıb, hər birinin sahə düsturunu və əsas xüsusiyyətlərini müəyyən ediblər. Bərabəryanlı trapesiya isə simmetrik fiqur kimi xüsusilə öyrənilib, çünki bu fiqurun daxili, bucaq və uzunluq bərabərlikləri nəzəri baxımdan olduqca maraqlıdır. Orta əsr ərəb və Avropa riyaziyyatında trapesiya – xüsusən də bərabəryanlı növü – müxtəlif memarlıq və mühəndislik layihələrinin layihələndirilməsində əsas element sayılırdı.

Bərabəryanlı trapesiya və gündəlik həyat

Bərabəryanlı trapesiya yalnız abstrakt riyazi fiqur deyil, gündəlik həyatda tez-tez rast gəlinən formadır. Körpülərdə, pilləkənlərdə, dam örtüklərində, bəzək elementlərində, hətta mebel dizaynında bu fiqurdan istifadə olunur. Memarlar və mühəndislər bu formadan tez-tez istifadə edirlər, çünki bərabəryanlı trapesiya həm möhkəm, həm də estetik cəhətdən cəlbedicidir. Onun sahəsinin düzgün hesablanması isə material sərfi, güc hesablamaları və planlaşdırma üçün əsas şərtdir.

Bərabəryanlı trapesiya sahəsinin əsas hesablanma düsturu

Bərabəryanlı trapesiyanın sahəsini tapmaq üçün aşağıdakı düsturdan istifadə edilir:

S = [(a + b) × h] / 2

Burada:

• S – trapesiyanın sahəsi,
• a və b – paralel əsasların uzunluqları,
• h – trapesiyanın hündürlüyü.

Bu düstur yalnız bərabəryanlı deyil, istənilən trapesiya üçün keçərlidir. Lakin bərabəryanlı trapesiyada hündürlüyün və yan tərəflərin əlavə düsturlarla tapılması prosesi daha asan olur.

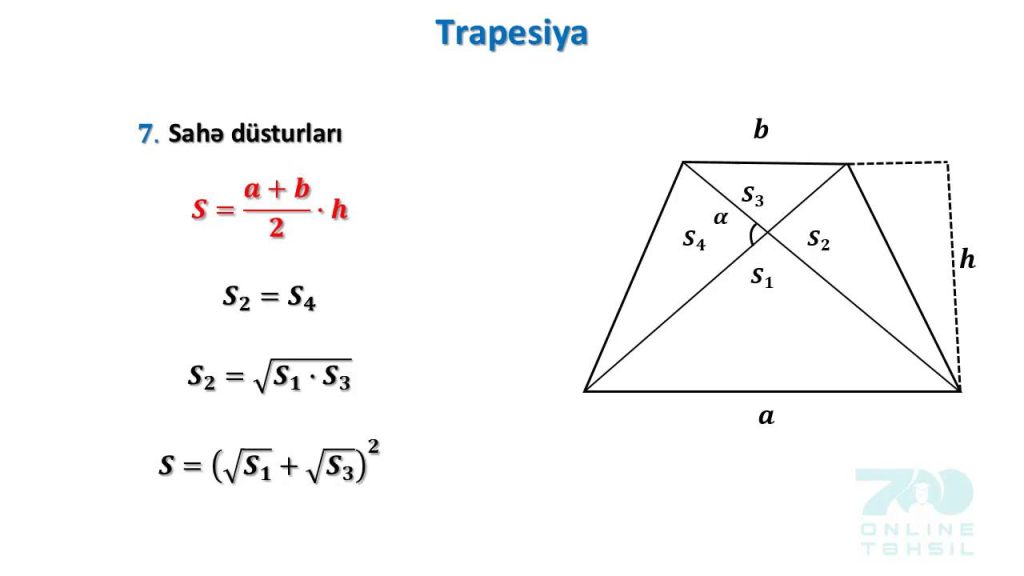
Yan tərəflər və hündürlük düsturu

Əgər əsasların uzunluğu (a, b) və yan tərəfin uzunluğu (c) məlumdursa, hündürlüyü aşağıdakı kimi hesablamaq olar:

h = √[c² – ((a-b)²/4)]

Bu düstur bərabəryanlı trapesiyanın əlavə imkanlarını açır və hər bir elementin hesablanmasında riyazi çevikliyi təmin edir.

Bərabəryanlı trapesiya: Digər riyazi xüsusiyyətlər

Bərabəryanlı trapesiyanın digər mühüm riyazi xüsusiyyətləri də var:

• Daxili bucaqları: Paralel əsasların yanında olan bucaqlar bir-birinə bərabər olur.
• Diagonallar (köndələn xətlər): Hər iki diagonal bərabərdir və onların uzunluğunu hesablamaq üçün kosinus teoremi və ya digər üsullar istifadə olunur.
• Orta xətt: Trapeyanın əsaslarının ortalarını birləşdirən düz xətt “orta xətt” adlanır və uzunluğu (a + b) / 2-dir.

Sahə düsturunun çıxarılması və izahı

Trapesiya sahəsi düsturu, əslində, paralel əsaslar və onların arasında olan hündürlük vasitəsilə iki üçbucağın və ya bir paralelqramın sahəsinə əsaslanır.

• Paralel əsaslar üst-üstə qoyulduqda, sanki iki bərabərtərəfli üçbucaq və bir ortaq düz bucaq düzəldir.
• Hündürlük əsasların arasındakı məsafədir.
• Bu düstur trapesiya sahəsinin tez və dəqiq tapılmasına imkan verir.

Praktik nümunələr və gündəlik tətbiqlər

Misal 1:
Bir bağ sahəsi bərabəryanlı trapesiya formasındadır. Əsasların uzunluğu 12 m və 8 m, yan tərəfləri isə 5 m-dir. Sahəni tapmaq üçün əvvəlcə hündürlüyü hesablayırıq:

h = √[5² – ((12-8)²/4)] = √[25 – (16/4)] = √[25 – 4] = √21 ≈ 4.58 m
S = [(12 + 8) × 4.58] / 2 = (20 × 4.58) / 2 = 91.6 / 2 = 45.8 m²

Bu tip hesablamalar tikinti, torpaq planlaşdırılması və müxtəlif sahələrdə tez-tez istifadə olunur.

Misal 2:
Əgər yalnız sahə və əsaslar məlumdur, yan tərəfləri tapmaq və ya digər elementləri hesablamaq üçün müxtəlif tərs düsturlardan istifadə olunur.

Bərabəryanlı trapesiya və digər dördbucaqlılarla müqayisə

Trapesiya xüsusiyyətlərinə görə paralelograma, düzbucaqlıya, kvadrata yaxın olsa da, əsas fərq yalnız iki tərəfinin paralel olması və yan tərəflərin bərabərliyidir. Bu quruluş onu həm estetik, həm də praktiki baxımdan universal edir. Dördbucaqlıların sahəsinin tapılmasında bərabəryanlı trapesiyanın rolu məktəb proqramlarında və elmi layihələrdə geniş şəkildə öyrədilir.

Bərabəryanlı trapesiyanın tarixi və mədəni simvolizmi

Bərabəryanlı trapesiya antik dövrdə tikililərdə, məbədlərdə və bədii naxışlarda geniş istifadə olunub. Bu fiqurun simmetriyası və sadə forması insanlarda tarazlıq, harmoniya və möhkəmlik hissi yaradır. Müasir memarlıqda isə bərabəryanlı trapesiya fasadlarda, körpülərdə, konstruksiya elementlərində tez-tez görünür.

Riyaziyyat və məktəb proqramlarında bərabəryanlı trapesiya

Azərbaycan məktəblərinin VI-VIII sinif riyaziyyat proqramlarında bərabəryanlı trapesiyanın sahəsinin hesablanması əsas mövzulardan biridir. Şagirdlər müxtəlif tapşırıqlarda bu düsturu tətbiq etməklə məntiqi təfəkkür, ölçmə və hesablama bacarıqlarını inkişaf etdirirlər. Testlərdə, olimpiadalarda və günlük həyatda bu biliklər daim lazım olur.

Bərabəryanlı trapesiyanın sahəsinin tərs məsələləri

Bəzən sahə məlum olur, əsas və ya yan tərəflər tapılmalıdır. Düsturları tərsinə qurmaq, müxtəlif riyazi manipulyasiyalar aparmaq tələb olunur. Bu, təcrübə və riyazi biliklərin möhkəmlənməsi üçün ideal fürsətdir.

Sahənin hesablama üsullarının üstünlükləri

Bərabəryanlı trapesiyanın sahəsi düsturunun əsas üstünlüyü onun sadəliyi, praktikliyi və universallığıdır. Əgər paralel əsaslar və hündürlük məlumdursa, sadəcə toplama, vurma və bölmə əməliyyatı ilə bir neçə saniyəyə istənilən nəticə əldə etmək olar. Bu isə vaxt və resurslara qənaət deməkdir.

Bərabəryanlı trapesiya riyaziyyatın, həndəsənin və gündəlik həyatın ən praktik, simmetrik və asan tətbiq olunan fiqurlarından biridir. Onun sahəsinin hesablanması həm məktəb yaşında, həm də peşəkar fəaliyyət göstərən şəxslər üçün vacib riyazi bacarıqdır. Bu biliklər memarlıqda, mühəndislikdə, təbiətşünaslıqda və gündəlik məişətdə istifadə olunur. Riyazi düsturların tətbiqi sayəsində hər kəs bərabəryanlı trapesiyanın istənilən elementini rahatlıqla hesablaya bilər. Bu isə praktiki həyatda düzgün planlaşdırma, düzgün material seçimi və dəqiq nəticə deməkdir.

Ən Çox Verilən Suallar