Riyaziyyatda çevrə anlayışı gündəlik həyatımızdan tutmuş, mühəndislik və elm sahələrinə qədər bir çox sahədə istifadə olunan əsas həndəsi fiqurlardan biridir. Çevrənin əsas xarakterik göstəricilərindən biri onun radiusudur. Radius çevrənin mərkəzindən onun üzərində yerləşən istənilən nöqtəyə qədər olan məsafədir. Bu sadə və anlaşıqlı tərif, əslində həndəsədə bir çox mürəkkəb və maraqlı problemlərin açarını təşkil edir. Çevrənin radiusu, həmçinin onun uzunluğunun, sahəsinin və digər həndəsi elementlərinin hesablanmasında əsas rol oynayır.
Radiusun düzgün başa düşülməsi və tətbiqi təkcə məktəb riyaziyyatı üçün deyil, həm də daha yüksək səviyyəli texniki və praktiki məsələlər üçün vacibdir. Məsələn, mühəndislikdə, memarlıqda, dizaynda və gündəlik məişətdə tez-tez çevrə və onun radiusu ilə bağlı hesablara rast gəlirik. Çevrə ilə bağlı aparılan istənilən ölçmə və ya layihələndirmə işində radiusdan istifadə etmək mütləqdir. Radius həndəsi bərabərliklərin və simmetriyanın əsasını təşkil edir.
Hər bir şagird və ya tələbə üçün radiusun nə demək olduğunu, onu necə tapmaq və harada tətbiq etmək mümkünlüyünü bilmək vacib bacarıqlardan biridir. Çevrə radiusunun xüsusiyyətlərini başa düşmək, daha mürəkkəb fiqurların – dairənin, silindrin, kürənin və hətta real həyatda rast gəlinən bir çox obyektlərin ölçülərinin hesablanmasında əsas rol oynayır. Radiusun müxtəlif üsullarla tapılması və onun əyani şəkildə izahı, həndəsə dərslərinin ən maraqlı və fundamental hissələrindən sayılır.
Çevrənin radiusu, onun diametri, çevrəsi və sahəsi arasında sıx əlaqə yaradır. Bu anlayışlar bir-biri ilə qarşılıqlı əlaqədə olmaqla, riyaziyyatın əsas həndəsi qanunauyğunluqlarını üzə çıxarır. Radius həm də təbiətdə, texnikada və sənətdə simmetriya və balansın əsas elementlərindən biridir. Bu baxımdan, radiusun əhəmiyyəti təkcə riyazi formal qaydalarla deyil, həm də vizual və funksional baxımdan böyükdür.
Radiusun Həndəsi Tərifi və Əsas Xüsusiyyətləri
Çevrənin radiusu mərkəz nöqtədən çevrə üzərindəki istənilən nöqtəyə çəkilmiş düz xətt parçasıdır. Radius riyazi olaraq r hərfi ilə işarə edilir və onun uzunluğu çevrənin hər bir hissəsində eynidir. Bu xüsusiyyət çevrənin bərabər məsafəli olması, yəni tam simmetrik həndəsi fiqur kimi formalaşmasının əsas səbəbidir.
Çevrədə istənilən nöqtə radiusun uzunluğuna bərabər məsafədə yerləşir. Bu prinsip, çevrənin sahəsinin, diametrinin və digər həndəsi elementlərinin hesablama qaydalarının da əsasını təşkil edir. Radiusun dəqiq müəyyən olunması, digər həndəsi elementlərin hesablama dəqiqliyinə də birbaşa təsir edir.
Çevrənin Radiusu və Diametri Arasındakı Münasibət
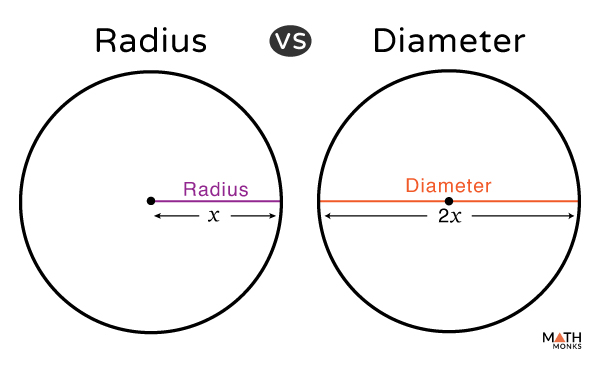
Radius və diametr çevrənin iki əsas ölçü göstəricisidir. Diametr – çevrənin mərkəzindən keçən və onun iki nöqtəsini birləşdirən ən uzun xəttdir. Diametr həmişə radiusun iki misli olur, yəni d = 2r. Bu sadə formula radiusun tapılması və ya diametrdən radiusa keçid üçün əsas alət hesab olunur.
Çox zaman praktiki məsələlərdə çevrənin diametri verilir və radiusun tapılması tələb olunur. Əgər diametr məlumdursa, onu iki hissəyə bölməklə radius əldə edilir. Əksinə, radius məlum olduqda, onu iki dəfə artırmaqla diametr tapılır.
Çevrənin Radiusunun Tapılması Yolları
Radiusun tapılması üçün bir neçə əsas üsul var. Ən sadə üsul diametrin məlum olmasıdır – diametrin yarısı radiusu verir. İkinci yol çevrənin uzunluğunun (C) məlum olmasıdır. Çevrənin uzunluğu C = 2πr düsturuna əsaslanır və buradan radius r = C / (2π) şəklində tapılır.
Üçüncü əsas üsul çevrənin sahəsinin (S) məlum olmasıdır. Çevrənin sahəsi S = πr² kimi hesablanır və radius r = √(S/π)düsturu ilə tapılır. Bu metodlar məktəb həndəsəsində və gündəlik həyatdakı tətbiqlərdə ən çox istifadə olunan hesablama yollarıdır.
Çevrənin Radiusu və Onun Tətbiq Sahələri
Radius anlayışı yalnız nəzəri həndəsə ilə məhdudlaşmır. Mühəndislik, memarlıq, nəqliyyat, aviasiya, dizayn və bir çox digər sahələrdə çevrə radiusunun ölçülməsi və hesablanması zəruridir. Məsələn, avtomobil təkərlərinin, saatların, su borularının, tankların və s. radiusu düzgün hesablanmazsa, texniki problemlər yarana bilər.
Radiusun düzgün seçilməsi obyektin dayanıqlığına, funksionallığına və estetik görünüşünə birbaşa təsir edir. Buna görə də, radiusun düzgün hesablanması və tətbiqi real həyatda mühüm əhəmiyyət daşıyır.
Çevrənin Radiusunun Riyazi Düsturlarla İfadəsi
Çevrənin radiusu bir neçə əsas riyazi düsturla ifadə olunur. Əgər diametr d məlumdursa: r = d / 2. Çevrənin uzunluğu Cverilibsə: r = C / (2π). Əgər sahə S məlumdursa: r = √(S/π). Hər bir düstur konkret praktiki və ya nəzəri vəziyyətdə tətbiq edilir və radiusun tapılmasını asanlaşdırır.
Bu düsturlar təkcə çevrənin deyil, həm də daha mürəkkəb fiqurların və real obyektlərin ölçülməsində əsas rol oynayır. Düsturların düzgün tətbiqi nəticənin dəqiqliyini təmin edir və həndəsi məsələlərin həllini sürətləndirir.
Radiusun Təbiətdə və Texnikada Rolu
Təbiətdə çoxlu sayda obyektin və canlıların quruluşunda çevrənin radiusu önəmli yer tutur. Məsələn, meyvələrin, çiçəklərin, ağacların kəsiklərinin və s. radiusu onların quruluşunu və həyat fəaliyyətini müəyyənləşdirir. Texnikada isə radiusun düzgün hesablanması müxtəlif cihaz və avadanlıqların işləkliyinə və davamlılığına birbaşa təsir edir.
Bir çox texnoloji cihaz və konstruksiyalar üçün optimal radiusun seçilməsi onların səmərəliliyi və təhlükəsizliyi baxımından vacibdir. Bu səbəbdən, radius anlayışı həm elmi, həm də gündəlik məişət səviyyəsində böyük aktuallıq kəsb edir.
Çevrənin Radiusunun Ölçülməsi və Dəqiqliyi
Radiusun düzgün ölçülməsi üçün müxtəlif ölçü cihazlarından və texnikalardan istifadə edilir. Sadə hallarda xətt ölçən (çəkic), cetvel və ya kompasdan istifadə olunur. Daha mürəkkəb hallarda isə lazer ölçü cihazları və digər dəqiq alətlər tətbiq olunur.
Dəqiq ölçmələr həm tədris, həm də peşəkar səviyyədə əhəmiyyətlidir. Dəqiqlik yüksək olduqda, radiusa əsaslanan digər hesabat və ölçülərin də səhvsiz olması təmin olunur.
Çevrənin Radiusu ilə Bağlı Tipik Məsələlər və Nümunələr
Məktəb proqramlarında və gündəlik həyatda radiusun tapılması ilə bağlı bir çox tipik məsələ mövcuddur. Məsələn, diametri 10 sm olan çevrənin radiusu 5 sm-dir. Çevrənin uzunluğu 31,4 sm-dirsə, radius 5 sm olur. Sahəsi 78,5 sm² olan çevrənin radiusu isə 5 sm-dir.
Bu tip məsələlər radius anlayışını möhkəmləndirir və şagirdlərin, tələbələrin həndəsi bacarıqlarını inkişaf etdirir. Hər bir riyazi məsələ radiusun daha yaxşı qavranılması və tətbiqi üçün mühüm rol oynayır.
Cədvəl: Radiusun Tapılması Yolları və Düsturları
| Verilən | Düstur | Radiusun Tapılması |
|---|---|---|
| Diametr (d) | r = d / 2 | d-ni 2-yə bölürük |
| Çevrənin uzunluğu (C) | r = C / (2π) | C-ni 2π-ə bölürük |
| Sahə (S) | r = √(S/π) | S-ni π-ə bölüb kök altına salırıq |
| Koordinatlarla (x, y) | r = √((x-a)²+(y-b)²) | Mərkəzdən nöqtəyə məsafə hesablanır |
Çevrənin radiusu həndəsənin və ümumilikdə riyaziyyatın ən fundamental anlayışlarından biridir. Bu ölçü vahidi müxtəlif sahələrdə, o cümlədən elm, texnika, memarlıq və gündəlik məişətdə geniş tətbiq edilir. Radiusun başa düşülməsi və düzgün tətbiqi, çevrənin və daha mürəkkəb həndəsi fiqurların öyrənilməsində əsas rol oynayır. Hər bir şagird, tələbə və ya mütəxəssis üçün radiusun tərifi, hesablama qaydaları və tətbiq sahələri haqqında biliklər gündəlik işlərin və elmi layihələrin uğurla həyata keçirilməsi üçün zəruridir.
Radius yalnız riyazi deyil, eyni zamanda təbiətdə və insan fəaliyyətində simmetriya, harmoniya və balansın təcəssümüdür. Düzgün seçilmiş və tətbiq olunmuş radius həm obyektin funksionallığını, həm də estetik görünüşünü təmin edir. Çevrə ilə bağlı riyazi məsələlərdə radiusun dəqiq hesablanması ümumi həndəsi təfəkkürün və analitik bacarıqların inkişafında əsas amildir. Radiusun əhəmiyyətinin və tətbiqinin dərk edilməsi, riyazi savadlılıq və mühəndislik düşüncəsinin formalaşmasında mühüm rol oynayır.
Ən Çox Verilən Suallar
Çevrənin radiusu mərkəzdən çevrə üzərindəki istənilən nöqtəyə qədər olan məsafədir. Bu, çevrənin ən əsas həndəsi göstəricilərindən biridir. Radius bərabər məsafəli olduğuna görə çevrə ideal simmetrik fiqurdur. Riyaziyyatda radius adətən r hərfi ilə işarə edilir.
Çevrənin radiusunu tapmaq üçün bir neçə əsas üsul mövcuddur: diametrin yarısı, çevrənin uzunluğunun 2π-ə bölünməsi və sahənin π-ə bölünüb kök altına salınması. Hər bir üsul konkret praktiki vəziyyət üçün istifadə olunur. Verilənlərdən asılı olaraq uyğun düstur seçilir.
Diametr çevrənin mərkəzindən keçən ən uzun xəttdir və həmişə radiusun iki misli olur. Riyazi olaraq d = 2r şəklində yazılır. Bu, radiusun diametrə görə, və ya əksinə, asanlıqla tapılmasını təmin edir.
Çevrənin radiusu müxtəlif sahələrdə – memarlıqda, mühəndislikdə, dizaynda, mexanikada və gündəlik məişətdə istifadə olunur. Məsələn, təkərlərin, saatların, müxtəlif mexanizmlərin və hətta su borularının ölçülərində radius əsas göstəricidir. Radiusun düzgün seçilməsi obyektin işləkliyinə birbaşa təsir edir.
Çevrənin sahəsi S = πr² düsturu ilə hesablanır. Burada r radius, π isə təxminən 3,14-dir. Radius məlum olduqda, onu kvadrata yüksəldib π-ə vurmaq lazımdır. Bu, çevrənin daxilindəki bütün nöqtələrin sahəsinin ölçülməsi deməkdir.
Sadə hallarda çəkic, cetvel, kompas və digər həndəsi ölçü alətlərindən istifadə edilir. Daha mürəkkəb ölçmələrdə lazer cihazları və xüsusi həndəsi ölçü texnikaları tətbiq olunur. Seçilən üsulun dəqiqliyi radiusun düzgün təyinində əsas rol oynayır.
Çevrənin uzunluğu C = 2πr düsturuna əsaslanır. Əgər çevrənin uzunluğu məlumdursa, onu 2π-ə bölməklə radiusu tapmaq olar. Məsələn, C=31,4 sm-dirsə, radius r = 31,4 / (2×3,14) = 5 sm olur.
Təbiətdə radiusun rolu böyükdür. Çoxlu sayda canlı və cansız obyektin forması və quruluşunda radius əsas parametrdir. Meyvələrin, hüceyrələrin, su damcılarının və bir çox digər obyektlərin radiusu onların həyat fəaliyyətini və quruluşunu müəyyənləşdirir.
Texnikada radiusun düzgün hesablanması bir çox mexanizmin işləkliyi və dayanıqlığı üçün əsas şərtdir. Məsələn, avtomobil təkərləri, dişlilər, turbinalar və bir çox digər qurğular radiusa əsaslanır. Düzgün radius məhsulun keyfiyyəti və təhlükəsizliyi üçün vacibdir.
Məktəb proqramlarında ən çox diametri, sahəsi və ya çevrənin uzunluğu verilmiş çevrənin radiusunu tapmaq tələb olunur. Hər biri üçün fərqli düsturlar tətbiq edilir. Bu məsələlər şagirdlərin həndəsi və analitik bacarıqlarının inkişafına xidmət edir.