Riyaziyyat təbiətin dilidir və bu dilin əsas anlayışlarından biri də çevrə və onun sahəsidir. Hər gün rast gəldiyimiz dairəvi formalar, təkərlər, boşqablar, siferblatlar və hətta planetlərin orbitləri, çevrənin sadə, lakin əhəmiyyətli bir riyazi model olduğunu göstərir. Bu formanın sahəsinin necə hesablandığını bilmək, sadəcə məktəb təhsili üçün deyil, həm də real həyatda qarşımıza çıxan çoxsaylı məsələlərin həllində istifadə olunur. Çevrə anlayışı qədim dövrlərdən bəri öyrənilir. Antik yunan riyaziyyatçılarının araşdırmalarından tutmuş müasir tətbiqi elmlərə qədər, bu forma və onun sahəsi riyaziyyatın fundamental məsələlərindən biri olmuşdur. Çevrənin sahəsinin hesablanması üçün istifadə olunan formul sadə görünə bilər, lakin onun arxasında dayanan məntiq, konsepsiyalar və tətbiqlər olduqca zəngindir. Sahə dedikdə, bir səthin tutduğu ümumi ölçü nəzərdə tutulur və çevrənin sahəsi də həmin dairəvi bölgənin ölçüsünü ifadə edir. Bu sahə radiusla sıx bağlıdır və π (pi) sabitindən istifadə edilməklə müəyyən olunur. Bu sabitin tətbiqi çevrənin uzunluğu ilə sahəsi arasındakı əlaqəni dərinləşdirir və onu universal bir riyazi vasitəyə çevirir.
Çevrə nədir və əsas anlayışlar
Çevrə, eyni mərkəzdən bərabər məsafədə yerləşən bütün nöqtələrin birləşməsindən ibarət olan qapalı əyridir. Onun mərkəzi, radiusu və diametri bu həndəsi formanın əsas tərkib hissələridir. Radius, çevrənin mərkəzindən onun istənilən nöqtəsinə qədər olan məsafədir, diametr isə mərkəzdən keçən və çevrəni iki bərabər hissəyə bölən düz xəttdir.
Çevrənin sahəsi isə, bu əyrinin daxilində yerləşən bütün nöqtələrin yaratdığı ikiölçülü bölgənin ölçüsüdür. Bu sahə dairənin tamlığı ilə bağlı olduğu üçün sahənin hesablanması radiusdan və sabit π dəyərindən asılıdır. Beləliklə, çevrə sahəsi riyaziyyatın ən fundamental həndəsi anlayışlarından biri kimi çıxış edir və digər formaların sahələrinin hesablanması üçün baza təşkil edir.
Çevrənin sahəsinin formulu
Çevrənin sahəsini hesablamaq üçün ən çox istifadə olunan formul aşağıdakı kimidir: S = π × r². Bu formulda “S” sahəni, “r” isə radiusu ifadə edir. π isə təxminən 3.1416 olan sabit bir ədəddir və bütün çevrələr üçün universal sabit olaraq qəbul edilir.
Bu formulun sadəliyi onun praktikliyini artırır. Yəni istənilən radiusa sahib çevrənin sahəsini hesablamaq üçün sadəcə radiusu kvadrata yüksəldib π ilə vurmaq kifayətdir. Riyaziyyat dərslərində bu formuldan geniş istifadə olunur və müxtəlif nümunələrlə möhkəmləndirilir. Mühəndislikdə, dizaynda və hətta iqtisadi hesablamalarda belə çevrənin sahəsinin dəqiq hesablanması vacib rol oynayır.
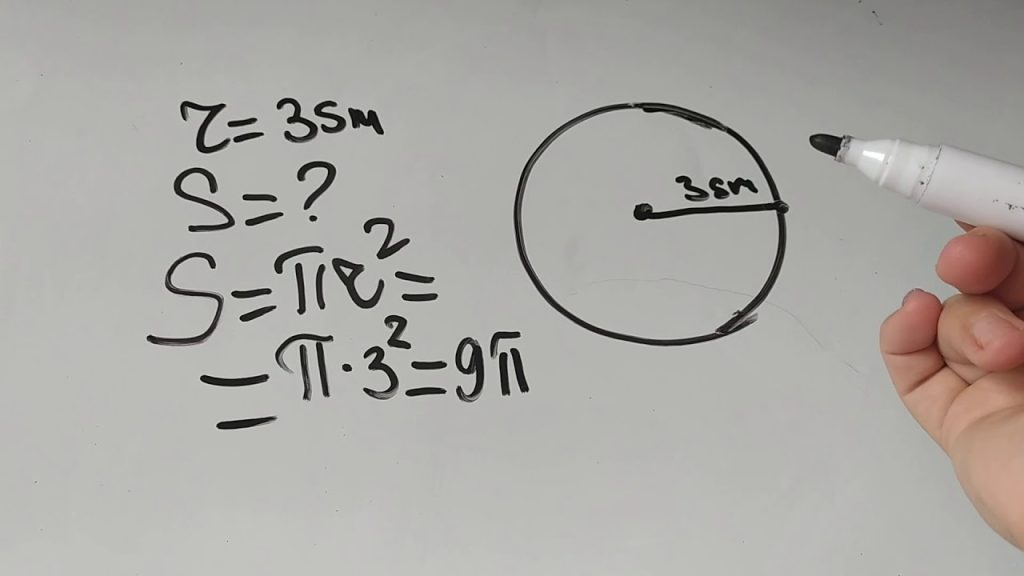
Radius və diametrin təsiri
Radius, çevrənin sahəsini təyin edən əsas parametrdir. Sahə radiusun kvadratına birbaşa bağlı olduğu üçün, radiusdakı kiçik dəyişiklik belə sahənin ölçüsündə böyük fərq yarada bilər. Məsələn, radius iki dəfə artırıldıqda, sahə dörd dəfə artır.
Eyni zamanda, diametr radiusun iki misli olduğuna görə, çevrənin sahəsini diametr vasitəsilə də hesablamaq mümkündür. Belə olduqda formul belə dəyişir: S = (π × d²)/4. Bu formul da radiuslu formul kimi effektiv və geniş tətbiq olunan üsuldur. Bu iki parametrin dəyişkənliyi sahənin ölçüsündə böyük fərqlər yaratdığından, düzgün ölçmə və hesablama vacibdir.
π (Pi) ədədinin rolu
π (pi) sabiti çevrənin sahəsinin hesablanmasında əvəzolunmazdır. O, çevrənin uzunluğunun onun diametrinə nisbətini ifadə edən sabitdir və riyaziyyatda və digər elmlərdə geniş istifadə olunur. Bu sabitin dəqiq dəyəri sonsuz onluq kəsr şəklindədir və tam olaraq ifadə olunmur, lakin praktik məqsədlər üçün 3.14 və ya 3.1416 kimi təxmini dəyərlərdən istifadə olunur.
Riyazi olaraq, π sabitinin əhəmiyyəti yalnız çevrə ilə məhdudlaşmır. O, inteqral hesablamalarda, dalğa nəzəriyyəsində, hətta statistika və fizika sahələrində də qarşımıza çıxır. Çevrənin sahəsinin hesablanması kontekstində isə π sabiti sahəni təyin edən əsas riyazi elementdir. Bu səbəbdən də, onun düzgün tətbiqi uğurlu hesablama üçün vacib şərtdir.
Real həyatda tətbiqlər
Çevrənin sahəsi anlayışı təkcə dərsliklərlə məhdudlaşmır. Bu bilik bir çox sahədə praktik şəkildə istifadə olunur. Məsələn, avtomobil təkərlərinin dizaynı, su anbarlarının həcmi, dairəvi ərazilərin ölçülməsi kimi məsələlərdə çevrənin sahəsi hesablanır.
Müasir texnologiyalarda, xüsusilə aerokosmik sənayedə, çevrənin sahəsi kimi hesablama üsulları cihazların effektiv dizaynında əhəmiyyətlidir. Eyni zamanda memarlıqda, idman meydançalarının planlaşdırılmasında və hətta kənd təsərrüfatında əkin sahələrinin bölünməsi kimi sahələrdə də bu bilikdən istifadə olunur. Beləliklə, bu riyazi anlayış həyatın müxtəlif sahələrində vacib rol oynayır.
Müxtəlif radiuslara görə sahə fərqləri
Çevrənin radiusu dəyişdikcə, sahədəki dəyişiklik kvadratik olaraq artır. Məsələn, radius 2 sm olduqda sahə təxminən 12.57 sm², 4 sm olduqda isə 50.26 sm² olur. Bu fərq radiusun kvadrata yüksəldilməsi və π ilə vurulmasından irəli gəlir. Aşağıdakı cədvəldə müxtəlif radiuslara görə sahələrin təxmini hesablanması təqdim olunub:
| Radius (r) | Sahə (S = π × r²) |
|---|---|
| 1 sm | 3.14 sm² |
| 2 sm | 12.57 sm² |
| 3 sm | 28.27 sm² |
| 4 sm | 50.26 sm² |
| 5 sm | 78.54 sm² |
Bu cədvəl radiusun cüzi artımının sahənin ciddi şəkildə böyüməsinə səbəb olduğunu göstərir. Bu, dizayn və mühəndislik işlərində də nəzərə alınmalıdır.
Hesablamalarda yol verilən səhvlər
Çevrənin sahəsini hesablamaq zamanı ən çox rast gəlinən səhvlərdən biri π dəyərinin düzgün istifadə edilməməsidir. Bəzən təxmini 3 əvəzinə 3.14 və ya 3.1416 kimi dəyərlərdən istifadə olunmaması nəticəsində hesablamalar dəqiq olmur. Digər bir səhv isə radius əvəzinə diametrin istifadə olunmasıdır.
Sahə formulunda radius əsas rol oynadığından, ölçmənin düzgün aparılması çox vacibdir. Eyni zamanda formulun kvadrat komponenti (r²) bəzən nəzərə alınmır və sadəcə π × r kimi hesablanır. Bu kimi yanlışlıqlar nəticəsində əldə olunan nəticə tamamilə səhv olur və texniki işlərdə ciddi fəsadlara yol aça bilər.
Çevrə sahəsinin digər formalarla müqayisəsi
Çevrənin sahəsi ilə kvadrat, düzbucaqlı və ya üçbucağın sahəsi arasında fərqlər əsasən formulların quruluşuna və təbiətinə bağlıdır. Məsələn, kvadratın sahəsi a² formuluna əsaslanır və sadə şəkildə tərəflərin vurulması ilə alınır. Dairədə isə radius kvadratlaşdırılır və π ilə vurulur. Bu səbəbdən dairənin sahəsi daha kompleks, lakin dəqiq modeldir.
Digər formalarla müqayisədə çevrənin sahəsi daha simmetrik və hər tərəfdən eyni məsafəli bölgəni ifadə etdiyi üçün bəzi mühəndislik və sənaye sahələrində daha çox üstünlük təşkil edir. Onun praktik quruluşu, riyazi modellərdə və fiziki tətbiqlərdə çevikliyi artırır.
Çevrənin sahəsinin hesablanması sadə görünsə də, riyazi və praktiki baxımdan böyük əhəmiyyətə malikdir. Bu anlayış təkcə məktəbdə öyrədilən bir formula ilə məhdudlaşmır, əksinə, real həyatda geniş tətbiqləri ilə riyaziyyatın canlı tərəfini əks etdirir. Radiusun və π sabitinin qarşılıqlı əlaqəsi sahənin dəqiq hesablanmasına imkan yaradır və bu da müasir texnologiyaların müxtəlif sahələrində uğurla tətbiq olunur.
Dairəvi formaların ölçülməsi memarlıqdan kosmosa qədər bir çox sahədə vacib rol oynayır. Onun düzgün hesablanması həm maddi, həm də funksional baxımdan optimallıq yaradır. Ən kiçik radius dəyişikliyi belə böyük sahə fərqlərinə səbəb ola bilir və bu, layihələndirmə və hesablamalarda nəzərə alınmalıdır.
Çevrənin sahəsi haqqında biliklər yalnız riyazi bacarığı artırmır, eyni zamanda məntiqi düşüncə və analitik yanaşmanı da inkişaf etdirir. Bu anlayışla tanış olanlar, digər həndəsi formaların da dəyərləndirilməsində daha peşəkar yanaşma nümayiş etdirə bilərlər.
Ən Çox Verilən Suallar
Çevrənin sahəsi, mərkəz nöqtəsi ətrafında yerləşən dairəvi bölgənin tutduğu ümumi sahəni ifadə edir. Bu sahə radiusa və π sabitinə bağlıdır. S = π × r² formulu ilə hesablanır. Riyazi və praktiki baxımdan geniş tətbiqlərə malikdir.
Çevrənin sahəsini hesablamaq üçün radius kvadrata yüksəldilir və π (pi) ilə vurulur. Yəni S = π × r². Radius düzgün ölçülməlidir və π sabiti təxmini 3.1416 qəbul edilir.
Əgər diametr məlumdursa, o zaman sahə belə hesablanır: S = (π × d²)/4. Bu zaman diametr kvadrata yüksəldilir və π ilə vurularaq dördə bölünür. Nəticə eyni dəyəri verir.
π sabiti riyaziyyatda sonsuz onluq kəsrdir. Ən geniş qəbul olunan təxmini dəyəri 3.1416-dır. Bəzi hesablamalarda 3.14 və ya 22/7 kimi də istifadə olunur.
Sahə radiusun kvadratına bağlı olduğu üçün radius artdıqca sahə sürətlə artır. Məsələn, radius iki dəfə artırılsa, sahə dörd dəfə artır. Bu, sahənin kvadrat funksiya olması ilə bağlıdır.
Çevrənin sahəsi memarlıq, mühəndislik, dizayn, kənd təsərrüfatı və texnologiyada geniş istifadə olunur. Həmçinin su anbarlarının həcmi və dairəvi ərazilərin planlamasında da tətbiq edilir.
Ən çox rast gəlinən səhvlər π dəyərinin yanlış seçilməsi, radiusun əvəzinə diametrin istifadə olunması və r² əvəzinə sadəcə r-in götürülməsidir. Bu cür səhvlər nəticənin yanlış çıxmasına səbəb olur.
Kvadratın sahəsi bir tərəfin kvadratına bərabərdir: S = a². Çevrənin sahəsində isə radius və π sabiti istifadə olunur. Dairə daha simmetrik və mərkəzə bərabər məsafədə olan nöqtələrdən ibarətdir.
Kalkulyator dəqiqlik üçün faydalıdır, xüsusilə π sabitinin dəqiq dəyəri ilə hesablamalar üçün. Ancaq sadə təxmini dəyərlərlə əllə də hesablamaq mümkündür.
Azərbaycan təhsil proqramına əsasən, çevrənin sahəsi adətən VI və ya VII sinifdə həndəsə bölməsində tədris olunur. Bu mövzu riyazi düşüncənin inkişafında mühüm rol oynayır.