Dördbucaqlı, riyaziyyatın və həndəsənin ən fundamental fiqurlarından biri kimi həm təhsil, həm elmi tədqiqat, həm də gündəlik həyatda əhəmiyyətli rol oynayır. Bu fiqur yalnız nəzəri həndəsənin əsasını təşkil etmir, həmçinin memarlıqda, dizaynda, sənayedə və təbiətdə saysız-hesabsız tətbiq və nümunələrlə qarşılaşırıq. Dördbucaqlı bəsit görünüşünə baxmayaraq, onun quruluşunda, xüsusiyyətlərində və növlərində çoxsaylı məqamlar və incəliklər gizlənir. Hər bir dördbucaqlı həm simmetriya, həm də variasiya baxımından unikal və maraqlı xüsusiyyətlər daşıyır. Bu məqalədə dördbucaqlının dəqiq riyazi tərifi, növləri, əsas xüsusiyyətləri, sahə və perimetrin hesablanması, təbiətdə və insan fəaliyyətində tətbiqi, tarixi və simvolik mənası, həmçinin gündəlik həyatda rast gəldiyimiz müxtəlif formalı dördbucaqlıların praktiki əhəmiyyəti hərtərəfli və elmi əsaslarla təqdim olunur.
Dördbucaqlının riyazi tərifi və elementləri
Dördbucaqlı dörd tərəfi və dörd zirvəsi olan, bir düz müstəvidə yerləşən sadə həndəsi fiqurdur. Onun bütün tərəfləri kəsişməyən, dörd nöqtə (zirvə) və bu nöqtələri birləşdirən dörd düz xətt parçası ilə formalaşır. Dördbucaqlının əsas elementlərini aşağıdakı kimi təsnif etmək olar:
- Tərəflər: Dördbucaqlının dörd kənarı vardır.
- Zirvələr: Hər tərəfin birləşdiyi nöqtələrə zirvə deyilir. Dördbucaqlının dörd zirvəsi olur.
- Daxili bucaqlar: Dörd daxili bucaq, ümumi cəmi 360 dərəcə təşkil edir.
- Diagonallar: Zirvələri bir-biri ilə birləşdirən iki daxili xətt (diagonal) mövcuddur.
Dördbucaqlının növləri və xüsusiyyətləri onun tərəflərinin uzunluğu, bucaqların böyüklüyü və simmetriya vəziyyəti ilə müəyyən edilir.
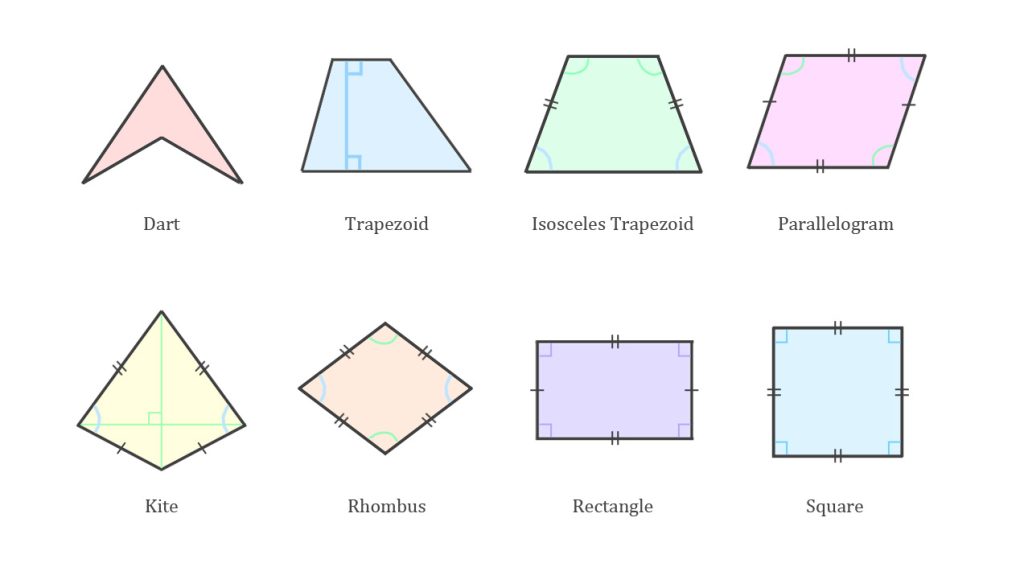
Dördbucaqlıların əsas növləri
Dördbucaqlının bir neçə əsas növü vardır. Hər birinin özünəməxsus riyazi xüsusiyyətləri, sahə və perimetr düsturları, simmetriya və praktik tətbiqləri olur.
| Dördbucaqlı növü | Tərəf və bucaq xüsusiyyətləri | Simmetriya | Əlamətdar cəhətləri |
|---|---|---|---|
| Kvadrat | Bütün tərəflər və bucaqlar bərabər | Yüksək | Dörd bərabər tərəf və 90° bucaq |
| Düzbucaqlı | Qarşı tərəflər bərabər, bucaqlar 90° | Orta | İki cüt bərabər tərəf |
| Paralelogram | Qarşı tərəflər bərabər və paralel | Orta | Qarşı bucaqlar bərabərdir |
| Romboid | Qarşı tərəflər paralel, bərabər deyil | Zəif | Simmetriya az, bucaqlar fərqlidir |
| Romblar | Bütün tərəflər bərabər, qarşı tərəflər paralel | Yüksək | Diagonallar bir-birini kəsir |
| Trapesiya | Yalnız bir cüt qarşı tərəf paralel | Yox və ya zəif | Çox müxtəlif formalar |
| Bərabəryanlı trapesiya | Yan tərəflər bərabər | Simmetrik | Əlamətdar orta xətt |
Bu növlərin hər birinin fərqli tətbiq və riyazi xüsusiyyəti mövcuddur.
Dördbucaqlının sahə və perimetrinin hesablanması
Dördbucaqlının sahəsinin və perimetrinin hesablanması onun növündən və tərəflərinin ölçülərindən asılıdır. Ən sadə hallarda, məsələn, kvadrat və düzbucaqlıda:
- Kvadrat: Sahə S=a2S=a2, Perimetr P=4aP=4a
- Düzbucaqlı: Sahə S=a×bS=a×b, Perimetr P=2(a+b)P=2(a+b)
- Paralelogram: Sahə S=a×hS=a×h, burada hh – uyğun tərəfə endirilən hündürlükdür.
- Trapesiya: Sahə S=(a+b)×h2S=2(a+b)×h, burada aa və bb paralel tərəflər, hh isə onların arasındakı hündürlükdür.
Dördbucaqlıların ümumi halda sahəsini hesablayarkən bir neçə üsul və düsturdan istifadə olunur, bəzi hallarda isə onu üçbucaqlara bölərək sahə hesablanır.
Dördbucaqlının simmetriya və məkan xüsusiyyətləri
Dördbucaqlının simmetriya xüsusiyyətləri onun növündən asılı olaraq dəyişir. Kvadrat və rombda dörd simmetriya oxu və yüksək simmetriya müşahidə olunur. Düzbucaqlı və paralelogramda isə yalnız iki simmetriya oxu olur. Trapesiya və digər qeyri-müntəzəm dördbucaqlılarda simmetriya az və ya heç olmur.
Diagonalların uzunluğu və kəsişmə nöqtəsi də dördbucaqlının növünü müəyyənləşdirir. Kvadratda və düzbucaqlıda diagonallar bir-birinə bərabərdir, paralelogramda isə kəsişmə nöqtəsində bərabər uzunluqlu hissələrə bölünmür.
Dördbucaqlının tarixi və mədəni mənası
Dördbucaqlı həndəsənin yaranma tarixində və riyaziyyatın inkişafında mühüm mərhələ hesab olunur. Qədim Misirdə, Babilistanda, Hindistanda dördbucaqlı torpaq sahələrinin ölçülməsi, binaların planlaşdırılması və abidələrin qurulmasında əsas ölçü vahidi kimi istifadə olunub. Dördbucaqlı həm də sabitlik, təhlükəsizlik və mükəmməllik simvoludur. Müasir dünyada kvadrat və düzbucaqlı şəhərsalmanın, inşaatın və memarlığın əsas konstruksiyası kimi tanınır.
Dördbucaqlıların gündəlik həyatda tətbiqi
Dördbucaqlı formalar gündəlik həyatda və insan fəaliyyətində ən çox rast gəlinən həndəsi fiqurlardandır. Binaların və otaqların planı, pəncərə və qapıların forması, yol nişanları, kitab və dəftər səhifələri, mebel əşyaları, hətta mobil telefon və ekranlar – bunların hamısı dördbucaqlı və onun alt növlərinin müxtəlif nümunələridir.
İnşaat və dizayn sahəsində dördbucaqlı fiqurlar istər gücün bərabər paylanmasında, istər estetik gözəllikdə, istərsə də material qənaətində müstəsna rol oynayır. Hətta elmi cədvəllər və qrafiklər də əsasən dördbucaqlı sahələrə bölünür.
Dördbucaqlının təbiətdə və texnologiyada nümunələri
Təbiətdə bir çox kristal və mineralların forması dördbucaqlıya yaxındır. Bitki yarpaqlarının, bəzi həşəratların qanadlarının və bəzi heyvanların bədən hissələrinin forması dördbucaqlının variasiyalarını xatırladır. Texnologiyada isə dördbucaqlı forması praktiki üstünlüklərə görə geniş istifadə olunur: monitorlar, televizorlar, taxta və metal lövhələr, konteynerlər, tikinti blokları və s.
Dördbucaqlının riyazi və praktiki əhəmiyyəti
Dördbucaqlıların tədqiqi, onların xüsusiyyətləri, sahə və perimetrinin hesablanması, koordinat sistemində təsviri və digər riyazi məsələlərin həlli şagirdlərin və tələbələrin məntiqi təfəkkürünün inkişafında mühüm rol oynayır. Praktiki baxımdan isə, torpaq sahəsinin ölçülməsi, planlaşdırılması, dizayn, tikinti və digər sahələrdə dəqiq hesabat aparmaq üçün dördbucaqlıların nəzəriyyəsi vacibdir.
Dördbucaqlıların hissələrə bölünməsi və model qurulması
Dördbucaqlını müxtəlif hissələrə bölmək və ya onun üzərində konstruksiya qurmaq olduqca maraqlı və faydalı məşğələdir. Dördbucaqlı bir və ya bir neçə üçbucağa, bərabəryanlı və qeyri-bərabər hissələrə bölünə bilər. Bu üsul həm riyaziyyatda, həm də praktiki layihələrdə sahənin bölüşdürülməsi, materialların kəsilməsi və planlaşdırmada istifadə olunur.
Məsələn, düzbucaqlı bir diaqonal üzrə iki bərabər üçbucağa, paralel iki xətt və bir kəsişən xəttlə isə müxtəlif bərabərsahəli hissələrə bölünə bilər. Model qurulmasında karton, plastmas və ya proqram təminatları ilə dördbucaqlı maketləri hazırlanır, bu da tətbiqi və yaradıcı bacarıqların formalaşmasına xidmət edir.
Dördbucaqlı ilə bağlı maraqlı faktlar və istifadə sahələri
Dördbucaqlı fiquru ilə bağlı bir sıra maraqlı faktlar var:
- Qədim riyaziyyatçılar hər dördbucaqlını iki diaqonal üzrə dörd üçbucağa bölməklə sahə hesabatı aparıblar.
- Dünyada ən qədim məlum olan torpaq bölmə planı, düzbucaqlı və kvadrat formasında hazırlanıb.
- Qrafik dizayn və vizual sənətdə ən çox istifadə olunan forma kvadrat və düzbucaqlıdır.
- Dördbucaqlıların ən mükəmməl forması kimi kvadrat həndəsədə harmoniyanın rəmzi sayılır.
Dördbucaqlıların çoxsaylı tətbiq sahələri onların gündəlik həyatda, elmdə və texnologiyada əvəzolunmazlığını sübut edir.
Dördbucaqlı həndəsənin, memarlığın, dizaynın və gündəlik həyatın ayrılmaz hissəsidir. Onun çoxşaxəli növləri, unikal xüsusiyyətləri və praktik üstünlükləri, həm riyaziyyat, həm də real tətbiq sahələrində dərin və davamlı əhəmiyyət kəsb edir. Dördbucaqlı forması həm estetik, həm funksional, həm də simvolik məna daşıyır və insan həyatının hər sahəsində öz izini qoyur.
Ən Çox Verilən Suallar
Dördbucaqlı bir düz müstəvidə yerləşən, dörd tərəfi və dörd zirvəsi olan həndəsi fiqurdur. Onun dörd daxili bucağının cəmi 360 dərəcədir, iki diagonalı, müxtəlif növ və simmetriya xüsusiyyətləri vardır.
Dördbucaqlının əsas növlərinə kvadrat, düzbucaqlı, paralelogram, romb, trapesiya və romboid daxildir. Hər növün özünəməxsus tərəf uzunluqları və bucaq xüsusiyyətləri olur.
Kvadrat və düzbucaqlı üçün sahə tərəflərin hasilinə bərabərdir. Paralelogram üçün sahə əsas tərəf ilə uyğun hündürlüyün hasilinə, trapesiya üçün isə paralel tərəflərin cəminin hündürlüyə hasilinin yarısına bərabərdir.
Dördbucaqlının perimetri bütün tərəflərinin uzunluqlarının cəminə bərabərdir. Kvadrat üçün P=4a, düzbucaqlı üçün P=2(a+b), digər növlərdə tərəflərin cəmi ilə hesablanır.
Diagonallar dördbucaqlının simmetriyasını və növünü müəyyənləşdirir. Kvadratda və düzbucaqlıda diagonallar bərabərdir, paralelogramda və rombda isə kəsişmə nöqtəsində yarıya bölünür.
Dördbucaqlı formalar memarlıqda, inşaatda, dizaynda, pəncərə və qapılarda, mebel əşyalarında, kitab və dəftər səhifələrində, ekranlarda və hətta yol nişanlarında geniş istifadə olunur.
Qədim dövrlərdən dördbucaqlı torpaq bölgüsü, bina planları və şəhərsalma üçün əsas formadır. Kvadrat sabitliyin və harmoniya, düzbucaqlı isə funksionallığın simvolu sayılır.
Dördbucaqlı bir və ya iki diaqonal üzrə üçbucaqlara, paralel və kəsişən xətlərlə bərabər sahəli hissələrə bölünə bilər. Bu, sahənin ölçülməsi və materialların bölüşdürülməsi üçün faydalıdır.
Bəzi kristal və minerallarda, bitki yarpaqlarında, heyvan bədənlərinin hissələrində, həşərat qanadlarında və təbii formalaşan strukturlarda dördbucaqlının müxtəlif növləri müşahidə olunur.
Dördbucaqlıların sahə və perimetr hesablaması torpaq ölçülərində, memarlıq və dizayn layihələrində, inşaat, riyazi modelləşdirmə və gündəlik əşya dizaynında istifadə olunur.