Qövsün dərəcə ölçüsü, tarixən Babil riyaziyyatçılarının səma müşahidələrindən bəri səmadan mexaniki qurğularadək saysız tətbiqlərə yol açan, dairəvi həndəsənin vacib elementi kimi tanınır. Tam dairənin 360 bərabər hissəyə bölünməsi bir tərəfdən astronomik dövrlərlə, digər tərəfdən 60-ın əlverişli bölən sayıyla izah olunur. Bu kəmiyyət, rəqəm və məntiqin harmoniyasını təmsil edərək məşhur sualı cavablayır: niyə bütün dairələr eyni “360” dilimə malikdir? Mövcudluğunu yalnız tarixi səbəblərə borclu olmayan dərəcə sistemi bu gün peyk naviqasiyasından yol infrastrukturuna, teleskop kalibrlərindən robotexnikaya qədər hər sahədə dəqiq bucaq ölçüsünün sinonimidir. Radian, gradian və revolyusiya kimi alternativlər mövcud olsa da, dərəcə ölçüsünün intuitiv oxunuşu ona populist üstünlük qazandırır: 90°, 120° və ya 180° üçün təsəvvür qurmaq insan beyni üçün daha təbiidir. Tənzimlənən günəş panellərindən dişli ötürücülərə, aerofotoqrafiya xəritələrindən elektron kompaslara qədər müxtəlif qurğuların etibarlı istismarı məhz dərəcə vahidinin çevikliyindən bəhrələnir. Analitik həndəsə, trigonometrik cədvəllər və diferensial tənliklər dərəcə-radian çevirmələri üzərində qurula-qurula əsrlərdir bir-birini tamamlayır. İndi həm sinif otağında, həm də yüksək dəqiqlik tələb edən laboratoriyalarda dərəcə susmaz köməkçidir: qrafik kalkulyatorlar nəticələri radianla hesablasa belə, ekranda dərəcə ilə göstərərək tələbənin təsəvvürünə baş vurur. Təlim texnologiyaları, interaktiv simulyasiya mühitləri və üçölçülü modellər dərəcə sistemini daha da əlçatan edərkən, yeni nəsil mühəndislər abstrakt formulları konkret mexanizmlərə tətbiq etməyi öyrənirlər. Beləliklə, qövsün dərəcə ölçüsü, yalnız riyazi anlayış deyil, həm də hərəkət, istiqamət və nizamın universal dilidir.
Qövs və Mərkəzi Bucaq Arasındakı Əlaqə
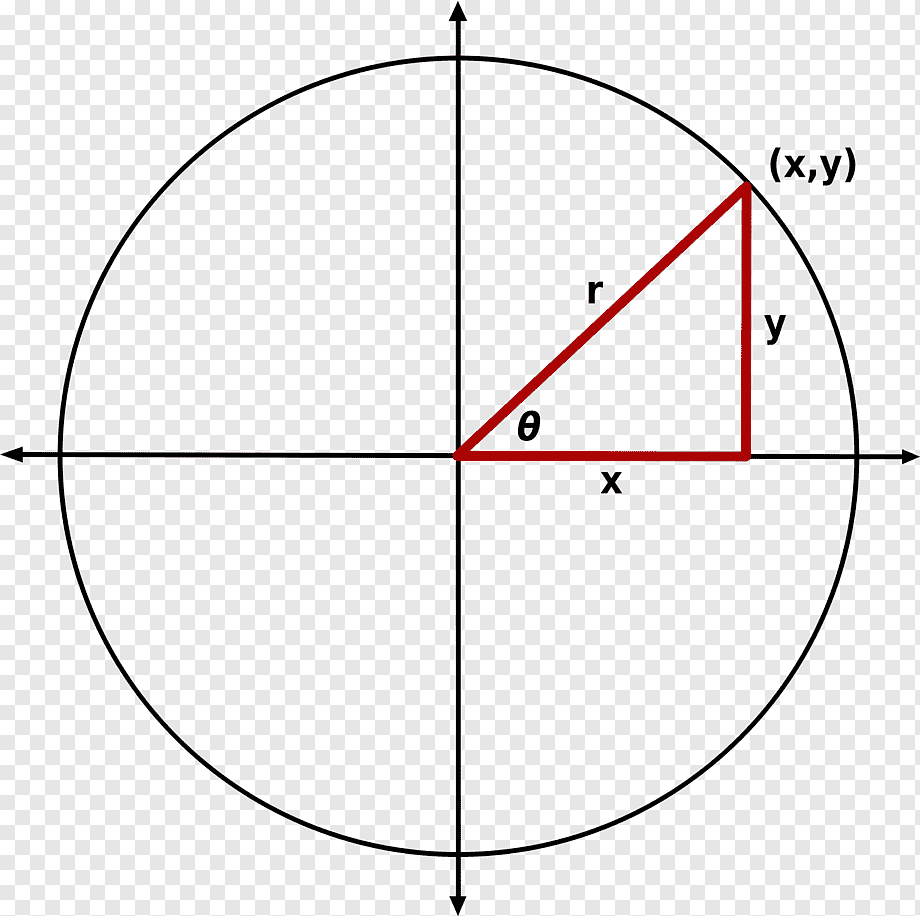
Dairənin mərkəzindən görünən hər qövs onun altında qalan mərkəzi bucaq vasitəsilə müəyyənləşdirilir və tam çevrə 360° qəbul olunduğu üçün qövsün uzunluğu bucağın dərəcə dəyərindən birbaşa asılıdır. Məsələn, çevrənin altıda bir hissəsinə bərabər qövs 60°-lik bucaq yaradır; bu sadə proporsiya məktəb riyaziyyatından kosmik mexanikayadək uzanır. Radius sabit qaldığı halda təyin olunan bucaq böyüdükcə qövs də xətti şəkildə uzanır, bu isə səthi, perimetri və hətta dairəvi sürəti hesablamaqda böyük rahatlıq verir.
Dərəcə sisteminin 360-lıq strukturunda bölənlərin çoxluğu 45°, 30°, 15° kimi praktik kəsrlərlə işləməyi asanlaşdırır və analoq cihazlarda kalibrləmə xətasını minimuma endirir. Geodeziyada koordinat şəbəkələrinin bucaq dəqiqliyi bu nisbətlərdən faydalanır; kənarlaşdırma xətası maksimum 0.1°-yə endiriləndə bir kilometr məsafədə cəmi 1.7 metr paya uyğun gəlir.
Dərəcə Ölçüsünün Tarixi İnkişafı
Qədim Babil astronomları günlərin illik dövrlərinin 360-a yaxınlığını əsas götürərək dairəni 360 hissəyə ayırdılar və bu sistem o dövrdə göy səmasının “il təqvimi” rolunu oynadı. Yunan riyaziyyatçısı Hipparx isə trigonometrik cədvəlləri tərtib edərək Babil mirasını elmi əsaslandırdı və dərəcə anlayışını rəsmi terminə çevirdi.
Orta əsr İslam alimləri, xüsusilə Əl-Biruni və Nəsirəddin Tusi, dərəcəni dəqiqə və saniyə alt bölmələrinə parçalayaraq astronomik cihazlarda tələb olunan incə düzəlişləri reallaşdırdılar. XVI əsrdə logaritm cədvəlləri çap olunduqda dərəcə bölmələri beynəlxalq elmi ünsiyyət üçün vahid üsluba çevrildi və “°” işarəsi mətbəə simvolu kimi rəsmən təsdiqləndi.
Radian Ölçüsü ilə Müqayisə
Radian radiusa dayanan təbii vahid olub, bir radianlıq bucaq radius uzunluğunda qövs yaradır; dərəcə ilə radian arasındakı əmsal π/180-dir və bu çevirmə diferensial riyaziyyatın taymlaşdırılmış funksiyalarında mühüm yer tutur. Məsələn, sin x funksiyasının törəməsi x radianla hesablanmalı olduqda, dərəcə dəyəri öncə radiana çevrilməsə, 90°-nin sinusu düzgün diferensiallşdırılmır.
Dərəcə isə gündəlik vizual təyinatlar – kompas, xəritə, ötürücü bucaqlıq – üçün daha uyğundur; bu baxımdan radianla dərəcə bir-birini tamamlayaraq həm tətbiqi, həm də nəzəri riyaziyyatda balans yaradır. Müasir kompüter qrafikası radian arqumentləri ilə işləyir, lakin istifadəçi interfeysində nəticələr dərəcə şəklində təqdim edilir ki, bu da anlaşılmanı sadələşdirir.
Qövsün Uzunluğu ilə Əlaqəli Hesablamalar
Qövs uzunluğu L = π·r·θ / 180 düsturu ilə hesablansa da, θ dərəcə ilə verilir; bu, radian istifadə etmədən gündəlik tapşırıqlar üçün rahat formuldur. Məsələn, 9 m radiuslu dairədə 120°-lik qövsün uzunluğu L = π·9·120 / 180 = 6π m olur. İnteqral hesablarda radian üstün gəlsə də, fizika və mühəndislik təcrübəsində dərəcə versiyası daha çevikdir.
Sektor sahəsi S = π·r²·θ / 360 düsturu ilə müəyyən edilir və burada θ yenə dərəcədir; bu model mexaniki mühərriklərin krank açısını təyin etməkdə, eləcə də torpaq suvarma sektorlarının dizaynında tətbiq olunur. Dərəcə dəyərinin yarıya enməsi qövs uzunluğunu və sektor sahəsini eyni nisbətdə azaldır, bu da enerjiyə qənaət hesablamalarında əhəmiyyətlidir.
| Radius (r) | Bucağın dərəcəsi (θ) | Qövs uzunluğu L = π·r·θ/180 |
|---|---|---|
| 5 m | 30° | 0.833π m |
| 5 m | 60° | 1.667π m |
| 10 m | 90° | 5π m |
| 15 m | 120° | 10π m |
Hesablama Səhvləri və Kalibrləmə
Ən geniş yayılmış xəta dərəcəni radian qəbul edərək sin, cos, tan kimi funksiyalarda bilavasitə tətbiq etməkdir; nəticədə, məsələn, sin 90 radian ≈ 0.89 hasil olur ki, bu tamamilə yanlışdır. Temperatur dəyişməsi metal komponentlərdə mikrodeformasiya yaradaraq bucağı mexaniki səviyyədə dəyişdirə bilər; sənaye sensorları bu effekti kompensasiya etmək üçün termal korreksiya cədvəllərindən istifadə edir.
Elektron kompaslarda maqnit sapmaları dərəcə göstəricisini təhrif edir və kalibrləmə prosesinə təkcə coğrafi şimal yox, həm də lokal maqnit anomaliyaları daxil edilir; bu düzəliş 0.05°-ə qədər dəqiqliklə istiqamət təyin etməyə imkan yaradır.
Tətbiq Sahələri: Astronomiya, Geodeziya, Mühəndislik
Astronomiyada Günəşin göy qübbəsində illik 360° yolu bürclərin və mövsümlərin hesablama təməlini təşkil edir; teleskopların avtomatlaşdırılmış izləmə sistemləri planetin görünən mövqelərini dərəcə azimutlarına çevirir. Geodeziyada hər 1° enlik 111 km təqribi məsafədir və bu grid ölçüsü peyk naviqasiyası üçün baza xəritə quruluşu yaradır.
Mühəndislikdə dişli ötürücülərin modul dizaynı kəsici alətlərin fırlanma bucaqlarını dərəcə vahidində tələb edir; əks halda mikrometr səviyyəsində ucluq xətaları mexanizmin titrəməsinə səbəb olur. Aviasiyada marşrut azimutları hər beş dərəcədə bir nəzərdə tutulur ki, pilot təlimat kitabçasında rəqəmlər asan oxunsun.
Riyazi Modelləşdirmə və Radian-Dərəcə Simbiozu
Numerik diferensial tənliklərin çoxu radian arqumenti tələb edir, lakin aerodinamik qanad profillərinin vizual analizi ekranda dərəcə menyuları ilə aparılır. Bu ikili sistem tələbələrin həm abstrakt, həm də praktik səviyyədə düşünmə qabiliyyətini gücləndirir.
İqlim modellərində coğrafi grid hüceyrələrinin küncləri dərəcə koordinatları ilə kodlaşdırıldıqda, meteoroloji peyk məlumatları həmin gridə yerləşdirilir və üçölçülü temperatur-sürət təhlilləri dəqiqlik qazanır. Planetar elmlərdə asteroid orbitləri həm dərəcə, həm də radian formatında bazaya yazılır ki, müxtəlif proqramlar oxu-çevirmə itkisinə yol verməsin.
Tədris Metodları və İnnovativ Platformalar
Müasir sinif otaqlarında geogebra və interaktiv lövhə proqramları şagirdlərə bucaq sürüşdürməklə qövsün real vaxtda dəyişən uzunluğunu görməyə icazə verir; bu, abstrakt həndəsəni konkret təsvirlə birləşdirir. 3D çap edilmiş mexaniki modellər tələbələrə dişli ilişmə bucağını əl ilə ölçmək şansı verir, nəticədə hesablamadakı dərəcə anlayışı fiziki təcrübə ilə möhkəmlənir.
Universitet laboratoriyalarında virtual reallıq canlandırmaları tələbələrə radial hərəkəti simulyasiya edərək radian-dərəcə çevrilməsini eyni səhnədə müşahidə etməyə imkan yaradır. Bu yanaşma həm də mühəndis dizaynı və oyun mexanikasında geniş tətbiq tapır; prototiplər daha qısa müddətdə test olunur, xəta ehtimalı azalır.
Qövsün dərəcə ölçüsü sivilizasiyanın riyazi düşüncə tərzini gündəlik həyatla birləşdirən körpü rolunu oynamaqda davam edir. Babil müşahidəçilərinin 360-lıq bölünmədən aldığı ilham bu gün peyklərin orbitini, robot qollarının fırlanmasını, həmçinin optik liflərin qırılma bucağını dəqiqliklə tənzimləyir. Bu vahid, radianla qurulan analitik modelləri sadə vizual şərhə çevirərək riyaziyyatın dilini universallaşdırır. Tarixi irs, misilsiz praktik rahatlıq və yüksək dəqiqlik tələbi sayəsində dərəcə ölçüsü bütün elmi sahələrdə öz əhəmiyyətini qoruyur. İnteraktiv öyrənmə platformaları, üçölçülü simulyasiyalar və sensor texnologiyalar dərəcə vahidini daha da əlçatan edir; yeni nəsillər sərhədsiz tətbiqlərlə hər küncdə bucağın gücünü kəşf edir. İstər avtomatlaşdırılmış günəş paneli qurğusu, istər xəritəçəkmə pilotsuz uçuş aparatı, istərsə də dalğa optikasının laboratoriyası olsun, dərəcə ölçüsü standartlaşdırılmış dil olaraq dəqiqliyi və anlaşılmanı təmin edir. Qarşıdakı dövr, pikodərəcə həssaslığına sahib sensorların və real vaxtlı VR interfeyslərin dövrü olacaq; bu isə dərəcənin həm nəzəri, həm də praktiki dəyərini yüksəldərək rəqəmsal transformasiyanın qızıl açarına çevirəcək. Tədrisdən sənayeyədək geniş spektrdə dərəcə sisteminin davamlı aktual qalması onun səmərəli, vahid və universal olduğunu sübut edir.
Ən Çox Verilən Suallar
Qövsün dərəcə ölçüsü dairənin mərkəzindən baxıldıqda qövsün altında qalan bucağın neçənci hissə olduğunu göstərir. Tam dairə 360 dərəcə kimi qəbul olunur, buna görə də 90° qövs çevrənin dörddə birini təmsil edir. Bu dəyər radiusdan asılı olmayaraq yalnız bucağın böyüklüyünü müəyyənləşdirir. Həmin dərəcə dəyəri qövs uzunluğu ilə radiusun nisbətinə görə hesablana bilər.
Dərəcəni radiana çevirmək üçün bucaq dəyərini π/180 ilə vurmaq kifayətdir. Məsələn, 60° × π/180 = π/3 radian edir. Əks çevirmə radianı 180/π əmsalına vurmaqla aparılır. Bu konversiya inteqral hesablamalarında və texniki proqramlaşdırmada vacibdir.
360 rəqəmi 1-dən 10-a qədər çoxlu bölənə sahibdir və astronomik dövrlərin 360 günə yaxın olması tarixi səbəb sayılır. Qədim Babil astronomları göyün illik hərəkətini bu sistemdə ölçərək dəqiqliyi artırmışdılar. Eyni zamanda 360°, riyazi sadəlik yaratdığı üçün sonrakı sivilizasiyalar tərəfindən də mənimsənildi. Beləliklə, həm praktik, həm də rəmzi üstünlüklər 360 sistemini sabitləşdirdi.
Bir dərəcə altmış dəqiqəyə bölünür, hər dəqiqə də altmış saniyəyə bölünür. Bu alt bölmələr qədimdən gələn altmışlıq say sistemi ilə sıx bağlıdır. Astronomiya və geodeziyada bu incə bölmələr dəqiqliyi artırır. Modern cihazlarda saniyədən daha kiçik hissələr də istifadə olunur, lakin terminologiya eyni qalır.
Qövs uzunluğu L = π·r·θ/180 düsturu ilə təyin edilir, burada r radius, θ isə dərəcə ilə verilən bucaqdır. Hesablamada θ-nın radianla verilməsi lazımdırsa, əvvəlcə dərəcəni radiana çevirmək gərəkdir. Bu düstur sektor sahəsi, dairesəl sürət və mexaniki qolların hərəkət analizində istifadə olunur. Praktik nümunələrdə radius və bucaq məlum olduqda qövs uzunluğu birbaşa tapılır.
Dərəcə vizual və praktiki sahələrdə — naviqasiya, xəritəçəkmə, mexaniki dizayn — çox rahatdır. Radian isə analitik riyaziyyatda, xüsusilə diferensial və inteqral hesablamalarda dominantdır. Kompüter qrafikasında funksiyalar radianla işləyir, amma nəticələr son istifadəçiyə dərəcə şəklində göstərilə bilər. Hər iki vahid, situasiyadan asılı olaraq, bir-birini tamamlayır.
Ən çox rast gəlinən səhv radianla işləyən trigonometriya funksiyalarında dərəcə dəyərindən istifadə etməkdir. Həmçinin bucağın istiqamətini səhv qəbul etmək azimut hesablamalarında xəta yaradır. Mexaniki hissələrdə temperatur dəyişikliyi metal uzanmasına səbəb olaraq bucaq xətası doğurur. Kalibrləmə və proqram təminatı bu xətaları minimuma endirir.
Günəş paneli sistemlərində maksimum enerji üçün ideal tilt bucağı dərəcə ilə hesablanır. Aviasiyada marşrutların azimut dərəcələri uçuş təhlükəsizliyi üçün vacibdir. Robotexnika sahəsində qolların fırlanma bucaqları dərəcə vahidində programlaşdırılır. Astronomiyada ulduzların göy sferasındakı mövqeləri də dərəcə ilə təsnif edilir.
İnteraktiv proqramlar tələbələrə bucaqları real vaxtda dəyişdirib nəticəni görməyə imkan verir. Fiziki modellər, məsələn, karton dairələr və açıqca sektorlar vizuallığı gücləndirir. Müqayisəli tapşırıqlar, yəni radianla dərəcənin eyni qövsə necə təsir etdiyini göstərmək, analitik düşüncəni inkişaf etdirir. Bu üsullar abstrakt anlayışı konkret müşahidə ilə birləşdirir.
Rəqəmsal sensor texnologiyalarının inkişafı bucaq ölçmələrində pikodərəcə dəqiqliyini real vaxtda əlçatan edəcək. Virtual reallıq sistemləri istifadəçinin baş hərəkətlərini dərəcə ilə anında ölçərək daha sərbəst interfeys yaradacaq. Autonom nəqliyyat vasitələri sensor birləşmələrində bucaq məlumatını dərəcə formatında paylaşaraq standartlaşdırılmış protokol quracaq. Bu, müxtəlif qurğular arasında universal uyğunluq təmin edəcək.