Həndəsi orta riyaziyyatda, xüsusən də həndəsə və cəbrin tətbiqi sahələrində geniş işlədilən, riyazi və praktik əhəmiyyət kəsb edən xüsusi bir anlayışdır. Bu termin müxtəlif riyazi və texniki fənlərin proqramlarında özünə möhkəm yer tutub. Həndəsi orta yalnız məktəb və universitet proqramlarında deyil, iqtisadiyyat, maliyyə, mühəndislik, texnologiya, statistik analiz və bir çox elmi tədqiqatlarda real tətbiq sahəsinə malikdir. Onun əsas fərqi, arifmetik orta ilə müqayisədə fərqli məntiqə əsaslanması, göstəricilərin hasilinin kökə çıxarılması prinsipinə söykənməsidir. Gündəlik həyatda, statistik məlumatların və müxtəlif göstəricilərin orta qiymətinin düzgün hesablanması üçün həndəsi orta əlverişli alətdir.
Riyaziyyatda orta anlayışının müxtəlif formaları var: arifmetik, həndəsi, kvadratik, harmonik və s. Lakin bəzən elə vəziyyət yaranır ki, ən doğru və obyektiv qiymətləndirmə yalnız həndəsi orta vasitəsilə mümkündür. Həndəsi orta çox vaxt göstəricilərin multiplikativ əlaqədə olduğu, fərqli faizlər və artım-templərlə işlənilən məsələlərdə tətbiq edilir. Bəs həndəsi orta nəyə əsaslanır, necə hesablanır, hansı xüsusiyyətləri və tətbiq sahələri var?
Həndəsi orta anlayışının mahiyyəti
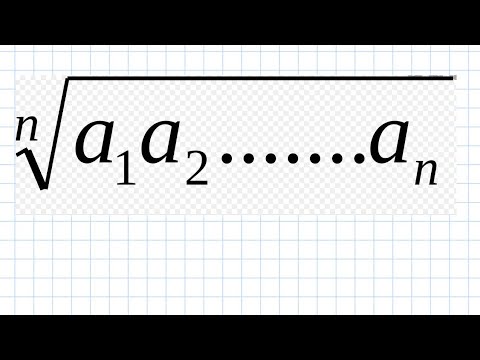
Həndəsi orta (geometrik orta) bir neçə müsbət ədəddən ibarət dəstin “ümumi artım əmsalı” kimi çıxış edən, bütün ədədlərin hasilinin kökünə bərabər olan bir ədəddir. Riyazi dildə desək, n sayda müsbət a₁, a₂, …, aₙ ədədləri üçün həndəsi orta aşağıdakı düsturla hesablanır:
G=a1⋅a2⋯annG=na1⋅a2⋯an
Bu formulda G – həndəsi ortadır, n – ədədlərin sayıdır, a₁, a₂, …, aₙ – uyğun ədədlərdir.
Məsələn, 2, 8, 18 ədədlərinin həndəsi ortasını hesablamaq üçün:
G=2⋅8⋅183=2883≈6.6G=32⋅8⋅18=3288≈6.6
Bu misal göstərir ki, həndəsi orta hər üç ədədin artım nisbətini bərabərləşdirən universal qiymət təklif edir.
Həndəsi orta və arifmetik orta
Çoxları üçün “orta” dedikdə ən əvvəl arifmetik orta ağla gəlir. Halbuki, həndəsi orta fərqli prinsipə əsaslanır və müəyyən hallarda arifmetik ortadan tamamilə fərqli nəticələr verə bilər. Əsas fərqlər belədir:
| Xüsusiyyət | Arifmetik Orta | Həndəsi Orta |
|---|---|---|
| Hesablama qaydası | Cəmin ədədlərin sayına bölünməsi | Hasilin kökə çıxarılması |
| Müsbət ədədlər | İstənilən ədədlərdə | Yalnız müsbət ədədlərdə tətbiq oluna bilər |
| İstifadə sahəsi | Sabit artım/azalma olmayan hallarda | Multiplikativ, faizli, artımlı hallar |
| İzahlı nümunə | (a₁+a₂+…+aₙ)/n | a1⋅a2⋯annna1⋅a2⋯an |
Bu cədvəl həndəsi orta və arifmetik ortanın əsas fərqini və onların tətbiq sahələrini aydın göstərir.
Həndəsi ortanın riyazi və məntiqi əsaslandırılması
Həndəsi ortanın əsaslandığı məntiq ondan ibarətdir ki, bir neçə göstəricinin bərabər artım və ya azalma nisbətini tapmaq lazımdırsa, yalnız bu üsul real “bərabərləşdirici” qiymət verir. Xüsusən də, faiz artımı və ya multiplikativ effektin toplandığı hallarda bu, ən dəqiq nəticədir.
Məsələn, ardıcıl illərdə bir investisiyanın gəliri 10%, 20%, 30% olursa, orta illik gəlirlilik arifmetik yox, həndəsi orta ilə tapılır:G=1.1⋅1.2⋅1.33≈1.195G=31.1⋅1.2⋅1.3≈1.195
Burada nəticə “ortalama illik artım əmsalı”nı göstərir.
Həndəsi ortanın tətbiq sahələri
Həndəsi orta bir çox riyazi, texniki, iqtisadi və statistik məsələlərdə tətbiq edilir:
- İqtisadiyyat və maliyyə: Orta illik artım və gəlirlik dərəcələrinin, portfel üzrə orta faizlərin hesablanması.
- Statistika və analiz: Multiplikativ indekslərin, ölçü vahidlərinin orta qiymətlərinin tapılması.
- Həndəsə və riyaziyyat: Müxtəlif fiqurlarda, məsələn, düzbucaqlı üçbucağın daxili dairəsinin radiusunu hesablamaq üçün.
- Fizika və kimya: Miqdarı sürətlə dəyişən və ya artan/azalan göstəricilərin analizində.
- Əhalinin artımı: Fərqli dövrlərdə fərqli artım sürətlərinin orta illik göstəricisinin tapılması.
Həndəsi ortanın əsas xüsusiyyətləri
Həndəsi orta yalnız müsbət ədədlər üçün məna kəsb edir. Sıfır və ya mənfi ədəd daxil edildikdə nəticə ya sıfır olur, ya da real ədədlər toplusunda mümkün olmur. Həndəsi orta həmişə arifmetik ortadan kiçik və ya ona bərabər olur. Bərabərlik yalnız bütün ədədlər bərabər olduqda mümkündür.
Bundan başqa, həndəsi orta ədədlərin böyük-dən kiçiyə və ya kiçik-dən böyüyə düzülməsindən asılı olmur, nəticə eyni qalır. Həndəsi ortanın başqa bir önəmli xüsusiyyəti: multiplikativ xarakterli seriyalarda, dəyişmə diapazonu geniş olan göstəricilərdə daha obyektiv və həssas nəticə verməsidir.
Həndəsi ortanın nümunə ilə izahı
Təsəvvür edin, bir məhsulun qiyməti 3 il ardıcıl olaraq belə dəyişib: əvvəl 100 manat, sonra 120 manat, daha sonra isə 150 manat. Orta artımı hesablamaq üçün həndəsi orta belə tapılır:G=100⋅120⋅1503≈1,800,0003≈122.5G=3100⋅120⋅150≈31,800,000≈122.5
Deməli, hər il məhsulun qiymətinin təxminən 22.5% artımı müşahidə olunub.
Fərqli vəziyyətlərdə həndəsi ortanın tətbiqi
Bəzən faizlə ifadə olunan illik artım və azalma dərəcələri həndəsi ortanın vacibliyini daha aydın göstərir. Əgər bir investisiya bir il 20%, növbəti il 40% qazanc gətirirsə, orta gəlir sadə ortadan fərqli alınır:
- Arifmetik orta: (20%+40%)/2 = 30%
- Həndəsi orta: 1.2⋅1.4−1=1.68−1≈0.296=29.61.2⋅1.4−1=1.68−1≈0.296=29.6
Bu misal multiplikativ artımda həndəsi ortanın üstünlüyünü göstərir.
Həndəsi ortanın hesablama üsulları və mərhələləri
Həndəsi orta aşağıdakı addımlarla tapılır:
- Bütün ədədlər hasil şəklində birləşdirilir.
- Əldə olunan hasil n-ci dərəcədən kökə çıxarılır (n – ədədlərin sayıdır).
- Nəticə müvafiq kontekstdə şərh edilir.
Cədvəldə müxtəlif hallar üçün formul və nümunə göstərilib:
| Hal | Düstur | Nümunə | Nəticə |
|---|---|---|---|
| 2 ədəd üçün | G=a1⋅a2G=a1⋅a2 | G=4⋅9G=4⋅9 | G=6G=6 |
| 3 ədəd üçün | G=a1⋅a2⋅a33G=3a1⋅a2⋅a3 | G=2⋅8⋅183G=32⋅8⋅18 | G≈6.6G≈6.6 |
| n ədəd üçün | G=a1⋅…⋅annG=na1⋅…⋅an | G=2⋅4⋅8⋅324G=42⋅4⋅8⋅32 | G=8G=8 |
Həndəsi ortanın statistik və iqtisadi təhlildə rolu
Həndəsi orta statistik göstəricilərin bərabər “çoxalması” və ya “azalması” hallarının obyektiv dəyərləndirilməsi üçün istifadə olunur. Məsələn, inflyasiya göstəriciləri, indekslər, gəlirlilik və məhsuldarlıq, əhali artımı kimi sahələrdə ən doğru təhlil həndəsi ortadan keçir.
Bundan əlavə, maliyyə portfeli üzrə müxtəlif aktivlərin orta illik gəlirliliyi, faiz və indeks dinamikası da həndəsi ortadan istifadə ilə daha obyektiv ölçülür.
Həndəsi ortanın digər orta növləri ilə müqayisəsi
Fərqli hallar üçün orta seçimi böyük əhəmiyyət kəsb edir. Aşağıdakı cədvəldə orta növlərinin əsas fərqləri göstərilib:
| Orta növü | Düstur | İstifadə sahəsi |
|---|---|---|
| Arifmetik orta | (a1+…+an)/n(a1+…+an)/n | Sabit artım, sadə hallar |
| Həndəsi orta | a1…annna1…an | Artım, faiz, indekslər |
| Kvadratik orta | (a12+…+an2)/n(a12+…+an2)/n | Sürət, enerji, fizika |
| Harmonik orta | n/(1/a1+…+1/an)n/(1/a1+…+1/an) | Sürət, orta məsafə, yol |
Riyaziyyatda və həyatda həndəsi ortanın tətbiqi
- Əhalinin illik artımı: Bütün illik artım əmsallarının həndəsi ortası uzunmüddətli artım tempini göstərir.
- İnvestisiya gəlirliliyi: Fərqli illərdə müxtəlif gəlir dərəcəsi olan investisiyalarda uzunmüddətli orta gəliri hesablamaq üçün.
- Elm və texnologiya: Multiplikativ dəyişənlərlə bağlı məsələlərdə.
- Fizika və kimya: Maddə miqdarlarının artım və azalması proseslərində.
Həndəsi orta riyaziyyatın, statistikanın və iqtisadiyyatın ən önəmli anlayışlarından biridir. Onun köməyi ilə artım və azalma dinamikası obyektiv şəkildə ölçülür, real və tətbiqi nəticələr əldə edilir. Həndəsi ortanın düzgün seçilməsi və tətbiqi analitik düşüncə, elmi dəqiqlik və obyektiv yanaşma üçün əsas şərtdir. Hər bir tələbə, iqtisadçı, mühəndis və menecer üçün bu anlayışı dərindən mənimsəmək və tətbiq bacarığını inkişaf etdirmək müasir dövrdə zərurətə çevrilib.
Ən Çox Verilən Suallar
Həndəsi orta bir neçə müsbət ədədin hasilinin həmin ədədlərin sayında kökünə bərabər olan riyazi göstəricidir; multiplikativ artım və faizli dəyişmələr üçün istifadə edilir.
n ədəd üçün həndəsi orta: G = (a₁ × a₂ × … × aₙ)^(1/n) formasında hesablanır.
Ən çox multiplikativ artım, faiz dəyişiklikləri, indeks və illik gəlirlilik kimi sahələrdə tətbiq edilir.
Arifmetik orta ədədlərin cəminin sayına bölünməsidir, həndəsi orta isə hasilin kökünə çıxarılması ilə tapılır; multiplikativ artımda həndəsi orta daha düzgün nəticə verir.
Yalnız müsbət ədədlər üçün məna kəsb edir, mənfi və sıfır ədədlərdə riyazi olaraq nəticə yoxdur və ya real deyil.
Əhali artımı, inflyasiya, investisiya gəlirliliyi, məhsul qiymətlərinin orta artım templəri və digər sahələrdə geniş tətbiq edilir.
Həndəsi orta həmişə arifmetik ortadan kiçik və ya ona bərabər olur; yalnız bütün ədədlər bərabər olduqda bərabərlik mümkündür.
Çünki artım və dəyişmə sürətinin obyektiv təhlili, xüsusən multiplikativ dəyişənlərdə, yalnız həndəsi ortadan istifadə ilə düzgün qiymətləndirilir.
Maliyyə, iqtisadiyyat, demoqrafiya, texnologiya, riyaziyyat, fizika və kimyada geniş tətbiq sahəsi var.
Bütün müsbət ədədlər hasilə vurulur, sonra n-ci dərəcədən kökə çıxarılır; praktikada kalkulyator və ya proqram vasitəsilə rahat hesablanır.