İrrasional Ədədlər: Yaranması, Əsas Xüsusiyyətləri

Riyaziyyat elmi insan həyatının müxtəlif sahələrində əsaslı rol oynayan və zaman-zaman inkişaf edən çoxşaxəli bir sahədir. Bu sahənin ən fundamental anlayışlarından biri də ədədlər sistemidir. Ədədlər insanın saymaq, ölçmək, hesablamaq və dünyanı təsvir etmək kimi gündəlik fəaliyyətlərinin təməlini təşkil edir. Lakin ədədlər yalnız sadə saymaq vasitəsi olmaqla kifayətlənmir; onlar riyaziyyatın dərinliyinə doğru uzanan müxtəlif kateqoriyalar və alt-sistemlər yaradır. Bunlardan biri də irrasional ədədlərdir ki, onlar ədədlərin kompleks və zəngin quruluşunu göstərməkdə xüsusi əhəmiyyət daşıyır.

İrrasional ədədlər, riyaziyyatın ən qədim və ən maraqlı kəşflərindən sayılır. Onların mövcudluğu və təbiəti insan düşüncəsində ədədlərin təbiətinə dair ənənəvi və uzun müddət qəbul edilmiş fikirləri kökündən dəyişib. İnsanlar əsrlər boyu ədədləri tam ədədlər və onların sadə fraksiyaları kimi qavrayırdılar və hesab edirdilər ki, hər hansı ədəd rasionallıqla ifadə edilə bilər. Lakin təbiətdə və riyazi modellərdə ortaya çıxan bəzi ölçülərin, məsafələrin və həndəsi əmsalların belə ifadə edilə bilməməsi riyaziyyatın fundamental prinsiplərinə yenidən baxmağa səbəb oldu.

İrrasional ədədlər — onluq kəsr şəklində ifadə olunduqda sonsuz və təkrarlanmayan, həmçinin sadə fraksiya kimi təmsil olunmayan ədədlərdir. Bu ədədlərin ən məşhurları arasında π\piπ (dairənin çevrəsinin diametrinə nisbəti), eee (təbii logaritmin əsası), və kökdə 2 ​ kimi kvadrat köklər yer alır. Bu ədədlər elmdə, texnologiyada, mühəndislikdə və gündəlik həyatda çox geniş istifadə olunur və riyazi analiz, həndəsə və digər sahələrdə vacib rol oynayır.

İrrasional ədəd nədir?

İrrasional ədəd — ədədlər sistemində rasionallığa aid olmayan, yəni iki tam ədədin nisbəti kimi yazıla bilməyən real ədədlərdir. Başqa sözlə, əgər x ədədi aşağıdakı kimi ifadə edilə bilmirsə:

x = p / q

burada p və q tam ədədlərdir və q sıfır deyil, deməli x irrasional ədəddir. İrrasional ədədlərin onluq təsviri sonsuzdur və heç bir təkrarlanan dövrə malik deyil.

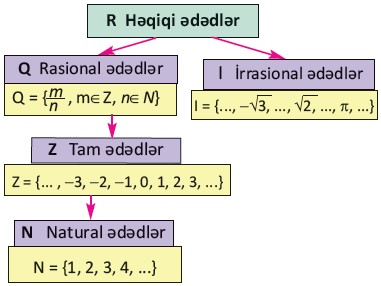
İrrasional ədədlərin yaranması və tarixi

İrrasional ədədlərin kəşfi qədim yunan riyaziyyatçılarına, xüsusilə Pifaqor məktəbinə aid edilir. Pifaqorlar üçün bütün ədədlər rasional idi və onlar hesab edirdilər ki, hər uzunluq iki tam ədədin nisbəti kimi ifadə edilə bilər. Lakin hipotenusun uzunluğunun bir kənarın uzunluğuna nisbəti kimi çıxan √2-nin rasionallıqla ifadə olunmadığı sübut olunanda, bu fikirlər dəyişdi. Bu hadisə irrasional ədədlərin riyaziyyatda mövcudluğunun ilk təsdiqi kimi qəbul edilir.

Sonrakı dövrlərdə daha mürəkkəb irrasional ədədlər, məsələn π və e, tədricən elmi ictimaiyyət tərəfindən qəbul edildi. İrrasional ədədlərin elmi tədqiqi riyaziyyatın inkişafında böyük rol oynayıb.

İrrasional ədədlərin əsas xüsusiyyətləri

• Fraksiya şəklində ifadə edilə bilməzlər.
• Sonsuz onluq ifadəyə malikdirlər.
• Sonsuz saydadırlar.
• Cəbrik və transsendent növləri vardır.
• Riyazi analizdə mühüm rol oynayırlar.

İrrasional ədədlərin növləri

1. Cəbrik irrasional ədədlər: müəyyən cəbrik tənliyin kökü olan, amma rasional olmayan ədədlər (məsələn √2, √3).
2. Transsendent irrasional ədədlər: heç bir cəbrik tənliyin kökü olmayan ədədlər (məsələn π, e).

İrrasional ədədlərin məşhur nümunələri

• Kvadrat köklər: √2, √3, √5
• Pisay sayı: π
• Neyperin ədədi: e
• Qızılı kəsr: φ = (1 + √5)/2 ≈ 1.61803

İrrasional ədədlərin təqribi dəyərləri və hesablanması

• π ≈ 3.1415926535…
• e ≈ 2.7182818284…
• √2 ≈ 1.4142135623…

İrrasional ədədlərin riyaziyyatdakı rolu

• Analizdə (limitlər, sonsuz cəmlər)
• Həndəsədə (dairəvi ölçülər)
• Cəbrdə (polinom tənliklər)
• Riyazi fizika və digər sahələrdə

İrrasional ədədlər və təhsil

Məktəblərdə və universitetlərdə irrasional ədədlərin anlayışı əsas mövzudur. Onların tərifi, misalları, xüsusiyyətləri və tətbiqləri tədris edilir.

İrrasional ədədlərin tətbiq sahələri

• Mühəndislik
• Fizika
• İqtisadiyyat
• Kompüter elmləri
• Memarlıq və incəsənət

İrrasional ədədlər riyaziyyatın ən dərin və maraqlı anlayışlarından biridir və bu anlayışın inkişafı insanlıq tarixində riyaziyyat elminin əhəmiyyətli mərhələlərindən sayılır. Bu ədədlər bizə real dünyada qarşılaşdığımız mürəkkəb riyazi və fiziki anlayışları daha düzgün və dəqiq təsvir etməyə imkan verir. İrrasional ədədlər, öz sonsuz və təkrarsız onluq təsvirləri ilə riyazi analiz və cəbrin əsasını təşkil edir, funksiyaların limitləri, diferensial tənliklərin həlləri, həndəsənin əsas parametrləri kimi sahələrdə geniş tətbiq olunur.

Ədədi sistemin zənginliyi və kompleksliyi irrasional ədədlər olmadan təsəvvür edilə bilməz. Onların olması sayəsində, riyaziyyat yalnız sadə rasionallıqdan ibarət olmur, daha mürəkkəb və təbiətdə real müşahidə edilən hallara uyğun modelləşdirilə bilir. Məsələn, dairənin çevrəsi ilə diametri arasındakı əlaqəni göstərən π\piπ, təbii artım proseslərinin əsasını təşkil edən eee və çoxsaylı kvadrat köklər həyatımızın hər sahəsində qarşımıza çıxır.

Bundan əlavə, irrasional ədədlərin təbiətdə və incəsənətdə özünü göstərməsi onların universal və fundamental mahiyyətinə işarə edir. Qızılı kəsrin (φ) müxtəlif təbiət formalarında və insan estetik duyğusunda rolu buna bariz nümunədir.

Müasir riyaziyyatda irrasional ədədlər həm elmi tədqiqatların, həm də praktiki tətbiqlərin vacib komponentidir. Kompüter elmləri, mühəndislik, fizika, iqtisadiyyat və digər sahələrdə bu ədədlər olmadan dəqiq hesablamalar və modelləşdirmələr aparmaq mümkün deyil. İrrasional ədədlərin sonsuzluğu və təkrarsızlığı riyazi fikrin sərhədlərini genişləndirir və yeni nəzəriyyələrin yaranmasına şərait yaradır.

Təhsil sistemində irrasional ədədlərin mövqeyi isə xüsusilə əhəmiyyətlidir. Onların anlayışı riyazi düşüncənin inkişafına və kritik analiz qabiliyyətinin formalaşmasına töhfə verir. Şagird və tələbələrə bu anlayışların dərin izahı gələcəkdə elmi və texnoloji kəşflərin əsasını təşkil edir.

Ümumilikdə, irrasional ədədlər insan ağlının riyazi təfəkkürünün inkişafında çox vacib mərhələ olub, həm nəzəri, həm də praktik səviyyədə həyatımıza dəyər qatır. Onların öyrənilməsi və istifadəsi gələcəkdə də riyaziyyat və digər elmlərin inkişafında əsas katalizator olacaq.

Ən Çox Verilən Suallar