İti Bucaq: Riyaziyyatda, Həndəsədə Tətbiqi

Riyaziyyatda bucaqlar əsas həndəsi anlayışlardan biridir və müxtəlif növ bucaqlar arasında iti bucaq xüsusi yer tutur. İti bucaq, ölçüsü 0 dərəcədən böyük, 90 dərəcədən kiçik olan bucaq kimi təyin olunur. Başqa sözlə, iki şüa arasında yaranan və 90 dərəcədən az olan bucağa iti bucaq deyilir. Riyaziyyat dərslərində ilk dəfə bu anlayışla qarşılaşanda, çox vaxt uşaqlar bucaq ölçüləri arasında fərqləri anlamaqda çətinlik çəkirlər. Lakin, düzgün izah və praktiki nümunələr bu məsələni daha anlaşıqlı edir. İti bucaq həyatımızda və ətraf aləmdə saysız-hesabsız nümunələrlə rast gəlinir: bıçağın ucu, qələmin iti ucu, bəzi tikililərin dekorasiyasında, təbiətdə yarpaqların və daşların uclarında və s.

İti bucaqlar yalnız elementar həndəsə üçün deyil, həmçinin trigonometriya, cəbr və fizika kimi digər riyazi və elmi sahələr üçün də əsas rol oynayır. Hər bir üçbucağın ən azı iki bucağı itidir və məhz bu xassə üçbucaqların təsnifatında, düzbucaqlı və kəskinbucaqlı üçbucaqların öyrənilməsində baza rolunu oynayır. Riyaziyyatda doğru, geniş, tam və iti bucaqlar müxtəlif sahələrdə obyektlərin və fiqurların xassələrinin öyrənilməsinə imkan yaradır. İti bucaq anlayışının mənimsənilməsi, sonrakı riyazi mövzuların, xüsusilə də trigonometriyanın, sinus, kosinus, tangens və kotangens kimi funksiyaların əsasını təşkil edir.

İti Bucağın Riyaziyyatda və Həndəsədə Tətbiqi

İti bucaqların riyaziyyatda ən çox rast gəlinən tətbiq sahələrindən biri üçbucaqların növlərinin təsnifatıdır. Əgər bir üçbucağın bütün bucaqları 90 dərəcədən kiçikdirsə, bu üçbucaq “kəskinbucaqlı üçbucaq” adlanır. Yəni, belə üçbucaqlarda hər üç bucaq itidir. Əgər üçbucaqlardan biri düzdürsə (90°), onda həmin üçbucaq “düzbucaqlı üçbucaq” adlanır, digər iki bucaq isə mütləq itidir. Bundan əlavə, həndəsi fiqurların xassələri, konstruksiyaların dayanıqlığı, tikinti və memarlıq layihələrində də iti bucaqlardan geniş istifadə olunur.

Trigonometriyada isə bu bucaqlar əsas anlayışların formalaşmasında mühüm rol oynayır. Trigonometriya funksiyaları (sinus, kosinus, tangens, kotangens) ən çox məhz iti bucaqlar üçün hesablanır və tətbiq olunur. Məsələn, düzbucaqlı üçbucaqlarda bucaqların qarşısındakı katetin və hipotenuzun nisbətləri yalnız iti bucaqlarla bağlı olur. Riyaziyyatda bu kimi funksiyaların tətbiqi, həndəsi problemlərin həlli, məsafə və hündürlüyün ölçülməsi, optikada işığın qırılması, fizikanın mexanika bölməsində qüvvələrin parçalanması, mühəndislikdə müxtəlif ölçü və hesablamalar da məhz bu anlayışa əsaslanır.

İti Bucağın Həyatımızdakı Praktik Nümunələri və Əhəmiyyəti

İti bucaqlar gündəlik həyatda ən çox rast gəlinən həndəsi elementlərdəndir. Ətrafımıza diqqətlə baxsaq, bucaqları 90 dərəcədən kiçik olan çoxlu fiqur və obyektlər görmək mümkündür. Məsələn, kəskin bıçaq və qayçı ucları, küncdə qoyulmuş riyazi cizgilər, bəzi pəncərə və qapı dizaynları, təbiətdəki yarpaq və dağ yamaclarının kəskin ucluğu, uşaq oyuncaq qurğularının bəzi detalları və s. İti bucaqlar bəzən təhlükəli, bəzən isə funksional və gözoxşayan dizayn elementləri kimi çıxış edir.

Müasir dizaynda, memarlıqda və sənayedə də iti bucaqlardan istifadə xüsusi estetik və texniki üstünlüklər verir. Məsələn, aviasiya və avtomobil sənayesində aerodinamik fiqurlar, yol nişanları, bəzi texnoloji qurğular, hətta mobil telefon və kompüter korpuslarının dizaynı iti bucaqların düzgün seçimi ilə müəyyən edilir. İti bucaqlar işıq və səs dalğalarının qırılması, bəzən də enerjinin bir nöqtəyə toplanması kimi effektlər üçün də istifadə olunur. İnsanların gündəlik həyatında isə iti bucaqların düzgün və təhlükəsiz istifadəsi üçün maarifləndirmə tədbirləri aparılır, çünki bəzən bu bucaqlar uşaqlar və həssas qruplar üçün risk yarada bilər.

Riyaziyyat və Elmdə İti Bucaqların Xüsusi Xassələri

İti bucaqların riyaziyyat və elmdə araşdırılması zamanla daha dəqiq və funksional yanaşmaların formalaşmasına səbəb olub. İti bucaqların əsas xüsusiyyəti – ölçüsünün 0 dərəcədən böyük, 90 dərəcədən kiçik olmasıdır. İti bucağın sinusu və kosinusu həmişə müsbət qiymət alır, tangens və kotangens funksiyaları isə məhdud aralıqda dəyişir. Bütün bucaqlar arasında ən iti (ən kiçik) bucaq “minumum bucaq” kimi müəyyən edilir. Məsələn, mühəndislikdə, optikada, mexanikada və müxtəlif cihazlarda bu xüsusiyyətlərdən istifadə edilir.

Həmçinin, “bucaqların cəmi” anlayışı üçbucaq və çoxbucaqlılarla bağlı məsələlərdə fundamental rol oynayır. Üçbucağın daxilindəki hər bir bucağın cəmi 180 dərəcə olur və bu üç bucağın ən azı ikisi mütləq itidir. Riyaziyyatda, bəzən ən qısa yol və minimal məsafə tapmaq üçün iti bucaqlardan istifadə olunur. İti bucaq həmçinin, çoxbucaqlı fiqurların daxili bucaqlarının hesablanmasında da əsas rol oynayır.

İti Bucağın Riyaziyyatda Əhəmiyyəti və Üçbucaqlardakı Rolu

Riyaziyyatda bucaqların əsas təsnifatında iti bucaqlar xüsusi əhəmiyyət kəsb edir. İti bucaq, 0 dərəcədən böyük, 90 dərəcədən kiçik olan bucaqdır. Bu intervalda yerləşən bütün bucaqlara iti bucaq deyilir və bu anlayış həndəsənin, xüsusilə də üçbucaqların əsas strukturlarından birini təşkil edir. Üçbucağın hər hansı bir bucağı 90 dərəcədən az olduqda, həmin bucaq itidir və üçbucağın növünə təsir edir. Əgər üçbucağın hər üç bucağı iti olarsa, bu “kəskinbucaqlı üçbucaq” adlanır. Əgər bir bucaq düz (90°), digər ikisi isə itidirsə, bu tip “düzbucaqlı üçbucaq” adlanır. Ümumilikdə, hər üçbucağın ən azı iki bucağı itidir və bu, bu fiqurun həndəsi sabitliyini təmin edən mühüm xüsusiyyətdir.

İti bucaqlar riyazi düşüncənin formalaşmasında və elmi yanaşmaların inkişafında da baza rolunu oynayır. Onların öyrənilməsi sadəcə həndəsə ilə məhdudlaşmır, həm də trigonometriya, cəbr, fizika və texnologiya fənlərində tətbiq tapır. Trigonometriyada sinus, kosinus, tangens və kotangens kimi funksiyalar məhz iti bucaqlar üçün ən praktik şəkildə izah olunur. Düzbucaqlı üçbucaqlarda hipotenusun, katetin və bucağın qarşı və bitişik tərəfinin nisbətləri, sinus-kosinusa əsaslanan hesablamalar və cəbrə keçidlər üçün iti bucağın rolu əvəzolunmazdır. Bütün bunlar göstərir ki, iti bucağın riyaziyyatdakı yeri həm nəzəri, həm də praktiki baxımdan vacib və əsaslıdır.

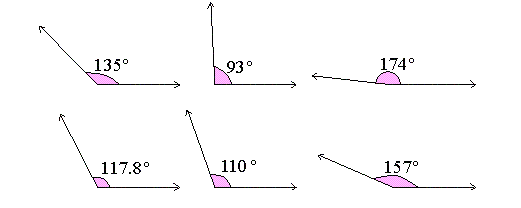
İti Bucaqların Gündəlik Həyatda və Texnologiyada Praktik Əhəmiyyəti

İti bucaqlar təkcə riyazi abstraksiya deyil, həm də gündəlik həyatımızda və texnoloji inkişafda aktiv rol oynayan həndəsi elementlərdir. Ətrafımıza diqqət etsək, iti bucaqları müxtəlif sahələrdə görmək mümkündür. Məsələn, bıçaq və qayçıların iti ucu, bəzi mebel və interyer dizaynları, pəncərə çərçivələri, dekorativ elementlər, hətta bəzi maşın və texniki qurğuların kəskin bucaq altında dizayn edilmiş detallarında bu formaya rast gəlirik. Bu cür dizaynlar bəzən funksionallığı, bəzən isə estetik gözəlliyi artırır. Aerodinamika və avtomobil dizaynında isə iti bucaqlar hava müqavimətini azaltmaq, sürəti və yanacaq səmərəliliyini artırmaq üçün vacibdir. Eyni zamanda, mobil telefon, kompüter və digər elektron cihazların korpusunda iti bucaqlar həm müasir görünüş, həm də rahat tutuş üçün xüsusi olaraq seçilir.

İti Bucaqların Ölçülməsi və Praktik Yoxlanılması

Bucaqların ölçülməsi üçün ən çox istifadə olunan alət qonur və ya “transportir” adlanır. Müasir texnologiya və elmi tədqiqatlarda bucaqlar xüsusi elektron cihazlar, bucaqölçən proqramlar və hətta lazer ölçü sistemləri ilə də ölçülür. Riyaziyyat dərslərində isə şagirdlər sadə alətlərlə – kağız, xətkeş və transportir vasitəsilə iti bucaqları ölçməyi öyrənirlər. İti bucağın ölçülməsi üçün onun başlanğıc nöqtəsi və iki şüası arasında olan açı dərəcə ilə müəyyən edilir. Əgər bucağın ölçüsü 0-90° arasındadırsa, deməli bu, iti bucaqdır.

Bəzən iti bucaqların ölçülməsində yanlışlıqlar ola bilər, çünki gözdən kiçik görünən hər bucaq mütləq iti olmur. Ona görə də, bucağın dəqiq ölçülməsi üçün xüsusi yanaşma və texniki vasitələr lazımdır. Praktikada iti bucaqları yoxlamaq üçün bəzən “düzbucaqlı üçbucaq” istifadə edilir: üçbucağın bir bucağı düz (90°), digər iki bucağı isə mütləq itidir. Bu yanaşma, həm riyaziyyat tədrisində, həm də texniki layihələrdə dəqiqliyi təmin edir.

Riyaziyyatda İti Bucaqlar və Trigonometrik Funksiyalar

Trigonometrik funksiyalar (sinus, kosinus, tangens, kotangens) əsasən iti bucaqlarla əlaqədardır. Xüsusilə, düzbucaqlı üçbucaqlarda iti bucaqlar üçün bu funksiyaların qiymətləri hesablanır. Sinus funksiyası iti bucağın qarşısında yerləşən katetin hipotenuza nisbətidir, kosinus isə bitişik katetin hipotenuza nisbəti kimi müəyyən edilir. Tangens və kotangens isə qarşı və bitişik katetlərin nisbətləri əsasında hesablanır. Riyaziyyat dərslərində bu funksiyalar şagirdlərə iti bucaqlar üzərində əyani və praktiki nümunələrlə izah olunur.

Trigonometrik funksiyaların əsas xassəsi ondan ibarətdir ki, iti bucağın dəyəri artdıqca sinusun qiyməti artır, kosinusun isə əksinə azalır. Tangens və kotangens funksiyaları isə 0°-90° aralığında müxtəlif sürətlə dəyişir və riyazi hesablamalarda geniş tətbiq olunur. Trigonometriya yalnız həndəsi məsələlər üçün deyil, həm də fizika, astronomiya, geodeziya, memarlıq və mühəndislik kimi elmi və texniki sahələr üçün də əsas vasitədir.

İti Bucaqların Müasir Elm və Texnologiyada Rolu

Bugünkü müasir elm və texnologiyada iti bucaqların tətbiqi çox genişdir. Kompüter qrafikası, 3D modelləşdirmə, optik cihazların dizaynı, lazer texnologiyaları, mobil cihazların sensor sistemləri və robot texnologiyalarında bu bucaqlardan istifadə olunur. İnşaat və memarlıqda konstruksiyaların dayanıqlığının hesablanmasında, körpülərin və yüksək binaların layihələndirilməsində iti bucaqlar xüsusi yer tutur. İti bucaqlar enerjinin yayılması, səs və işıq dalğalarının qırılması, optik prizmalarda işığın sındırılması, tibbi cihazlarda və hətta kosmik tədqiqatlarda geniş tətbiq tapır.

Bu bucaqların hesablanması və tətbiqi texniki təhlükəsizlik, enerji səmərəliliyi və yüksək dəqiqlik tələb edən layihələrdə əsas şərtlərdəndir. Müasir kompüter proqramları, CAD (Computer Aided Design) proqramları vasitəsilə çox mürəkkəb konstruksiyalarda belə iti bucaqlar asanlıqla müəyyən və təhlil edilir. Bütün bu nümunələr göstərir ki, iti bucaqlar yalnız riyazi anlayış deyil, həm də texnoloji və sənaye inqilabının vacib elementlərindən biridir.

İti bucaqlar riyaziyyat, elm, texnologiya və gündəlik həyatın ayrılmaz hissəsidir. Bu anlayışın düzgün mənimsənilməsi, şagird və tələbələr üçün gələcək elmi və texniki biliklərin təməlini qoyur. Müasir dövrün tələbləri və texnologiyanın inkişafı iti bucaqların daha da geniş istifadəsini şərtləndirir. Memarlıqdan tutmuş, sənayeyə, gündəlik məişət əşyalarından tutmuş, optik cihazlara qədər hər yerdə iti bucaqların təsiri və əhəmiyyəti müşahidə olunur. Bu mövzunun düzgün və praktiki öyrədilməsi həm məktəbdə, həm də peşəkar həyatda uğurlu nəticələr verir. İti bucağın sadə, lakin funksional mahiyyəti insanlara riyazi dünyanı və təbiəti daha yaxşı başa düşmək imkanı yaradır.

Ən Çox Verilən Suallar