Riyaziyyatın ən qədim anlayışlarından biri olan qövsün dərəcə ölçüsü gündəlik həyatın çoxsaylı sahələrində görünmədən iştirak edir. Kompasla istiqamət müəyyənləşdirəndə, xəritədə məsafə ölçəndə, körpü konstruksiyasını hesablayanda və ya sadəcə bir dairəni bərabər hissələrə böləndə hamımız bu anlayışdan yararlanırıq. Qövsün dərəcə ölçüsü dairə boyunca hərəkəti, fırlanmanı və bucaqları kəmiyyətcə ifadə etməyi mümkün edir. Ümumi qəbul olunmuş 360° sistemi qədim astronomların göy sferasını müşahidələrindən doğsa da, bu gün həm elmi tədqiqatların, həm də mühəndis tətbiqlərinin bünövrə daşına çevrilib. Dərəcə ölçüsü həm intuitivdir, həm də praktiki: tam çevrənin 360 bərabər hissəyə ayrılması günün saatlarına, ilin günlərinə və qədim altmışlıq say sisteminə uyğun gəlir. Bu struktur təbiətdəki təkrarlanan hadisələri hesablamağa, kosmosda cisimlərin trayektoriyasını modelləşdirməyə və texniki çertyojları dəqiqliklə çəkməyə imkan verir. Riyaziyyat dərsliklərində qövsün dərəcə ölçüsünü radian, grad və ya çevrə faizi kimi alternativ sistemlərlə müqayisə edərkən, tələbələr fəza təsəvvürünü genişləndirir və nisbət anlayışlarını möhkəmləndirirlər. Hər bir dərəcə kəsiyi müəyyən uzunluqdakı qövs parçalarına uyğun gəlir və bu əlaqə geometriyanın məlumat bazasında sabit qalır. Qövs ölçüsünün gündəlik həyata nüfuz etməsi sürücülərin döngələrdə istiqamət dəyişməsindən tutmuş aviasiyada kurs bucaqlarının hesablanmasına qədər özünü göstərir. Elmi termin kimi sadə görünən bu anlayış, əslində, sivilizasiyanın ritmini, mühəndis qurğuların etibarlılığını və texnologiyanın dəqiqliyini təmin edən sütun rolunu oynayır. Qövsün dərəcə ölçüsünü dərindən dərk etmək həm riyaziyyat sevərlər üçün intellektual həyəcan, həm də praktik peşələr üçün vazkeçilməz alətdir.
Qövsün Tərifi Və Tarixi İnkişafı
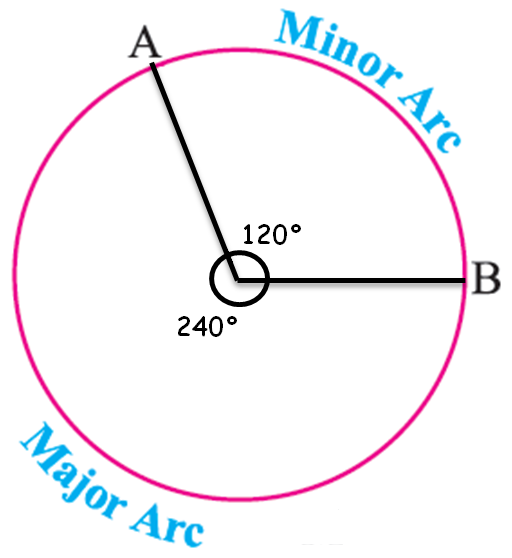
Qövs dairənin iki nöqtəsini birləşdirən əyridir və bu əyrinin uzunluğu dairə radiusu ilə əlaqədə ölçülür. Antik Mesopotamiya riyaziyyatçıları göy sferasını öyrənərkən tam çevrəni 360 bərabər hissəyə ayıraraq hər hissəni bir dərəcə adlandırdılar. Bu seçim ilin təqribən 360 gün hesab edilməsindən və altmışlıq say sistemindən qaynaqlanırdı. Beləcə, bir dərəcə dairənin 1/360 hissəsinə uyğun gəldi.
Orta əsr ərəb və Hindistan alimləri dərəcə ölçüsünü geniş astronomik cədvəllərə tətbiq etdilər və sinus funksiyasını tərtib etdilər. XV əsrdə Avropa riyaziyyatçıları trigonometriya terminlərini latın dilinə uyğunlaşdırarkən bu sistemin bütün Qərb elmlərini əhatə etməsinə zəmin yaratdılar. Nəticədə dərəcə anlayışı göy xəritələrinin, dənizçilik almanaxlarının və topoqrafik planların dilinə çevrildi.
Dərəcə Ölçüsünün Riyazi Əsasları
Dairənin mərkəzindən çəkilən şüalar döndükcə yaranan bucaq dərəcə ilə ifadə olunur; 360° tam dövrədir. Bir dərəcə 60 artıq dəqiqəyə, hər dəqiqə isə 60 artıq saniyəyə bölünür. Bu bölünmə fəzada çox incə bucaqları belə dəqiqliklə təsvir etməyə imkan verir. Planetlərin optik müşahidələrində saniyə kəsiyi vacib rol oynayır.
Dərəcə ölçüsünü radianla müqayisə edərkən 180°-nin π radian olduğu qəbul edilir. Beləliklə, 1° ≈ π/180 rad. Radian anlayışı diferensial hesablamalarda üstünlük təşkil etsə də, sadə konstruksiya və praktiki bucaq ölçmələrində dərəcə son dərəcə rahatdır. Riyaziyyat dərslərində iki sistemin çevrilməsi tələbələrə nisbətlərin məntiqini dərin öyrədir.
Qövs Uzunluğu İlə Dərəcə Ölçüsü Arasındakı Əlaqə
Eyni radiuslu dairələrdə eyni dərəcə ölçüsünə malik qövs parçalarının uzunluqları eynidir. Qövs uzunluğu S formula S = (π·R·α)/180 ilə hesablanır; burada R – radius, α – dərəcədir. Dərəcə artdıqca qövsün uzunluğu birbaşa proporsional şəkildə artır və yarım çevrədə α=180° bərabərdir πR-yə.
Bu nisbət arxitektur konstruksiyaların, körpü tağlarının və dairəvi rels döngələrinin planlaşdırılmasında vacibdir. Mühəndislər radiusu məlum olan dairədə konkret uzunluqda tağ yaratmaq üçün dərəcəni ilkin parametr kimi istifadə edirlər. Hətta avtomobil yollarında dönmə radiusu tənzimlənərkən də bu qaydaya əsaslanılır.
Trigonometriyada Qövsün Dərəcə Ölçüsü
Sinus, kosinus və tangent funksiyaları dairənin mərkəzindəki bucaqla düz əlaqəlidir. Bu bucaq dərəcə ilə ifadə olunduqda vahid çevrə diaqramı üzərində vizual interpretasiya asanlaşır. Trigonometriya cədvəllərində 0°-dən 90°-yə qədər funksion dəyərlər qədim dövrlərdən əllə hesablanaraq tərtib olunmuşdur.
Cəbrlə trigonometriyanın sintezi məhz dərəcə ölçüsünün sayəsində quadrat tənliklər şəklində praktiki məsələləri həll etməyə imkan verdi. Məsələn, bina hündürlüyünü ölçmək üçün bucağın dərəcə ölçüsü ilə tangent nisbəti kifayətdir. Radian sistemində eyni hesablama mümkün olsa da, gündəlik alətlər dərəcə sistemini daha əlçatan edir.
Geodeziyada Və Xəritəçəkmədə Tətbiqlər
Yer səthinin ölçülməsi üçün geodeziya elmində bucaqların dəqiq müəyyən edilməsi vacibdir. Teodolit və taximetr kimi cihazlar dərəcə, dəqiqə, saniyə oxunuşu üzrə kalibrlənir. Üfüqdə iki nöqtə arasındakı bucaq müəyyən edildikdən sonra üçbucaqlandırma üsulu ilə məsafələr hesablanır.
Xəritəçəkmə zamanı meridian və paralel şəbəkələri dərəcə intervalları ilə çəkilir. GPS sistemləri də Yer elliptik koordinatlarını dərəcə, dəqiqə, saniyə şəklində verir. Mühəndislik layihələrində plan və profil rəsmlərində torpaq hissələrinin bucağı bu ölçü vahidi ilə qeyd olunduğuna görə dərəcə geodeziyanın universal dili kimi qəbul edilir.
Fizikada Qövs Ölçüsünün İstifadə Sahələri
Fizikada fırlanma hərəkəti, dalğaların interferensiyası və maqnit sahələrinin istiqaməti kimi anlayışlar bucaqlarla sıx bağlıdır. Klassik mexanikada bərk cismin dönməsi zamanı keçilən bucaq dərəcə ilə ölçülür; zamanla bölündükdə isə bucaq sürəti alınır. Eksperimental cihazların, məsələn, difraksiya spektrometrlərinin şkala oxunuşu dərəcədir.
Optikada linzaların fokus bucaqları və prizmalardakı aşma bucaqları da dərəcə ilə qeyd edilir. Elektrik mühəndisliyində fəzə bucağı, alternativ cərəyanın fazalararası dərəcəsi enerji paylama sxemlərinin əsas parametrlərindəndir. Bu səbəbdən dərəcə ölçüsü çoxsaylı fiziki formulların birbaşa elementidir.
Tədrisdə Qövs Ölçüsünün Öyrədilməsi Metodları
Məktəb proqramında bu mövzu başlanğıc geometriya bölməsində təqdim edilir. Müəllimlər kompasiya və bucaqölçəni istifadə edərək şagirdlərə dərəcənin vizual mahiyyətini göstərirlər. Dairəvi kağız modelini 360 bərabər sektoruna kəsib paylaşdırmaq şagirdlərdə tam çevrə anlayışını möhkəmləndirir.
Radian-dərəcə çevrilməsini başa düşmək üçün praktiki laboratoriya işi keçirilməsi tövsiyə olunur: fərqli radiuslu dairələrdə eyni açıda qövs uzunluqlarını ölçmək. İnteraktiv proqram təminatları və rəqəmsal lövhələr vasitəsilə animasiyalı fırlanma hərəkətləri nümayiş etdirilir. Beləcə, abstrakt terminlər konkret müşahidəyə çevrilir.
Rəqəmsal Texnologiyalarda Qövs Ölçüsü Hesablamaları
Müasir qrafik mühərriklərdə, CAD sistemlərində və üçölçülü modelləşdirmə proqramlarında bucaqların dərəcə və ya radian formatında daxil edilməsi seçilə bilir. Oyun dizaynında kamera fırlanması, robot texnikasında servo mühərriklərin döndüyü bucaq əksər vaxt dərəcə ilə proqramlaşdırılır.
GIS tətbiqlərində coğrafi koordinatların dərəcə formatında saxlanılması böyük həcmli məkan məlumatlarını vahid sistemdə birləşdirməyə şərait yaradır. Drone naviqasiyasında kurs bucaqları, tilt və pan parametrləri də eyni vahidlə verilir. Dərəcə ölçüsü alqoritmləri sadələşdirir, çünki 360 dövrə ədədi emal üçün rahat diapazondur.
| Dərəcə, Radian, Grad Qarşılaşdırılması | Əsas Uyğunluqlar |
|---|---|
| 360° = 2π rad ≈ 400 grad | Tam çevrə |
| 180° = π rad ≈ 200 grad | Yarım çevrə |
| 90° = π/2 rad ≈ 100 grad | Dörddəbir çevrə |
| 1° ≈ 0,017453 rad ≈ 1,111 grad | Ən kiçik vahid (dərəcə) |
| 1 rad ≈ 57,2958° ≈ 63,662 grad | Radian çevirmə əmsalı |
Qövsün dərəcə ölçüsü riyaziyyatın özəyində dayanan sadə, lakin çoxcəhətli anlayışdır. Antik dövrlərdə astronomik müşahidələr üçün yaradılmış bu sistem əsrlər ərzində mühəndislikdən informasiyaya qədər saysız sahələrin universal dilinə çevrildi. Hər bir dərəcə kəsiyi dairə boyunca sabit paylanma təmin edərək təbiətdəki ritmləri riyazi dəqiqliklə təsvir etməyə imkan verir. Geodeziyada bucaqların dəqiq ölçülməsi düzgün xəritələrin, sərhəd xəttinin və infrastruktur obyektlərinin layihələndirilməsinin vacib şərtidir. Fizikada fırlanma hərəkətinin, optik bucaqların və enerji fazalarının hesablanması məhz dərəcə vahidinə söykənir. Tədris prosesində bu mövzunu praktik fəaliyyətlərlə müşayiət etmək şagirdlərdə məkan təsəvvürünü gücləndirir və riyazi əlaqələrin vizual başa düşülməsini asanlaşdırır. Rəqəmsal dövrdə də bu anlayış aktuallığını tam saxlayır: qrafik proqramlar, robot mexanizmləri və coğrafi informasiya sistemləri bu vahid üzərində qurulur. Dərəcənin radian və grad kimi sistemlərlə çevik çevrilə bilməsi onun beynəlxalq elm və texnika mühitində universallığını artırır. Qövs ölçüsünün tətbiq sahələrinin genişliyi sivilizasiyanın hərəkət mexanizmi haqqında düşünəndə bu kiçik bucaq vahidinin nə qədər böyük rol oynadığını göstərir. Dairəvi hərəkət, fırlanma, təkrarlanma və harmoniyanın riyazi təmsilçisi olan dərəcə ölçüsü həm elmi, həm də praktiki problemlərin açarını təqdim edir. Bu bilik keçmişi bu günlə birləşdirərək gələcəyin texnoloji nailiyyətlərinə yol açır. Hər dəfə əlimizə bucaqölçəni götürüb dairəyə bölmə apararkən, əslində, min illər əvvəl formalaşmış bir mədəni irsi davam etdiririk. Qövsün dərəcə ölçüsü həyatın ritmini dəqiq rəqəmlərlə ifadə edən sadə, lakin əvəzsiz alətdir.
Ən Çox Verilən Suallar
Qövsün dərəcə ölçüsü dairənin 1/360 hissəsinə uyğun gələn bucaq ölçüsüdür. Başqa sözlə, tam çevrə 360° hesab edilir və qövs həmin çevrənin neçə dərəcəlik hissəsini tutur. Bu vahid antik dövrdə göy sferasını bölmək üçün seçilib, çünki 360 ədədi çoxlu bölənə malikdir. Bu gün də həm elmdə, həm də gündəlik ölçmələrdə istifadə olunur.
Qədim Babil astronomları altmışlıq say sistemindən istifadə edirdi və ilin 360 gün olduğu güman edilirdi. Bu ədədi həm altmışlıq sistemə, həm də il dövrünə uyğunlaşdırmaq asan idi. 360 ədədinin çoxlu böləni olması kiçik bucaqları rahat bölməyə şərait yaratdı. Sonrakı sivilizasiyalar bu praktik bölgünü saxlayaraq universal standart kimi qəbul etdilər.
Radian riyazi cəhətdən daha təməl bucaq vahididir: radius uzunluğundakı qövsə uyğun mərkəzi bucaq 1 rad hesab olunur. Tam çevrə 2π rad olduğuna görə 360°-yə bərabərdir. Deməli, 1° ≈ π/180 rad, əksinə 1 rad ≈ 57,2958°. Bu çevirmə riyazi və mühəndis hesablamalarında tez-tez tətbiq olunur.
Qövs uzunluğu S formul ilə tapılır: S = (π·R·α)/180, burada R radius, α isə qövsə uyğun dərəcədir. Məsələn, radiusu 10 m olan dairədə 45°-lik qövsün uzunluğu S = π·10·45/180 = 7,85 m təşkil edəcək. Bu nisbət körpü tağlarından rels döngələrinə qədər çoxlu praktiki məsələlərdə istifadə olunur.
Bir dərəcənin 60 dəqiqəyə, hər dəqiqənin 60 saniyəyə bölünməsi çox kiçik bucaqları ifadə etməyə imkan verir. Astronomiya və geodeziya kimi dəqiqlik tələb edən sahələrdə bu bölgü vacibdir. Planetlərin koordinatları, ulduz xəritələri və torpaq ölçüləri saniyə dəqiqliyində qeyd edilir. Bu sistem altmışlıq say sisteminin mirasıdır.
Geodeziya Yer səthinin ölçülməsi ilə məşğul olur və bucaqların dəqiq təyini həlledicidir. Teodolit və taximetr cihazları dərəcə, dəqiqə, saniyə oxunuşu üzrə kalibrlənir. Üfüqdə iki nöqtə arasındakı bucaq ölçülərək məsafələr üçbucaqlandırma ilə hesablanır. GPS koordinatları da dərəcə formatında verilir, bu isə qlobal uyğunlaşmanı təmin edir.
Fizikada fırlanma hərəkətinin analizi, optik bucaqlar, dalğa interferensiyası və alternativ cərəyan fazaları dərəcə ilə ifadə olunur. Bərk cismin bucaq sürəti dərəcə bölü saniyə vahidində hesablana bilər. Optik linzaların fokus bucaqları və prizmalardakı aşma bucaqları da dərəcə şəklində verilir. Bu vahid eksperimental cihazlarda tez-tez rast gəlinir.
Məktəblərdə kompas və bucaqölçü cihazları ilə praktik məşğələlər təşkil olunur. Şagirdlər dairəni 360 bərabər hissəyə bölməklə dərəcə anlayışını vizuallaşdırırlar. Radian-dərəcə çevrilməsi üçün laboratoriya işləri aparılır, bu da nisbət məntiqini möhkəmləndirir. İnteraktiv lövhələrdə animasiyalı fırlanma şəkilləri mövzunu əyaniləşdirir.
Qrafik mühərriklər, CAD sistemləri və dron naviqasiyası kimi tətbiqlərdə dərəcə formatı proqramlaşdırıcılar üçün intuitivdir. 360 diapazonu ədədi emal baxımından rahatdır və insan beynindəki dairə anlayışı ilə üst-üstə düşür. Kompüter oyunlarındakı kamera bucaqları, robot mexanizmlərində servo dönmələri dərəcə ilə parametrizə edilir. Bu, kodun oxunaqlığını artırır.
Radian riyazi baxımdan təməl vahid olsa da, dərəcə sistemi praktik asanlığı ilə seçilir. Əgər elmi və texniki standartlar tam radian formatına keçsə belə, gündəlik və tətbiqi sahələrdə dərəcədən imtina real görünmür. İnsan təfəkküründə 360 paylaşımının rahatlığı qalacaq. Buna görə gələcəkdə də iki vahid paralel işlək qalacaq.