Triqonometrik cədvəl riyaziyyatın ən qədim və ən praktik alətlərindən biridir; bu alət bucağı ədədi göstəriciyə, ədədi göstəricini isə real ölçüyə çevirən körpü rolunu oynayır. İstər geodeziya xəttində bir bucaqdan məsafə hesablamaq, istər memarlıqda yamacın meylini müəyyənləşdirmək, istərsə də fizikanın dalğa modellərində fazanı ölçmək lazım gəlsin, triqonometriya həmişə eyni dilda danışır. Cədvəl bu dilin sözlüyüdür: sin, cos, tan və digər funksiyaların tipik bucaqlar üçün qiymətləri toplu şəkildə əl altında olur. Hesablayıcılar və proqramlar dövründə belə, cədvəlin dəyəri itməyib; çünki o, yalnız rəqəm təqdim etmir, həm də funksiyaların davranışına dair intuisiyanı möhkəmləndirir. Məsələn, sin funksiyasının 0 ilə 90 dərəcə aralığında artan olması və cos funksiyasının eyni aralıqda azalan davranışı cədvəl sətirlərində aydın görünür. İnterpolasiya vərdişi – yəni, iki məhşur bucaq arasında qiyməti yaxınlaşdırmaq – cədvəllə işləyən hər kəsin təbii bacarığına çevrilir. Dərəcə və radian kimi vahidlərin çevrilməsində də cədvəlin başlığındakı sütunlar riyazi intizam yaradır. Tarix boyu bu cədvəllər xordlardan sinusa keçidi, dəqiqliyin 1 dərəcədən 1 dəqiqəyə, ordan da onluqlu dəqiqələrə enməsini təmsil edib. Bu gün müasir ölçü sistemləri, GPS və mühəndislik proqramları triqonometriyanın üzərində dayanır; cədvəl isə həmin sistemlərin “kağız üzərində” sadə modelidir. Yaxşı qurulmuş cədvəl səhv ehtimalını azaldır, sürətli qərarverməyə kömək edir və nəzəri anlayışlarla praktiki qiymətlər arasında dayanıqlı əlaqə yaradır.
Triqonometrik cədvəlin anlayışı və məqsədi
Triqonometrik cədvəl bucağın ölçüsünü giriş kimi qəbul edib sin, cos, tan, cot (lazım gəldikdə sec və csc) kimi funksiyaların çıxış qiymətlərini verən referans topludur. Ən sadə cədvəldə yalnız 0°, 30°, 45°, 60°, 90° kimi “əsas” bucaqlar yer alır; daha geniş cədvəllər isə bucağı 1°-lik, 0,1°-lik, hətta 1′ (dəqiqə) addımı ilə bölüb verirlər. Müasir dərsliklərin çoxunda dərəcə–radian qarşılığı da göstərilir ki, analitik hesablamaya keçid asanlaşsın. Hər sütun funksiyanın adını, hər sətir isə konkret bucağı ifadə etdiyindən, oxu istiqamətinin səhv götürülməsi kimi tipik xətaların qarşısı alınır.
Cədvəlin əsas məqsədi riyazi modeli ölçü alətinə çevirməkdir. Məsələn, yamac bucağı α (alfa) məlumdursa, sin α yamac boyunca düşey proyeksiyanı, cos α üfüqi proyeksiyanı, tan α isə düşey/üfüqi nisbəti göstərir. Bucağın özünü bir daha hesablamaq lazım deyil – cədvəl “hazır” funksional qiymət verir. Təcrübədə bu, ölçü cihazından və ya plan–sxemdən alınan bucağın real xətt ölçüsünə çevrilməsini xeyli sürətləndirir. Eyni prinsip optik triangulyasiyada, səs dalğası faza fərqlərində və elektrik mühəndisliyində də işləyir.
Tarixi inkişaf: xord cədvəllərindən sinusa
Triqonometrik cədvəlin kökləri antik dövrə gedir. Qədim yunan astronomları çevrə üzərində “xord” uzunluqlarını cədvəl şəklində toplayır, bucaqlarla xordlar arasında əlaqəni həmin topludan oxuyurdular. Daha sonra hind riyaziyyatçıları “yarım xord” modelini sistemləşdirərək onu “sinus” funksiyasına çevirdilər; bu addım cədvəlləri daha kompakt və istifadəyə yararlı etdi. İslam riyaziyyat məktəblərində sin və cos-la yanaşı tan və cot funksiyaları da praktikaya daxil oldu, bu isə müasir cədvəlin sütun strukturunu formalaşdırdı.
Orta əsrlərdə dəqiqlik tədricən artdı: əvvəlcə 1° addımı ilə verilən qiymətlər, sonra 30′ və 1′ addımı ilə zənginləşdi. Uluqbəyin Səmərqənd məktəbində hazırlanmış yüksək dəqiqlikli cədvəllər astronomiya müşahidələrini yeni mərhələyə daşıdı. Yeni dövrdə logaritmik cədvəllə triqonometrik cədvəlin birgə istifadəsi nəhəng hesablamaları əlverişli etdi; tabela, qayçı qaydası və interpolasiya vərdişi elmi–texniki çevikliyin simvoluna çevrildi. Bu xətt bugünkü rəqəmsal kalkulyatorların “arxa plan” fəlsəfəsidir.
Hesablama metodları və interpolasiya
Triqonometrik cədvəllər tarixən iki yanaşma ilə qurulub: dəqiq (yəni, riyazi cəhətdən sərt) seriya və ya çevirmələr, və təcrübə əsaslı yaxınlaşdırmalar. Seriya metodunda sin və cos Maclaurin–Taylor sıraları ilə hesablanır; kifayət qədər termin götürüləndə dəqiqlik artır. Tan və cot qiymətləri isə ya ayrıca seriya, ya da sin/cos nisbətindən hesablanır. Bu cür cədvəllərdə hər bucaq üçün səhv həddi ayrıca qiymətləndirilir və ümumiyyətlə, mötədil bucaqlarda çox toxunulmaz dəqiqlik əldə edilir.
Interpolasiya kiçik addımlı cədvəldə olmayan bucaqlar üçün qiyməti yaxınlaşdırma texnikasıdır. Ən sadə üsul xətti interpolasiyadır: iki yaxın bucağın dəyərləri arasında proporsiya qurulur. Məsələn, 37° üçün sin dəyəri 36° və 38° sətirlərinin arasında xətti çəkidə tapıla bilər. Daha dəqiq yanaşmalar – Lagrange interpolasiyası və ya fərqlər cədvəli – çoxbucaqlı polinomlar qurur və yuvarlaqlaşdırma səhvlərini aşağı salır. Praktikada 0,1° addımı və ya 1′ addımı ilə qurulan cədvəllərdə xətti interpolasiya çox vaxt kifayət edir.
Vahidlər: dərəcə, radian, qrad və çevirmə
Triqonometriyanın dili yalnız dərəcə ilə məhdudlaşmır. Radian bucağın “qövs/yarıçap” nisbəti kimi təbii vahididir; π radian 180°-yə bərabərdir, deməli 1 radian ≈ 57,2958°. Mühəndislik və ali riyaziyyatda analitik ifadələr, diferensial tənliklər və inteqral hesab üçün radian zəruri olur. Qrad (gon) isə çevrənin 400 bərabər hissəyə bölünməsi ilə alınan vahiddir; 100g = 90° deməkdir və bəzi geodeziya sistemlərində işlədilir.
Çevirmə formulları sadədir: dərəcə → radian üçün α(rad) = α(°) × π/180, radian → dərəcə üçün α(°) = α(rad) × 180/π. Dərəcə–dəqiqə–saniyə formatında isə 1° = 60′ və 1′ = 60″ olduğundan, 35°20′30″ = 35 + 20/60 + 30/3600 dərəcə kimi onluğa çevrilir. Cədvəldə bu çevirmələr başlıq və ya qeyd hissəsində verildikdə, oxucu vahidlər arasında itmir, hesabın ardıcıllığını qoruyur.
Cədvəl quruluşu və istifadədə tipik səhvlər
Yaxşı triqonometrik cədvəl başlıqlarda vahidi (° və ya rad), sətirdə bucağı, sütunlarda isə funksiyaları göstərir. Cədvəlin kənarında dərəcə, yuxarı sətirdə dəqiqə və ya dərəcənin onluq hissəsi verildikdə, oxu “koordinat” prinsipi ilə aparılır: kənar–yuxarı kəsişmədən düzgün hüceyrə seçilir. Nəticənin işarəsi və dərəcə kvadrantı nəzərə alınmalıdır: I kvadrantda sin və cos müsbət, II-də sin müsbət cos mənfi, III-də hər ikisi mənfi, IV-də sin mənfi cos müsbətdir.
Tipik səhvlərdən biri tan və cot üçün asimptotlara (90°, 270° və s.) yaxın bucaqlarda rəqəmləri səhv oxumaqdır. Tan 89° kimi bucaqlarda qiymət çox böyükdür; cədvəldə bu, ya xüsusi qeyd, ya da “müəyyən deyil” ifadəsi ilə verilir. İkinci tipik səhv yuvarlaqlaşdırmadır: ardıcıl iki əməliyyatda iki dəfə yuvarlaqlaşdırmaq səhvi böyüdür. Üçüncü səhv vahid qarışıqlığıdır: dərəcə ilə radianı qarışdırmaq yüksək dəqiqlik tələb edən işlərdə ciddi yanlışa səbəb olur.
Müasir tətbiqlər: təhsil, geodeziya, mühəndislik
Təhsil mühitində triqonometrik cədvəl funksiyaların qrafik davranışını “rəqəmləşdirir”. Şagird və tələbə cədvələ baxaraq hansı aralıqda hansı funksiyanın artdığını, sıfırdan keçdiyini, maksimum və minimuma yaxınlaşdığını fəhmlə görür. İnterpolasiya ilə cədvəl arasında dolaşıq münasibət qurmaq əvəzinə, sadə nümunələr – məsələn, 33°-ün sinini 30° və 36° arasından yaxınlaşdırmaq – yeyin öyrənməyə gətirib çıxarır. Bu, həm də xəta anlayışını praktikaya köçürür.
Geodeziyada trayektoriyanın bucaq–məsafə tarazlığı (triangulyasiya) triqonometriyanın gündəlik işidir. Bir baza xətti və iki bucaqdan çıxışla koordinatlar bərpa edilir; sahədə sürətli yaxınlaşdırmalar üçün cədvəl faydalıdır. Mexanika və tikinti mühəndisliyində yamac bucağı, qüvvə komponentləri və vibrasiya fazaları sin/cos hesabına ayrılır; cədvəl bu “ayırma”nın tez referansıdır. Elektrik mühəndisliyində faza bucaqları, güc üçbucağı və harmoniklər eyni dilə tərcümə olunur.
Riyazi xassələr: simmetriya və identiklər
Cədvəllə işləyərkən triqonometrik identiklər “yoxlama düsturu” rolunu oynayır. Ən fundamentalı sin²α + cos²α = 1 bərabərliyidir; cədvəldən oxunan iki qiymətin kvadratları toplanıb 1-ə yaxın gəlmirsə, oxuda və ya yuvarlaqlaşdırmada problem var. Digər faydalı əlaqə tan α = sin α / cos α və cot α = cos α / sin α düsturlarıdır; beləliklə, cədvəldə sütunlar arasında daxili uyğunlaşma qurulur. “Tamamlayıcı bucaqlar” qaydası da praktik yoxlamadır: sin(90° − α) = cos α, cos(90° − α) = sin α.
Simmetriya qaydaları işarə nəzarəti üçün əlverişlidir. Məsələn, sin(−α) = −sin α, cos(−α) = cos α; bu, funksiyanın cüt və ya tək olmasını göstərir. Toplama düsturları – sin(a±b), cos(a±b) – cədvəldə olmayan bucaqları iki tanış bucağın cəmi kimi yazıb hesablamağa imkan verir. Bu üsul interpolasiya ilə birlikdə cədvəli daha çevik iş alətinə çevirir.
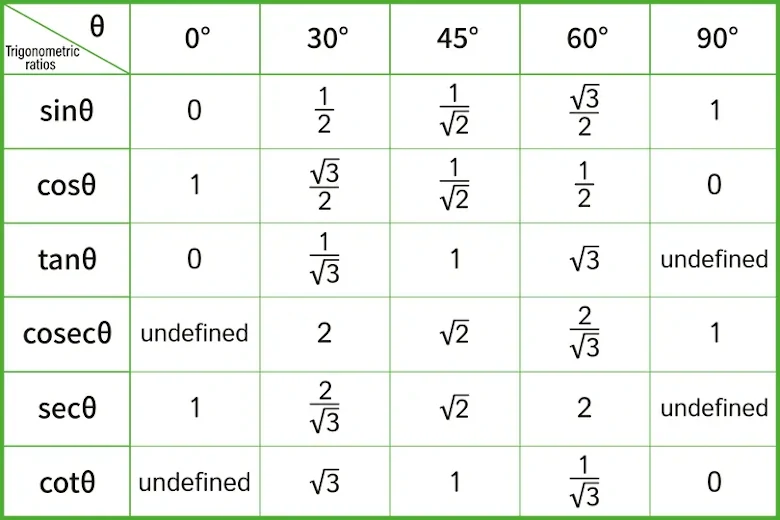
Kiçik istinad cədvəli: əsas bucaqlar üçün dəyərlər
Əsas bucaqlar üçün dəyərlər həm yadda saxlamaq, həm də sürətli yoxlama üçün uyğundur. 30°, 45° və 60° bucaqlarında sin və cos qiymətləri kvadrat köklərlə ifadə olunur: sin 30° = 1/2, sin 45° = √2/2, sin 60° = √3/2; cos bucaqları isə uyğun olaraq √3/2, √2/2 və 1/2 şəklində simmetriya göstərir. Tan 45° = 1 olduğu üçün yamac və proyeksiya məsələlərində bu bucaq “balans xətti” sayılır. 0° və 90° üçün sin/cos sərhəd qiymətləri funksiyanın aralıqdakı davranışını intuitiv edir.
Aşağıdakı kiçik cədvəl dərəcə və radian vahidlərində ən çox işlənən bucaqların sin, cos, tan və cot qiymətlərini xatırlatmaq üçün verilir. “Müəyyən deyil” qeydini tan 90° və cot 0°-da görməyiniz səbəbsiz deyil: bu nöqtələrdə funksiyanın məxrəci sıfıra yaxınlaşır və qiymət sonsuzluğa diverqsiya edir.
Triqonometrik istinad cədvəli (əsas bucaqlar)
| Bucağ (°) | Bucağ (rad) | sin | cos | tan | cot |
|---|---|---|---|---|---|
| 0° | 0 | 0 | 1 | 0 | müəyyən deyil |
| 30° | π/6 | 1/2 | √3/2 | 1/√3 | √3 |
| 45° | π/4 | √2/2 | √2/2 | 1 | 1 |
| 60° | π/3 | √3/2 | 1/2 | √3 | 1/√3 |
| 90° | π/2 | 1 | 0 | müəyyən deyil | 0 |
Triqonometrik cədvəl riyazi model ilə ölçü praktikası arasında ən etibarlı körpülərdən biridir. Cədvələ baxış funksiyaların qrafiklərini, artım–azalma zonalarını və işarə qaydalarını “rəqəmlə düşünmə” vərdişinə çevirir. Dərəcə–radian çevirmələri başlıqda görüldükcə, analitik formullarla əməli hesab arasında keçid asanlaşır. İnterpolasiya alqoritmi təxmini olsa da, kiçik addımlı cədvəldə onun xətası idarəolunandır; düzgün yuvarlaqlaşdırma bu xəttə intizam gətirir. Tarixi inkişafı – xorddan sinusa, dəqiqədən onluq dəqiqliyinə – riyaziyyatın mühəndisliklə necə sintez olunduğunu göstərir. Müasir cihazlar saniyələr içində funksion qiymətini versə də, cədvəl “niyə belədir?” sualını cavablandıran şəffaf pəncərədir. Təhsil mühitində o, anlayışların sadəcə əzbər deyil, əlaqə şəbəkəsi kimi mənimsənməsinə xidmət edir. Geodeziya və memarlıqdan elektronika və siqnallara qədər geniş tətbiq xətti cədvəlin həyatiliyi ilə izah olunur. İşarə qaydaları və identiklər isə cədvəldən oxunan rəqəmin öz-özünü yoxlamasına yardım edir. Sonda qalır peşəkar vərdiş: vahidi səhv salmamaq, asimptotlara yaxın bucaqlarda ehtiyatlı olmaq və iki dəfə yuvarlaqlaşdırmamaq. Bu intizam cədvəli sadə kağız cədvəldən etibarlı qərar alətinə çevirir. Öz-özünə yoxlama qaydalarını gündəlik praktikaya qatdıqda, triqonometrik cədvəl həm sürət, həm də dəqiqlik qazandırır.
Ən Çox Verilən Suallar
Triqonometrik cədvəl bucaqlar üçün sin, cos, tan və digər funksiyaların hazır qiymətlərini toplu şəkildə təqdim edən referansdır. O, bucağı xətt ölçüsünə, hündürlüyə və ya proyeksiyaya çevirmək üçün praktik alətdir. Təhsil, geodeziya, memarlıq və mühəndislikdə gündəlik hesabları sürətləndirir. Kalkulyator olsa belə, cədvəl funksiyanın davranışını vizual görməyə kömək edir.
Radian təbii bucaq vahididir və π rad = 180°-dir. Çevirmə üçün α(rad) = α(°) × π/180, əksinə α(°) = α(rad) × 180/π düsturundan istifadə edilir. Dərəcə–dəqiqə–saniyə formatı onluğa çevrilərək tətbiq olunur. Vahidlərin qarışdırılması böyük xətalara yol aça bildiyindən başlıqdakı vahidi yoxlamaq vacibdir.
Interpolasiya cədvəldə olmayan bucaq üçün iki yaxın bucağın dəyərləri arasında yaxınlaşdırmadır. Xətti interpolasiya kiçik addımlı cədvəllərdə (0,1° və ya 1′) adətən kifayətdir. Daha dəqiq nəticə üçün Lagrange interpolasiyası və ya fərqlər cədvəlindən istifadə olunur. Praktikada məqsəd xəta həddini nəzarətdə saxlamaqdır.
Tan α = sin α/cos α olduğuna görə cos α = 0 olduqda tan α müəyyən deyil; bu, 90°, 270° kimi bucaqlarda baş verir. Eyni qayda ilə cot α = cos α/sin α üçün sin α = 0 nöqtələrində dəyər müəyyən deyil. Bu hallarda funksiya sonsuzluğa meyl edir və cədvəl bunu qeyd etməklə oxucunu xəbərdar edir. Hesablamada həmin bucaqlardan qaçmaq və ya limitlə işləmək lazımdır.
Ən çox rast gəlinən səhvlər sütun–sətir qarışdırmaq, kvadrantı nəzərə almamaq və vahidi səhv seçməkdir. Asimptotlara yaxın bucaqlarda (məsələn, 89°) tan/cot qiymətlərini yanlış oxumaq da yayğındır. İki dəfə yuvarlaqlaşdırma xətanı böyüdür: əvvəl bucağı, sonra funksiyanı sərt yuvarlaqlaşdırmaq olmaz. Hər nəticəni identiklərlə yoxlamaq səhv ehtimalını azaldır.
Ən fundamental əlaqə sin²α + cos²α = 1 şəklindədir. Bu bərabərlik cədvəldən oxunan qiymətlərin səhv–düz yoxlanması üçün sadə testdir. Bundan əlavə, sin(90°−α) = cos α və cos(90°−α) = sin α “tamamlayıcı bucaqlar” qaydasını göstərir. Tətbiq zamanı bu identiklər işarə və böyüklüyü nəzarətdə saxlayır.
Cədvəl funksiyaların davranışını bir baxışda göstərir və intuitiv öyrənməni gücləndirir. Sahə işlərində və imtahan şəraitində sürətli yaxınlaşdırma üçün kalkulyatordan daha çevik ola bilər. Həm də yuvarlaqlaşdırma və xəta anlayışını konkret rəqəmlərlə hiss etməyə imkan verir. Bu, riyazi düşüncəni möhkəmləndirən didaktik alətdir.
Tarixi olaraq sin və cos Maclaurin–Taylor sıraları ilə, tan və cot isə nisbətlər və ya ayrıca sıralarla hesablanıb. Dəqiqlik üçün çox termin götürülür, sonra yuvarlaqlaşdırma qaydasına uyğun kəsilir. Geniş cədvəllərdə interpolasiya və fərqlər cədvəli ilə ara qiymətlər hazırlanır. Müasir dövrdə bu proses kompüterdə avtomatlaşdırılır, amma prinsip eynidir.
Formul sadədir: dərəcə + dəqiqə/60 + saniyə/3600. Məsələn, 35°20′30″ = 35 + 20/60 + 30/3600 = 35,3417° (təxmini). Əks çevirmədə onluq hissəni 60-a vurub dəqiqə, qalanını yenə 60-a vurub saniyə alırsınız. Çevirmədən sonra cədvəldə uyğun sətir–sütun seçmək asanlaşır.
Tətbiq məqsədinə görə 3–5 onluq mərtəbə çox vaxt kifayətdir. Geodeziya və yüksək dəqiqlik tələb edən hesablarda əlavə mərtəbələr saxlanır, lakin yuvarlaqlaşdırma qaydası ardıcıl tətbiq olunmalıdır. İki mərhələli yuvarlaqlaşdırmadan qaçınmaq xətanı azaldır. Nəticəni identiklərlə yoxlamaq dəqiqliyi təmin edir.