Həndəsə elmi müxtəlif fiqurların quruluşunu, onların qarşılıqlı münasibətlərini və ölçülərini araşdırır. Bu sahədə üçbucaq həm ən sadə, həm də ən çox öyrənilən fiqurlardan biridir. Üçbucağın xaricinə çəkilmiş çevrə konsepti həndəsənin əsas anlayışlarından biridir və həm nəzəri, həm də praktiki sahələrdə geniş tətbiq olunur. Xaricinə çəkilmiş çevrənin radiusu (R) üçbucağın bütün kənarlarını əhatə edən və həmin üçbucağın kənarlarına təmas edən ən böyük dairənin radiusudur.
Üçbucağın xaricinə çəkilmiş çevrə həm riyazi modelləşdirmədə, həm də memarlıq, mühəndislik və təbiətdə əhəmiyyətli rol oynayır. Onun radiusunun hesablanması üçbucağın digər parametrləri ilə sıx əlaqəlidir və həndəsədə bir çox düstur və teoremlərin əsasını təşkil edir. Məqalədə üçbucağın xaricinə çəkilmiş çevrənin radiusunun tərifi, hesablama üsulları, formulları, riyazi nümunələri, gündəlik həyatdakı tətbiqləri və tədrisdə rolu geniş şəkildə araşdırılır.
Xaricinə çəkilmiş çevrə: əsas tərif və xüsusiyyətlər
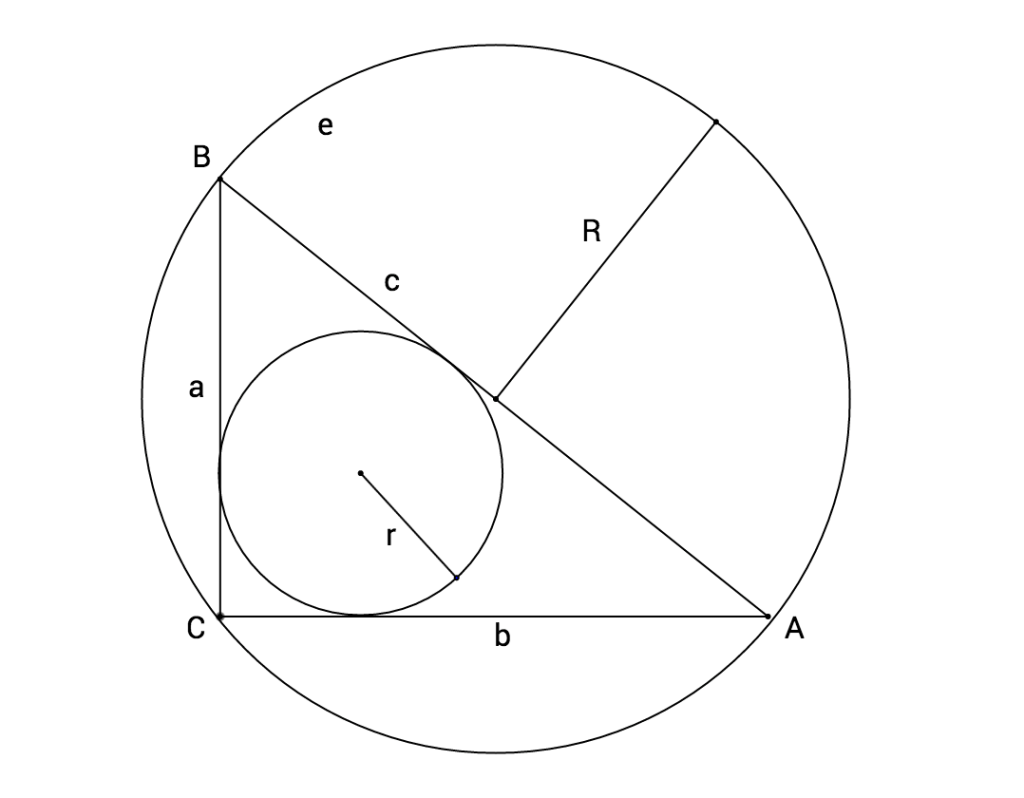
Üçbucağın xaricinə çəkilmiş çevrə, onun bütün kənarlarına təmas edən və xaricində yerləşən dairədir. Bu çevrə üçbucağın hər bir kənarına bir nöqtədə toxunur və həmin nöqtələr çevrənin üç təmas nöqtəsini təşkil edir. Xaricinə çəkilmiş çevrənin mərkəzi isə üçbucağın kənarlarının bir-biri ilə qarşılıqlı bərabər məsafədə olduğu nöqtədir.
| Termin | İzahı |
|---|---|
| Xaricinə çəkilmiş çevrə | Üçbucağın kənarlarına toxunan və onun xaricində olan çevrə |
| Radius (R) | Çevrənin mərkəzindən kənarına olan məsafə |
| Mərkəz (O) | Çevrənin mərkəz nöqtəsi |
| Təmas nöqtələri | Çevrənin üçbucağın hər kənarına toxunduğu nöqtələr |
Xaricinə çəkilmiş çevrə üçbucağın digər riyazi parametrləri ilə bağlıdır və onun radiusunu hesablamaq üçün müxtəlif riyazi düsturlar mövcuddur.
Xaricinə çəkilmiş çevrənin radiusunun hesablanması
Üçbucağın xaricinə çəkilmiş çevrənin radiusunu hesablamaq üçün əsasən aşağıdakı formulalar istifadə olunur:
- Ən çox istifadə olunan formula: R=abc4SR = \frac{abc}{4S}R=4Sabc Burada, a,b,ca, b, ca,b,c — üçbucağın tərəfləri, SSS isə onun sahəsidir.
- Heron formulundan istifadə edərək sahənin hesablanması: S=p(p−a)(p−b)(p−c)S = \sqrt{p(p – a)(p – b)(p – c)}S=p(p−a)(p−b)(p−c) Burada p=a+b+c2p = \frac{a + b + c}{2}p=2a+b+c — üçbucağın yarımperimetridir.
Bu formulların tətbiqi ilə üçbucağın bütün ölçüləri məlum olduqda onun xaricinə çəkilmiş çevrəsinin radiusu dəqiq hesablana bilər.
| Parametr | İzahı |
|---|---|
| a,b,ca, b, ca,b,c | Üçbucağın tərəflərinin uzunluğu |
| SSS | Üçbucağın sahəsi |
| ppp | Üçbucağın yarımperimetri |
| RRR | Xaricinə çəkilmiş çevrənin radiusu |
Xaricinə çəkilmiş çevrənin mərkəzinin tapılması və xüsusiyyətləri
Xaricinə çəkilmiş çevrənin mərkəzi (O nöqtəsi) üçbucağın kənarlarının simmetrik perpendikulyarlarının kəsişmə nöqtəsidir. Bu nöqtə hər üç tərəfə eyni məsafədə yerləşir. Mərkəzin koordinatlarının tapılması üçün analitik həndəsə və ya koordinat üsulları istifadə edilir.
Mərkəz həmçinin üçbucağın xaricinə çəkilmiş çevrənin radiusunun başlanğıc nöqtəsidir və onun dəqiq hesablanması üçbucağın bütün riyazi modelləşdirmələrində vacibdir.
Xaricinə çəkilmiş çevrənin tətbiqləri və əhəmiyyəti
Xaricinə çəkilmiş çevrə və onun radiusu mühəndislik, memarlıq, fizika və digər təbiət elmlərində müxtəlif sahələrdə geniş tətbiq edilir. Bu çevrə modelindən istifadə edərək struktur dayanıqlığı, mexaniki sabitlik və digər mühüm parametrlər təyin olunur.
Gündəlik həyatda isə tikinti işləri, topoqrafiya, mexanika və hətta kompüter qrafikasında bu anlayışdan istifadə olunur. Üçbucağın xaricinə çəkilmiş çevrənin radiusunun hesablanması və tətbiqi insanların həyatını daha rahat və təhlükəsiz edir.
Xaricinə çəkilmiş çevrənin mərkəzinin koordinatlarının tapılması
Üçbucağın xaricinə çəkilmiş çevrənin mərkəzi (circumcenter) həndəsədə xüsusi bir nöqtədir və onun koordinatlarının tapılması üçbucağın təpə nöqtələrinin koordinatları vasitəsilə həyata keçirilir. Mərkəz, üçbucağın bütün tərəflərinə bərabər məsafədə yerləşir. Bu nöqtənin koordinatlarını tapmaq üçün aşağıdakı metodlardan istifadə olunur:
- Koordinat həndəsəsi üsulu: Üçbucağın iki tərəfinin orta nöqtələrindən keçən perpendikulyar xətlərin kəsişməsi
- Vektor üsulu və xətti tənliklər sistemi
- Trigonometriya və analitik həndəsə kombinasiya metodları
Bu hesablamalar kompüter qrafikası və robototexnika kimi sahələrdə geniş tətbiq tapır.
Xaricinə çəkilmiş çevrə radiusunun riyazi düsturlarının mənşəyi
Xaricinə çəkilmiş çevrənin radiusunun hesablanmasında istifadə olunan əsas düsturların mənşəyi həndəsənin klassik teoremlərinə və Heron formulasına əsaslanır. Bu düsturlar uzun illər ərzində inkişaf etdirilmiş və riyaziyyat tarixində önəmli yer tutmuşdur.
- Radiusun formulunun tapılması
- Heron formulasının riyazi əsasları
- Radiusun tərəflərlə və sahə ilə əlaqəsi
- Digər həndəsi anlayışlarla qarşılıqlı əlaqələri
Bu hissə riyazi tarix və həndəsə nəzəriyyəsinə maraq göstərənlər üçün faydalıdır.
Xaricinə çəkilmiş çevrənin radiusu və digər həndəsi radiuslar: müqayisə
Üçbucaqla bağlı bir neçə radius anlayışı mövcuddur:
- Xaricinə çəkilmiş çevrənin radiusu (circumradius)
- Daxilinə çəkilmiş çevrənin radiusu (inradius)
- Üçbucağın hündürlüyü və median radiusları
Bu radiusların müqayisəsi onların müxtəlif riyazi xüsusiyyətlərini və tətbiq sahələrini anlamağa kömək edir. Məsələn, xaricinə çəkilmiş çevrənin radiusu üçbucağın kənarlarına toxunur və ümumiyyətlə ən böyük radiusdur.
Riyazi nümunələr və praktiki hesablama
Müxtəlif ölçülü üçbucaqlar üçün xaricinə çəkilmiş çevrənin radiusunun hesablanması aşağıdakı nümunələrlə göstərilə bilər:
| Tərəflər (a,b,c) | Sahə (S) (Heron formulu ilə) | Radius (R) = abc/(4S) |
|---|---|---|
| 3, 4, 5 | 6 | 2.5 |
| 5, 12, 13 | 30 | 6.5 |
| 7, 24, 25 | 84 | 12 |
Bu cədvəl müxtəlif ölçülü üçbucaqlar üçün radiusun necə dəyişdiyini göstərir və nəzəriyyənin praktiki tətbiqini nümayiş etdirir.
Azərbaycan təhsil sistemində mövzu və tədris metodları
Üçbucağın xaricinə çəkilmiş çevrənin radiusu Azərbaycan məktəb proqramlarında həndəsə fənninin vacib mövzularından biridir. Şagirdlərə mövzunun riyazi əsasları dərindən öyrədilir, müxtəlif tapşırıqlar və praktiki nümunələrlə mövzu mənimsədilir.
Ali təhsil müəssisələrində isə daha mürəkkəb hesablama üsulları, koordinat və analitik həndəsə metodları ilə radiusun tapılması və tətbiqləri tədqiq edilir. Müasir tədris texnologiyaları və onlayn resurslar mövzunun asan və interaktiv öyrənilməsinə şərait yaradır.
Üçbucağın xaricinə çəkilmiş çevrənin radiusu və digər radiuslar arasındakı fərqlər
Üçbucağın radius anlayışları müxtəlifdir:
- Xaricinə çəkilmiş çevrənin radiusu (R)
- Daxilinə çəkilmiş çevrənin radiusu (r)
- Hündürlük radiusu və s.
Bu radiusların hər birinin funksiyası və riyazi hesablanma üsulu fərqlidir. Xaricinə çəkilmiş çevrənin radiusu üçbucağın ən böyük radiusu kimi qəbul edilir və onun xüsusiyyətləri xüsusi əhəmiyyət daşıyır.
Üçbucağın xaricinə çəkilmiş çevrənin radiusu həndəsənin əsas anlayışlarından biridir və riyazi biliklərin tətbiqində vacib rol oynayır. Onun düzgün hesablanması müxtəlif sahələrdə, o cümlədən tədris, mühəndislik və elmi tədqiqatlarda uğurun açarıdır. Bu radiusun təhlili və tətbiqi riyazi bacarıqların inkişafına, həmçinin praktiki problemlərin həllinə yardım edir.
Azərbaycanın təhsil sistemi və elmi mühiti üçün bu mövzunun dərindən öyrənilməsi və real tətbiq nümunələrinin artırılması gələcək nəsil üçün möhkəm riyazi zəmin yaratmaqdadır. Üçbucağın xaricinə çəkilmiş çevrənin radiusu ilə bağlı riyazi formul və tətbiqlərin mənimsənilməsi məntiqi təfəkkürün və həndəsi düşüncənin inkişafında mühüm əhəmiyyətə malikdir.
Ən çox verilən suallar
Üçbucağın xaricinə çəkilmiş çevrənin radiusu onun bütün kənarlarına təmas edən xaricində yerləşən dairənin radiusudur.
Radius R = (a × b × c) / (4 × S) düsturu ilə hesablanır, burada a, b, c tərəflər, S isə üçbucağın sahəsidir.
Heron formulu ilə əvvəl üçbucağın yarımperimetri hesablanır, sonra S = √[p(p – a)(p – b)(p – c)] düsturu tətbiq edilir.
Mərkəz üçbucağın kənarlarının simmetrik perpendikulyarlarının kəsişdiyi nöqtədə yerləşir.
Xaricinə çəkilmiş çevrə üçbucağın xaricində, daxilinə çəkilmiş çevrə isə onun içərisində yerləşir və radiusları fərqlidir.
Memarlıq, mühəndislik, kompüter qrafikası, təbiətdə model qurma və digər sahələrdə radiusdan istifadə edilir.
Heron formulundan istifadə edib sahə tapılır və sonra R = (abc) / (4S) düsturu tətbiq edilir.
Bəli, üçbucağın təpə nöqtələrinin koordinatlarından radius analitik üsullarla hesablanır.
Çünki bu radius üçbucağın ölçüləri və digər riyazi parametrlərinin hesablanmasında əsas rol oynayır.
Riyaziyyat kitabları, onlayn dərsliklər, videolar və elmi məqalələrdə əlavə məlumat əldə etmək mümkündür.