Həndəsənin ən əsas və təməl çoxüzlü fiqurlarından biri üçbucaqlı piramidadır. Hər bir piramidanın konstruksiyasını, sabitliyini və həcm-məkan xüsusiyyətlərini müəyyən edən ən əsas elementlərdən biri də onun tilləridir. Riyaziyyatda və tətbiqi elmlərdə üçbucaqlı piramidanın tilləri, onların qarşılıqlı münasibətləri, uzunluqları, bucaqları və düzülüş prinsipləri yalnız nəzəri anlamda deyil, həm də praktiki həyatda xüsusi əhəmiyyət daşıyır. Tillər piramidanın həm dayanıqlığını, həm də xarici görkəmini müəyyən edir. Arxitektura, mühəndislik, texnologiya və təbiət elmlərində üçbucaqlı piramidanın məhz tilləri quruluşun mexaniki və vizual xarakteristikasını formalaşdırır.
Üçbucaqlı piramidanın tilləri haqqında dolğun, sistemli və təsdiqli biliklər həm məktəb riyaziyyatı, həm də ali təhsil səviyyəsində, müxtəlif fənlərin tədrisində mühüm yer tutur. Bu məqalədə üçbucaqlı piramidanın tillərinin həndəsi quruluşu, onların növləri, hesablanması, gündəlik həyatda və texnoloji proseslərdə tətbiqi, Azərbaycanın təhsil və elmi tədqiqatında rolu, tillərin ölçülərinin və aralarındakı münasibətlərin cədvəl və misallarla geniş izahı veriləcək. Məqalə həm akademik, həm də gündəlik istifadəçi üçün anlaşıqlı və maraqlı şəkildə tərtib olunub.
Üçbucaqlı piramidanın tilləri: əsas anlayışlar və tərifi
Üçbucaqlı piramidanın (tetraedr) tilləri dedikdə onun təpə nöqtələri arasında birbaşa birləşdirilən düz xətlər nəzərdə tutulur. Riyaziyyatda “till” termini əsasən “kənar” (və ya “rib”) kimi istifadə olunur və çoxüzlü fiqurların strukturunda ən önəmli həndəsi elementlərdən sayılır.
Üçbucaqlı piramidada ümumilikdə 6 till mövcuddur:
- Əsas üçbucağın 3 tilli (baza tərəfləri)
- Hər bir təpə nöqtədən əsasın üç nöqtəsinə çəkilən 3 yan till
Yəni:
| Tillin növü | Miqdarı | Həndəsi rolu |
|---|---|---|
| Əsasın tilləri | 3 | Piramidanın baza səthini təşkil edir |
| Yan tillər | 3 | Baza ilə zirvəni birləşdirir |
| Cəmi tillərin sayı | 6 | Piramidanı təşkil edən bütün kənarlar |
Bu tillərin hər birinin uzunluğu, bucaqları və aralarındakı məsafə piramidanın formasını, sabitliyini və həcmini müəyyən edir. Hər bir till iki təpə nöqtəsi arasında düz xəttdir və üçbucaqlı piramidanın əsas konstruksiya xəttini təşkil edir.
Tillərin riyazi xüsusiyyətləri və qarşılıqlı münasibətləri
Hər üçbucaqlı piramidada bütün tillərin bir-birinə olan münasibəti, uzunluqları və yerləşməsi həndəsənin fundamental məsələlərindəndir. Əgər piramida bərabərtərəfli və simmetrikdirsə, bütün tillərin uzunluğu eyni olur. Əks halda, fərqli uzunluqlu tillər fiqurun qeyri-müntəzəm formasını yaradır.
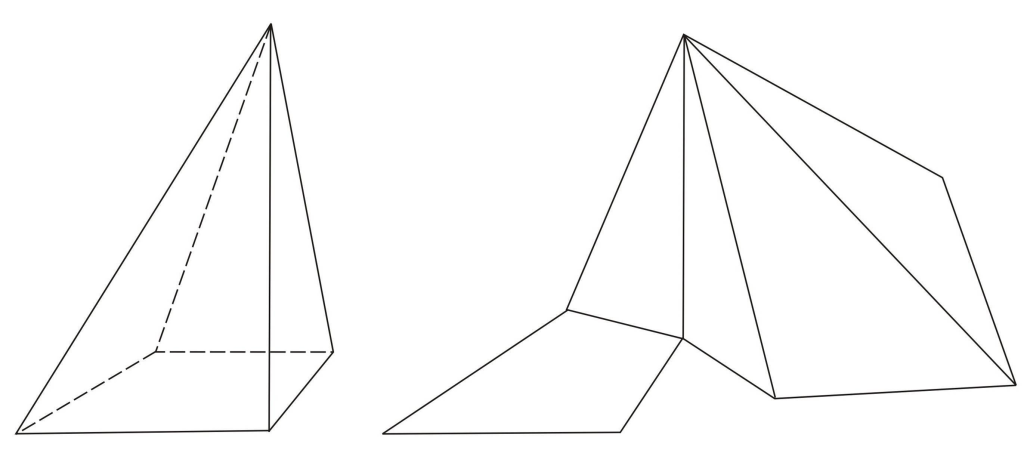
Əsas üçbucağın hər tərəfi bir till sayılır və bu tillər arasında yerləşən bucaqlar əsas üçbucağın daxili bucaqlarıdır. Yan tillər isə əsasın hər bir təpəsindən piramidanın zirvəsinə çəkilən düz xətlərdir.
Riyazi olaraq, istənilən iki till arasında bucaq tapmaq, bir tillin uzunluğunu digər tərəf və bucaqlarla ifadə etmək üçün həndəsi teorem və formulalardan istifadə edilir. Bu əlaqələr həm planimetriyada, həm də stereometriyada geniş istifadə olunur.
Tillərin uzunluqlarının hesablanması üsulları
Üçbucaqlı piramidanın hər bir tillinin uzunluğunu tapmaq üçün bir neçə riyazi üsul mövcuddur. Əgər piramidanın təpə nöqtələrinin koordinatları məlumdursa, aşağıdakı formula tətbiq edilir:
Tillin uzunluğu:
l = √[(x₂-x₁)² + (y₂-y₁)² + (z₂-z₁)²]
Əgər baza və yan tərəflərin uzunluqları məlumdursa, yan tillərin uzunluğunu üçbucağın Pifaqor teoremi və ya kosinüs teoremi vasitəsilə hesablamaq mümkündür. Simmetrik piramidalarda isə hər üç yan tillin uzunluğu və baza tərəfləri eyni olur.
Tillərin ölçüləri və aralarındakı məsafələrin düzgün hesablanması piramidanın səthinin, həcminin, daxili bucaqlarının və digər həndəsi parametrlərinin tapılması üçün əsasdır.
| Tillin növü | Hesablanma üsulu |
|---|---|
| Əsas tillər | Üçbucağın tərəfi kimi birbaşa verilir |
| Yan tillər | Koordinat üsulu, Pifaqor/Kosinüs teoremi |
Üçbucaqlı piramidanın tilləri və fiqurun sabitliyi
Piramidanın möhkəmliyi və sabitliyi məhz tillərin uzunluğundan və yerləşməsindən asılıdır. Bütün tillər bərabərdirsə, piramida maksimal dayanıqlılığa malik olur və simmetrik tetraedr adlanır. Bu cür piramidalar təbiətdə molekul modellərində, texnologiyada konstruktiv qurğularda, memarlıqda və müxtəlif mühəndislik sahələrində optimal enerji paylaşımı və sabitlik təmin edir.
Qeyri-müntəzəm piramidalarda isə tillərin uzunluğu fərqli olduqda fiqurun stabilliyi azala bilər. Buna görə, praktiki tətbiqlərdə tillərin ölçüləri və bucaqları xüsusi dəqiqliklə hesablanır və yoxlanılır.
Həndəsədə və tətbiqi elmdə üçbucaqlı piramidanın tillərinin rolu
Tillər yalnız nəzəri riyaziyyatda deyil, həm də tətbiqi elmdə – arxitektura, inşaat, avtomobil sənayesi, aviasiya və hətta kompüter qrafikasında fundamental rol oynayır. Üçbucaqlı piramidanın tilləri dayanıqlı skelet strukturları yaratmağa, böyük tikililərdə yükün bərabər bölüşməsinə, 3D modelləşdirmədə möhkəm konstruksiyaların qurulmasına imkan verir.
Məsələn, tetraedr modelində hər bir till digər iki till ilə sabit üçbucaqlı formalar yaradaraq fiqurun bütövlüyünü qoruyur. Bu, təbii və süni obyektlərin dayanıqlılığını artırır, texniki layihələrdə təhlükəsizlik və iqtisadi səmərəlilik yaradır.
Azərbaycanın təhsilində və elmi tədqiqatında piramida tilləri
Azərbaycanda üçbucaqlı piramidanın tilləri məktəb riyaziyyatında əsas mövzulardan biridir. Həm əsas, həm də yan tillərin təhlili, uzunluqların tapılması, fiqurun modelləşdirilməsi, tədris proqramlarında, olimpiada və test tapşırıqlarında geniş tətbiq olunur.
Universitet və elmi tədqiqatlarda isə piramida modellərinin kompüter proqramlaşdırılması, 3D dizayn, fiziki modelləşdirmə, materialşünaslıq və molekulyar kimyada praktiki nümunələr üzərində aparılır. Beləliklə, üçbucaqlı piramidanın tilləri Azərbaycan təhsil sistemində riyazi təfəkkürün, məkan təsəvvürünün və texniki yaradıcılığın formalaşmasında mühüm vasitədir.
Tillərin uzunluqları və münasibətlərinin cədvəli
Aşağıdakı cədvəldə üçbucaqlı piramidanın tillərinin növləri, riyazi ifadəsi və istifadə sahələri ümumiləşdirilib:
| Tillin növü | Riyazi ifadə və hesablanma | İstifadə sahəsi |
|---|---|---|
| Əsas tillər | a, b, c – baza üçbucağın tərəfləri | Piramidanın baza səthi |
| Yan tillər | d, e, f – zirvə ilə baza nöqtələri | Piramidanın yan səthləri |
| Koordinat tilləri | √[(x₂-x₁)²+(y₂-y₁)²+(z₂-z₁)²] | 3D modelləşdirmə, dizayn |
| Bərabər tillər | a = b = c = d = e = f | Simmetrik tetraedr |
| Fərqli tillər | Müxtəlif uzunluqlu tillər | Qeyri-müntəzəm piramida |
Tillərin gündəlik həyatda və texnologiyada tətbiqi
Gündəlik həyatda üçbucaqlı piramidanın tilləri müxtəlif texniki qurğuların, oyun modellərinin, dizayn və arxitektura elementlərinin əsas struktur xətti kimi çıxış edir. Çadır, sərgi pavilyonları, idman arenaları, həndəsi zərgərlik və aksesuarlar, habelə təbiətdə büllur və molekul formaları məhz tillərin bərabər və ya qeyri-bərabər paylanmasından yaranır.
Kompüter qrafikasında və proqramlaşdırmada isə üçbucaqlı piramidanın tilləri virtual fiqurların üçölçülü səhnələrdə modelləşdirilməsində baza strukturunu formalaşdırır. Texnoloji inkişafla yanaşı, bu elementlər süni intellekt, maşın öyrənməsi və robototexnikada da önəmli rol oynayır.
Üçbucaqlı piramidanın tilləri riyazi həndəsənin, texniki elmlərin və gündəlik həyatın əsas struktur elementlərindən biridir. Onların düzgün və dəqiq hesablanması piramidanın bütövlüyünü, sabitliyini, vizual gözəlliyini və texniki etibarlılığını təmin edir. Tillər məktəb proqramlarından başlayaraq mühəndislik, dizayn və elmi tədqiqat sahələrinə qədər geniş tətbiq imkanları yaradır. Hər bir istifadəçi üçün – istər şagird, istər müəllim, istər tədqiqatçı və ya memar – üçbucaqlı piramidanın tilləri həm fundamental bilik mənbəyi, həm də yaradıcılıq üçün sonsuz imkanlar açır.
Ən çox verilən suallar
Üçbucaqlı piramidanın ümumilikdə 6 tilli olur. Bunlardan 3-ü əsas üçbucağın tərəfləri, 3-ü isə təpə nöqtədən baza nöqtələrinə çəkilmiş yan tillərdir.
Tillin uzunluğu təpə nöqtələrinin koordinatları və ya baza tərəfləri məlum olduqda Pifaqor və ya kosinüs teoremi ilə hesablana bilər. Koordinat üsulu da tətbiq edilir.
Bərabərtərəfli piramidada bütün tillər eyni uzunluqdadır və piramida tam simmetrikdir. Qeyri-bərabər piramidada isə tillərin uzunluqları fərqlidir.
Memarlıq, mühəndislik, texnologiya, kompüter qrafikası, 3D modelləşdirmə, zərgərlik və texniki dizayn işlərində tillərin düzgün ölçülməsi və paylanması xüsusi əhəmiyyət daşıyır.
Çadır konstruksiyaları, sərgi pavilyonları, texnoloji qurğular, idman arenaları və həndəsi formalı zinət əşyalarında piramida tilləri geniş istifadə olunur.
Tetraedr ribləri və üçbucaqlı piramidanın tilləri eyni həndəsi elementlərdir, sadəcə fərqli terminlərdir.
Tillərin sayı və yerləşməsi fiqurun simmetriya və sabitliyinə birbaşa təsir edir. Bütün tillər bərabər olduqda piramida maksimal dayanıqlığa malik olur.
Tillin uzunluğunu hesablamaq üçün iki təpə nöqtəsinin koordinatları arasındakı fərqlərin kvadratları toplanır və kvadrat kökü alınır.
Məktəb proqramlarında tillərin uzunluqlarının tapılması, fiqurun sabitliyi, səth və həcmin hesablanması, modelləşdirmə və tətbiqi məsələlər geniş yer tutur.
Riyaziyyat dərslikləri, həndəsə kitabları, tədris videoları, elmi məqalələr və onlayn təhsil platformalarında üçbucaqlı piramidanın tilləri haqqında geniş məlumat tapmaq mümkündür.