Üçbucaqlı Prizma : Prizmanın Neçə Tili Var?

Riyaziyyatın və xüsusilə həndəsənin ən vacib sahələrindən biri üçölçülü fiqurların, yəni çoxüzlü bədənlərin öyrənilməsidir. Bu fiqurlar arasında üçbucaqlı prizma xüsusi yer tutur. Onun riyazi mahiyyəti, gündəlik həyatda tətbiqləri və nəzəri baxımdan həndəsi xüsusiyyətləri həm təhsildə, həm də elmi tədqiqatlarda geniş istifadə edilir. Üçbucaqlı prizma təməli üçbucaq olan, iki paralel və bərabər əsasdan və üç yan düzbucaqlı səthdən ibarət olan çoxüzlü fiqurdur. Prizmanın kənarları, üzü və təpələri arasındakı qarşılıqlı əlaqələr, eləcə də, neçə tili (kənarı) olması, riyaziyyatın əsas suallarından biridir.

Üçbucaqlı prizmanın tərifi və quruluşu

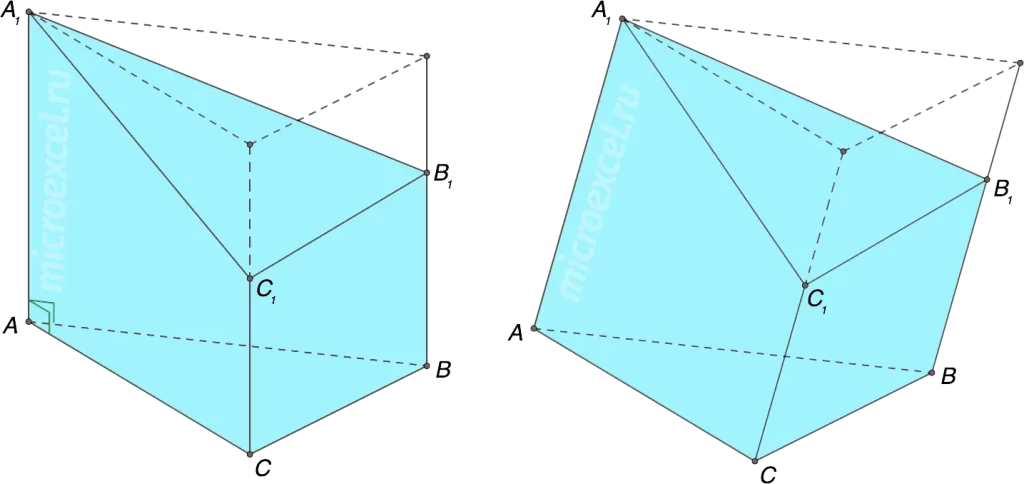
Üçbucaqlı prizma — təməlində və üstündə bərabər və paralel yerləşmiş iki üçbucaq olan, yan səthləri isə düzbucaqlardan ibarət olan çoxüzlü fiqurdur. Hər bir prizmanın ən azı üç əsas hissəsi olur: iki əsas (üst və alt üçbucaq) və yan səthlər (üç düzbucaqlı). Bu fiqurun bütün kənarları paralel olaraq və eyni uzunluqda yerləşir. Üçbucaqlı prizmada qarşı-qarşıya duran iki üçbucağın müvafiq tərəfləri bir-birinə bərabər və paralel olur. Yan səthlər isə həmin tərəfləri birləşdirən düzbucaqlardır. Bu baxımdan, üçbucaqlı prizmanın tam quruluşu həndəsi baxımdan çox maraqlıdır və öyrənilməsi bir çox fundamental riyazi biliklərə əsaslanır.

Tarixi və nəzəri baxış

Üçbucaqlı prizma, qədim Yunanistan və Roma riyaziyyatçıları tərəfindən öyrənilmiş, klassik həndəsənin əsas fiqurlarından biri kimi tanınmışdır. Euklid, Arximed və digər qədim alimlər prizmanın həcmini, səth sahəsini və digər xüsusiyyətlərini hesablamaq üçün riyazi düsturlar hazırlamışlar. Orta əsrlərdə isə prizmanın tətbiqi memarlıqda, mühəndislikdə və hətta bədii əsərlərdə də geniş yayılmışdır. Müasir dövrdə üçbucaqlı prizma kompüter qrafikası, 3D modelləşdirmə və texniki layihələndirmə sahələrində də əsas elementlərdən biri kimi qəbul olunur.

Prizmanın hissələri və əsas anlayışlar

Üçbucaqlı prizmada aşağıdakı hissələr mövcuddur:

• Əsaslar: İki bərabər və paralel üçbucaq (alt və üst).
• Yan səthlər: Üç düzbucaqlı.
• Kənarlar (tillər): Hər bir üçbucağın üç tərəfi və hər iki əsasın müvafiq nöqtələrini birləşdirən üç paralel kənar.
• Təpə nöqtələri: Altı təpə nöqtəsi (hər üçbucağın üç ucu).
  Hər bir yan səth müvafiq tərəfləri birləşdirən düzbucaqlı səthdir. Prizmanın simmetriyası, bərabərliyi və paralellik xüsusiyyətləri həndəsənin əsas tədqiqat obyektlərindəndir.

Üçbucaqlı prizmanın neçə tili (kənarı) var?

Ən əsas və tez-tez verilən suallardan biri budur: üçbucaqlı prizmanın neçə tili, yəni neçə kənarı var? Riyazi olaraq, üçbucaqlı prizmada doqquz tili (kənarı) olur:

• Hər üçbucağın (əsasların) üç tərəfi: 3 (alt) + 3 (üst) = 6
• Alt və üst əsasın müvafiq nöqtələrini birləşdirən üç paralel kənar: 3
  Beləliklə, ümumilikdə 6 + 3 = 9 tili (kənarı) var. Bu, bütün üçbucaqlı prizmalar üçün keçərlidir, istər bərabərtərəfli, istərsə də müxtəlif tərəfli olsun.

Üçbucaqlı prizmanın üzü və təpə nöqtələri

Prizmanın üzlərinin sayı altı olur: iki əsas (üçbucaqlar) və üç yan səth (düzbucaqlar). Təpə nöqtələrinin sayı isə altıdır – hər əsas üçbucağın üç nöqtəsi və onların paralel şəkildə birləşməsi nəticəsində altı unikal təpə nöqtəsi alınır. Üzlərin və təpələrin sayı həm riyazi həndəsə, həm də kompüter qrafikasında obyektin modelləşdirilməsi üçün əsas parametrdir.

Prizmanın həcmi və səth sahəsi

Üçbucaqlı prizmada həcmin tapılması üçün əsasın sahəsi ilə hündürlüyün hasilini hesablamaq lazımdır:
V = Səsas × hündürlük
Səth sahəsi isə bütün üzlərin sahələrinin cəminə bərabərdir:
S = 2 × Səsas + Syan səthlərin cəmi
Əgər əsas bərabərtərəfli üçbucaqdırsa, sahə və kənar uzunluqları üçün xüsusi düsturlardan istifadə edilir. Bu riyazi hesablamalar gündəlik həyatda və mühəndislikdə prizma formalı obyektlərin layihələndirilməsində mühüm rol oynayır.

Gündəlik həyatda və elmdə tətbiqləri

Üçbucaqlı prizmalar tikinti materiallarında, binaların dizaynında, optikada işıq prizması kimi, su boruları və bəzi texnoloji qurğuların əsas hissələrində geniş istifadə olunur. Kompüter oyunları və 3D modelləşdirmədə isə üçbucaqlı prizma elementar “mesh” strukturun qurulmasında əsas vahid rolunu oynayır. Təbiətdə bəzi kristallar və minerallar üçbucaqlı prizma formasında ola bilər. Eyni zamanda, müxtəlif memarlıq layihələrində və dizayn işlərində maraqlı konstruktiv həllər üçün bu fiqurdan geniş istifadə edilir.

Təhsil və riyazi düşüncənin inkişafında rolu

Azərbaycan məktəblərində və ali təhsil müəssisələrində üçbucaqlı prizmalar həndəsənin əsas bölmələrində öyrədilir. Riyazi düşüncənin, məkan təfəkkürünün inkişafı, analitik və konstruktiv bacarıqların formalaşmasında bu mövzu mühüm yer tutur. Prizmanın kəsikləri, həcminin və səthinin hesablanması, simmetriya və paralellik mövzularının praktiki tapşırıqlarda tətbiqi riyazi dünyagörüşü formalaşdırır. Bu, həmçinin, mühəndislik və texnologiya ixtisaslarında da əsas baza biliklərdəndir.

Kompüter qrafikası və modelləşdirmədə istifadəsi

Üçbucaqlı prizma 3D modelləşdirmədə və kompüter animasiyasında ən çox istifadə olunan əsas fiqurlardandır. Bu fiqurun quruluşu müxtəlif obyektlərin modelləşdirilməsi, səthin vizualizasiyası, işıqlandırma və kölgə effektlərinin yaradılmasında baza rolunu oynayır. Kompüter proqramlarında “mesh” strukturun təməl elementi olaraq, simulyasiya və dizayn işlərində çevik və dəqiq modellər yaratmağa imkan verir.

Mədəniyyət və incəsənətdə yeri

Tarix boyu üçbucaqlı prizmalar dekorativ sənətdə, bədii və texniki layihələrdə, hətta rəmzi mənalarda dayanıqlıq, tarazlıq və harmoniya simvolu kimi istifadə edilib. Müasir dizaynda və heykəltəraşlıqda bu fiqur həm estetik, həm də texniki üstünlükləri ilə seçilir. Eyni zamanda, bəzi binaların memarlıq planlarında və sənət əsərlərində üçbucaqlı prizmalar maraqlı kompozisiyalar yaradır.

Üçbucaqlı prizma həndəsənin ən maraqlı və əhəmiyyətli fiqurlarından biridir. Onun doqquz tili (kənarı), altı üzü və altı təpə nöqtəsi var. Prizmanın riyazi strukturu və praktiki tətbiqləri təhsil, elm, texnologiya və incəsənətdə geniş yer tutur. Hər bir üçbucaqlı prizmanın konstruksiyası, simmetriyası və həndəsi xüsusiyyətləri insanın məkan düşüncəsini və riyazi təfəkkürünü inkişaf etdirir. Gələcəkdə bu fiqurun daha innovativ və yaradıcı tətbiqləri müxtəlif sahələrdə əhəmiyyətini artıracaq.

Ən Çox Verilən Suallar