Riyaziyyatda məkan və forma anlayışı olmadan heç bir sistemli bilik, strukturlaşdırılmış yanaşma mümkün deyil. Həndəsi fiqurların quruluşu, onların hissələrə bölünməsi, analiz və tədqiqi əsrlər boyu alimlərin diqqət mərkəzində olub. Bu baxımdan “üz”, “til” və “təpə” anlayışları riyaziyyatın həndəsə və topologiya sahələrində, hətta qraf nəzəriyyəsində əsas elementlərdir. Hər bir fiqurun, poliedrin və ya qrafın strukturu bu üç element üzərində qurulur. İbtidai məktəbdən ali riyaziyyata qədər hər kəs bu terminlərlə rastlaşır, amma onların dərin məna qatını, tarixi inkişafını və müasir elmdəki rolunu çox zaman nəzərə almırıq. Bu sözlər elə bir kontekstdə işlədilir ki, onlar olmadan riyazi məkan təsəvvürünü tam, dəqiq və aydın ifadə etmək mümkün deyil.
Üz anlayışı: Riyaziyyatda və həndəsədə rolu
Üz riyaziyyatda çoxbucaqlı və çoxüzlü fiqurların ən əsas elementlərindən biri hesab olunur. Hər bir çoxüzlü – məsələn, kub, prizma, piramida və s. – məhz üzlərin məcmusundan formalaşır. Üz dedikdə fiqurun səthində yerləşən və iki ölçülü çoxbucaqlını təşkil edən düz hissə nəzərdə tutulur. Bu anlayış yalnız həndəsi formanın kənarları və təpələri ilə deyil, həm də məkanın necə bölündüyü, fiqurun necə görünməsi və onun səthi üzərində hansı əməliyyatların aparılacağı ilə sıx bağlıdır. Məsələn, kubun 6 üzü, piramidanın isə 5 üzü var. Hər bir üz fiqurun daxili və xarici xassələrini, eyni zamanda simmetriyasını və topoloji xüsusiyyətlərini müəyyən edir.
Üzlərin öyrənilməsi yalnız fiqurun ölçülərinin və formalarının deyil, həm də səthin sahəsinin, kəsiklərinin, bükülmələrinin və digər riyazi analizlərin aparılması üçün vacibdir. Riyazi modelləşdirmədə, riyazi fizika və həndəsədə üzlər bəzən sərhəd, bəzən də funksional səth rolunu oynayır. Poliedrlərin səthinin ölçülməsi, çoxüzlü fiqurların kompüter qrafikasında təsviri və real obyektlərin üçölçülü modelləşdirilməsi zamanı üzlər əsas baza rolunu oynayır.
Müxtəlif fiqurların üz, til və təpə sayı
| Fiqur | Üz sayı | Til sayı | Təpə sayı |
|---|---|---|---|
| Kub | 6 | 12 | 8 |
| Kvadrat prizma | 6 | 12 | 8 |
| Üçbucaq piramida | 4 | 6 | 4 |
| Düzgün onikibucaqlı | 12 | 30 | 20 |
| Düzgün altıbucaqlı prizma | 8 | 18 | 12 |
Til nədir və həndəsədə necə yaranır?
Til, həndəsə və riyaziyyatdakı ən əsas struktur elementlərdən biridir. Fiqurun iki üzü və ya iki səthi bir-biri ilə kəsişəndə meydana çıxan kənar, yəni düz xətt parçasına til deyilir. Başqa sözlə, til iki üzü birləşdirən və fiqurun konturunu, formalaşmasını təmin edən xətdir. Til olmadan çoxbucaqlının, poliedrin və ya prizmanın bütöv quruluşundan danışmaq mümkün deyil. Hər bir fiqurun til sayı onun üzləri və təpələri ilə birbaşa əlaqəlidir və riyaziyyatda ən fundamental tənliklərdən biri olan Eyler düsturunda da əsas rolu oynayır: Təpə sayı – Til sayı + Üz sayı = 2 (V – E + F = 2).
Tillin praktiki rolu, məsələn, qraf nəzəriyyəsində, üçölçülü modelləşdirmədə, memarlıq və konstruksiya layihələrində xüsusi önəm daşıyır. Məhz tilin uzunluğu, mövqeyi və birləşdiyi nöqtələr fiqurun dayanıqlığını və simmetriyasını müəyyən edir.
Təpə: Riyazi obyektlərin əsas dayaq nöqtəsi
Təpə (və ya düyün) riyaziyyatda fiqurun, qrafın, poliedrin və ya istənilən çoxölçülü obyektin əsas kəsişmə və birləşmə nöqtəsidir. Hər bir til iki təpəni birləşdirir, üzlər isə təpələr üzərində qapanır. Təpə nöqtəsi fiqurun formalaşmasında və məkan quruluşunun təsvirində fundamental əhəmiyyət daşıyır. Hər bir çoxbucaqlının, prizmanın və ya piramidanın təpələri onların konfiqurasiyasını və həndəsi xassələrini təyin edir.
Qraf nəzəriyyəsində təpə “vertex”, til isə “edge” adlanır. Burada təpələr istənilən əlaqələrin başlanğıc və son nöqtəsi olur. Həndəsi modelləşdirmədə isə təpə vasitəsilə fiqurun hündürlüyü, bucaqları və ölçüləri hesablana bilər.
Hissələrə bölünmüş izah:
- Təpə və çoxbucaqlı fiqurlar:
Çoxbucaqlı fiqurun bütün küncləri təpə adlanır. Məsələn, kvadratın 4 təpəsi var. - Təpə və çoxüzlü fiqurlar:
Üçölçülü obyektlərin, məsələn, kubun və ya piramidanın bütün kəsişən nöqtələri təpədir. - Qraf nəzəriyyəsində təpə:
Burada təpələr əlaqələr şəbəkəsinin əsas düyünləri kimi çıxış edir və informasiyanın ötürülməsində, kompleks sistemlərin analizində əhəmiyyətlidir.
Riyaziyyatda üz, til, təpə anlayışlarının tətbiqi və tarixi inkişafı
Bu terminlərin hər biri qədim həndəsə məktəblərindən – qədim Misir, Babil, Yunan və Hindistan riyaziyyatından başlayaraq bu günə qədər öz aktuallığını qoruyub saxlayır. Müasir dövrdə isə bu anlayışlar topologiya, çoxölçülü həndəsə, arxitektura, qrafika, informatika və digər sahələrdə tətbiq olunur. Həndəsi obyektlərin modelləşdirilməsi, qraf strukturlarının qurulması, simmetriya və optimal yerləşdirmə problemləri, hətta müasir kriptoqrafiya və komputer elmlərində üz, til və təpə əsas qurucu elementlərdir.
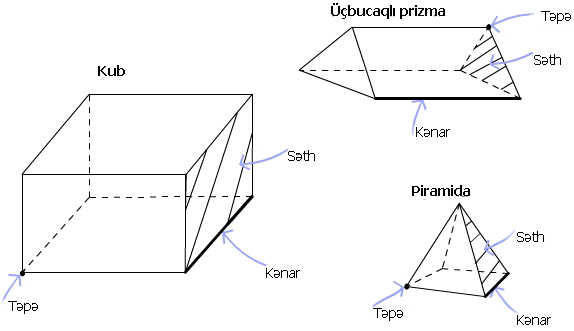
Üz, til və təpə anlayışlarının gündəlik həyatda rolu
Riyaziyyatın gündəlik həyatla birləşdiyi nöqtədə üz, til və təpə anlayışları konkret məkanları, binaları, alətləri, hətta təbiətdəki obyektləri (kristallar, poliedrlər, minerallar) təsvir etmək üçün istifadə olunur. Məsələn, bir evi təsvir edərkən pəncərənin və qapının üzləri, küncləri təpə, kənarları isə til adlandırılır. Konstruksiya və mühəndislik sahəsində bir obyektin dayanıqlılığı məhz bu elementlərin quruluşundan və əlaqəsindən asılıdır.
Üz, til və təpə ilə bağlı əsas riyazi düsturlar və əlaqələr
Ən məşhur və fundamental əlaqə Eyler düsturudur:
Təpə sayı – Til sayı + Üz sayı = 2
V – E + F = 2
Bu düstur bütün çoxüzlü fiqurlar üçün doğrudur və poliedrlərin əsas struktur əlaqəsini ifadə edir. Misal üçün, kub üçün:
V = 8, E = 12, F = 6
8 – 12 + 6 = 2
Qraf nəzəriyyəsində üz, til, təpə
Qraf nəzəriyyəsində üz, til və təpə anlayışları sistemlərin analizində, şəbəkələrin, nəqliyyat xəttlərinin, informasiya ötürülməsinin modelləşdirilməsində əsas vasitədir. Burada təpə məlumat nöqtəsini, til əlaqə xəttini, üz isə qapalı dövrəni və ya sistemin xarici sərhədini göstərir. Qraf nəzəriyyəsində düyün və kənarların sayı, üzlərlə olan əlaqəsi sistemin funksionallığını və optimallığını müəyyən edir.
Müasir texnologiyada üz, til, təpə modellərinin əhəmiyyəti
Kompyuter qrafikasında, 3D modelləşdirmədə hər bir fiqurun poliqonal təmsili üz, til və təpə massivlərinin toplusu ilə verilir. Hər bir obyektin səthi bir neçə üzdən ibarət olur, bu üzlərin kənarları til, onların kəsişdiyi nöqtələr isə təpədir. Bu modellər dizayndan tibbi avadanlıqlara, arxitektura layihələrindən kosmik tədqiqatlara qədər geniş tətbiq sahəsinə malikdir.
Üz, til, təpə anlayışlarının inkişafı və tədrisi
Azərbaycanda riyaziyyat tədrisinin bütün pillələrində – məktəb, kolleclər, universitetlər – bu terminlərin mənimsənilməsi xüsusi diqqət tələb edir. Riyaziyyatda məkan və forma hissinin inkişafı, həndəsi dünyagörüşün, analitik və məntiqi düşüncənin formalaşması məhz üz, til, təpə anlayışlarından başlayır. Hər bir şagird və tələbə üçün bu anlayışların praktik tətbiqi, riyazi modellərin qurulması, elmi və texniki inkişaf üçün bünövrədir.
Müasir riyaziyyatın daha dərin sahələrində, məsələn, topologiyada, çoxölçülü poliedrlərdə, dinamik sistemlərdə üz, til və təpənin analitik və abstrakt modelləri qurulur. Çoxölçülü obyektlərin, qrafik şəbəkələrin, informasiyanın optimal bölüşdürülməsinin riyazi əsası bu elementlərin qarşılıqlı əlaqəsində yatır.
Üz, til və təpə anlayışlarının gələcək texnoloji inkişafdakı rolu
Süni intellekt, 3D çap, avtomatlaşdırılmış layihələndirmə və materialşünaslıq kimi sahələrdə yeni obyektlərin modelləşdirilməsi, optimal konstruksiyaların hazırlanması, resursların düzgün bölüşdürülməsi üçün üz, til və təpə modelləri aktual və önəmli olaraq qalacaq. Gələcək riyazi innovasiyaların əsası məhz bu fundamental anlayışlar üzərində qurulacaq.
Riyaziyyatda üz, til və təpə anlayışları yalnız fiqurların təsviri üçün deyil, həm də müasir elmin, texnikanın, mühəndisliyin və gündəlik həyatın inkişafı üçün əsas rol oynayır. Məkanın, obyektlərin və proseslərin dəqiq və effektiv təsviri üçün bu anlayışların mənimsənilməsi, onların tətbiqi və tədrisi hər zaman mühüm vəzifədir. Riyazi bilik və yaradıcılıq üz, til, təpə kimi fundamental elementlərin təhlili və düzgün istifadəsi ilə zənginləşir.
Ən Çox Verilən Suallar
Riyaziyyatda üz çoxüzlü və ya çoxbucaqlı fiqurun iki ölçülü, düz, məhdud hissəsinə deyilir. Məsələn, kubun 6 üzü var və hər biri kvadrat formasındadır. Üzlər fiqurun səthini təşkil edir və həndəsi formanın görünüşünü müəyyənləşdirir.
Til çoxüzlü fiqurun iki üzünün kəsişdiyi xətt parçasıdır. Hər bir til iki təpəni birləşdirir və fiqurun konturunu müəyyən edir. Məsələn, kubda 12 til var və hər biri iki təpə arasında yerləşir.
Təpə çoxbucaqlı və ya çoxüzlü fiqurun bütün til və üzlərinin kəsişdiyi nöqtəyə deyilir. Təpələr fiqurun əsas dayaq nöqtələridir. Məsələn, kvadratın 4, kubun isə 8 təpəsi olur.
Eyler düsturu çoxüzlü fiqurlarda təpə (V), til (E) və üz (F) arasında əsas əlaqəni belə ifadə edir: V – E + F = 2. Bu düstur kub, piramida kimi fiqurlar üçün keçərlidir və onların əsas strukturunu riyazi şəkildə təsvir edir.
Düzgün çoxüzlü fiqurlar (kub, prizma, piramida, onikibucaqlı və s.), həndəsi bədənlər, poliedrlər və üçölçülü modellərdə üz, til, təpə anlayışları əsas elementlərdir. Kompüter qrafikasında, mühəndislikdə və memarlıqda da bu anlayışlar tez-tez rast gəlinir.
Qraf nəzəriyyəsində təpə ‘vertex’, til isə ‘edge’ adlanır. Təpələr qrafın əsas düyünləri, tillər isə onları birləşdirən əlaqələrdir. Hər bir qraf sistemin strukturunu təpə və tillər vasitəsilə təsvir edir.
Bu anlayışlar memarlıqda, konstruksiyada, mühəndislikdə, kompüter modelləşdirməsində, qrafika və dizaynda geniş tətbiq edilir. Evlərin, körpülərin, cihazların quruluşu, hətta təbiətdəki kristallar və mineralların təsviri üçün istifadə olunur.
Çoxüzlü fiqur (poliedr) səthi çoxsaylı üzlərdən ibarət olan üçölçülü fiqurdur. Hər üz iki və daha çox til ilə, hər til isə iki təpə ilə birləşir. Çoxüzlü fiqurun bütün səthi üzlərin məcmusu ilə yaranır.
Kompüter qrafikasında hər üçölçülü model üz, til və təpələrdən ibarət poliqonal şəbəkə şəklində qurulur. Hər səthi düz parça bir üz, kənarları til, onların kəsişmə nöqtələri isə təpə sayılır. Bu strukturlar obyektin real görüntüsünü yaratmaq üçün əsas rol oynayır.
Bu elementlərin sayı dəyişdikcə fiqurun forması, səth sahəsi, həcm və simmetriya xüsusiyyətləri də dəyişir. Üzlərin çoxluğu fiqurun daha mürəkkəb olmasına, təpə və tillərin artması isə onun strukturunun və sabitliyinin fərqlənməsinə səbəb olur.