Üçbucaqlı prizma riyaziyyatın və həndəsənin əsas fiqurlarından biri hesab olunur. Bu prizma həm təbiətdə, həm də texnologiyada, memarlıqda və istehsalatda müxtəlif sahələrdə geniş tətbiq olunur. Üçbucaqlı prizma, iki paralel və bir-birinə bərabər üçbucaq əsasdan və bu əsasları birləşdirən üç ədəd yan üzlərdən ibarət olan üçölçülü cisimdir. Onun hər bir üzü ya üçbucaq, ya da düzbucaqlı olur. Riyazi baxımdan belə prizma həm həndəsi təsvir baxımından, həm də məntiqi quruluş baxımından maraqlı hesab edilir. Üçbucaqlı prizmanın hər bir tərəfi, kənarları və bucaqları arasında sabit və dəqiq münasibətlər mövcuddur. Prizmanın formulu, həcmi, səthi və digər riyazi göstəriciləri ciddi qaydalara əsaslanır. Bu fiqur təhsil sisteminin müxtəlif pillələrində, xüsusilə də orta məktəbdən başlayaraq ali məktəblərə qədər riyaziyyat dərslərində dərindən öyrədilir.
Eyni zamanda, üçbucaqlı prizmalar təbiətdə, məsələn, kristalların formalaşmasında və ya bəzi memarlıq elementlərində rast gəlinir. Bütün bu sahələrdə üçbucaqlı prizmanın tətbiq imkanları onu riyazi və texniki baxımdan olduqca önəmli edir. Hazırda riyaziyyat elmi bu prizmanın xüsusiyyətlərini daha dərindən öyrənməyə və yeni tətbiq imkanlarını araşdırmağa davam edir. İctimai və elmi yanaşmada bu prizma həm klassik həndəsə, həm də müasir tətbiqi riyaziyyat üçün aktualdır.
Üçbucaqlı Prizmanın Riyazi Tərifi və Quruluşu
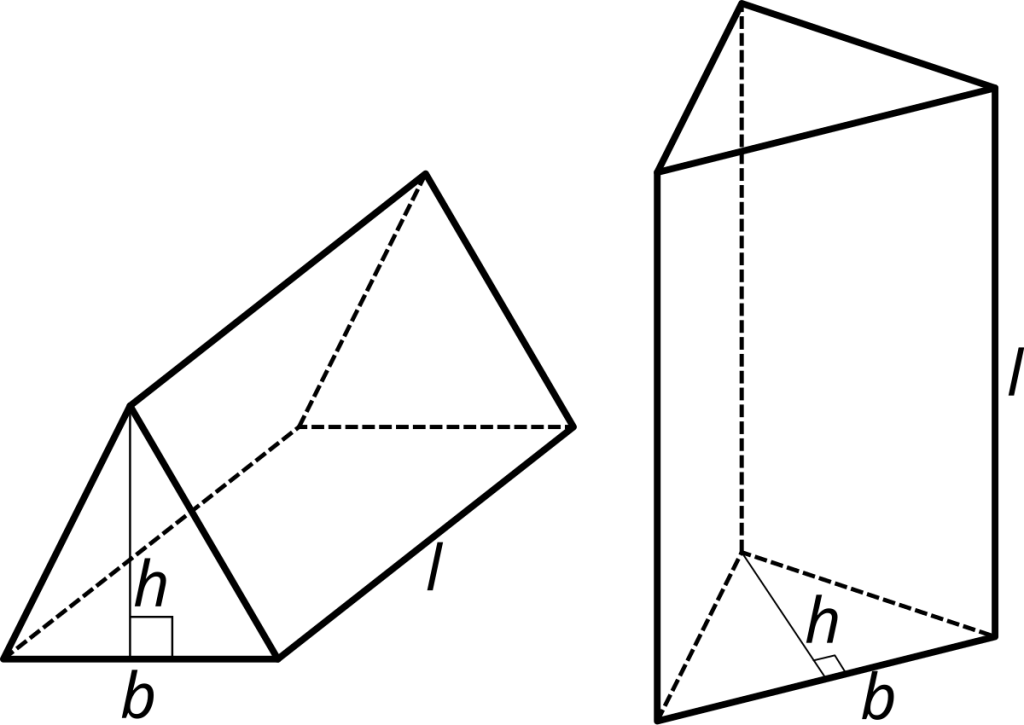
Üçbucaqlı prizma, əsasını təşkil edən iki bərabər və paralel üçbucağın və bu üçbucaqları birləşdirən üç paralel düzbucaqlı yan üzlərin birləşməsindən yaranan həndəsi cisimdir. Riyazi baxımdan bu prizma aşağıdakı şəkildə təsvir olunur: əsasları bərabər olan iki üçbucaq və yanları düzbucaqlı olan üç üz. Prizmanın bütün kənarları və zirvələri müəyyən riyazi əlaqəyə malikdir. Hər bir üçbucaqlı prizmanın ümumi səkkiz kənarı, altı üzü və altı zirvəsi olur. Prizmanın iki əsas üzü bərabər və paralel üçbucaqdan ibarətdir, digər üç üzü isə düzbucaqlıdır və bu üç düzbucaqlı üz əsasların müvafiq tərəflərini bir-birinə birləşdirir. Bu cür quruluş prizmanın sabitliyini və simmetriyasını təmin edir.
Üçbucaqlı prizmada istənilən kənarın uzunluqları əsas üçbucağın kənarlarının uzunluqlarına və prizmanın hündürlüyünə bağlıdır. Prizmanın hündürlüyü əsas üçbucaqlar arasındakı məsafədir və bu ölçü prizmada həcm və səth sahəsinin hesablanmasında əsas rol oynayır. Riyaziyyatda üçbucaqlı prizmalar istər elmi tədqiqatlarda, istərsə də məktəb dərsliklərində əsas həndəsi cisimlərdən sayılır. Onların xüsusiyyətləri, elementləri və formulaları müxtəlif riyazi məsələlərin həllində əsas rol oynayır. Üçbucaqlı prizmanın səthinin və həcminin tapılması, onun yan üzlərinin və əsaslarının sahəsinin hesablanması üçün xüsusi formullardan istifadə olunur. Həmçinin, üçbucaqlı prizmanın quruluşu həndəsi təsəvvürlərin inkişafında və riyazi düşüncənin formalaşmasında mühüm rol oynayır.
Üçbucaqlı Prizmanın Həcmi və Səthinin Hesablanması
Üçbucaqlı prizmanın əsas riyazi xüsusiyyətlərindən biri onun həcmi və səth sahəsinin hesablanmasıdır. Həcmin hesablanması üçün ilk növbədə prizmanın əsas üçbucağının sahəsi və prizmanın hündürlüyü müəyyən edilməlidir. Həcmin tapılması üçün aşağıdakı əsas formula tətbiq olunur:
Həcmin Formulu:
V = S × h
Burada V – prizmanın həcmi, S – əsas üçbucağın sahəsi, h – prizmanın hündürlüyüdür.
Əsas üçbucağın sahəsi isə riyaziyyatda tanınmış formullardan biri ilə hesablanır. Əgər əsas üçbucağın tərəfləri a, b, c-dirsə, Heron formulasından istifadə edilir:
S = √[p(p-a)(p-b)(p-c)]Burada p = (a+b+c)/2 üçbucağın yarıperimetri hesab olunur.
Prizmanın səth sahəsini hesablamaq üçün isə həm əsas üçbucaqların sahəsi, həm də yan düzbucaqlıların sahəsi nəzərə alınır. Ümumilikdə, səth sahəsi aşağıdakı kimi hesablanır:
Səth Sahəsinin Formulu:
A = 2 × S + P × h
Burada A – səth sahəsi, S – əsas üçbucağın sahəsi, P – əsas üçbucağın perimetri, h – prizmanın hündürlüyüdür.
Prizmanın bütün səthi yan və əsas səthlərin cəmi kimi qəbul edilir. Səth sahəsinin hesablanması həm praktik, həm də nəzəri riyaziyyatda əhəmiyyətli yer tutur. Həcmin və səthin düzgün hesablanması, riyazi cisimlərin konstruksiyası və onlardan istifadə üçün vacibdir.
Üçbucaqlı Prizmanın Tarixi və Təbii Nümunələri
Üçbucaqlı prizma antik dövrlərdən bəri həndəsə elminin diqqət mərkəzində olub. Yunan riyaziyyatçılarından tutmuş, orta əsr islam alimlərinə qədər bir çox məşhur şəxsiyyət üçbucaqlı və digər həndəsi cisimlərin təhlilinə böyük önəm veriblər. Üçbucaqlı prizmanın təbiətdə də bir sıra nümunələri mövcuddur. Məsələn, bəzi minerallar və kristallar üçbucaqlı prizma formasında olur. Bu, onların molekulyar strukturlarında xüsusi nizamın mövcudluğunu göstərir.
Arxeoloji qazıntılar zamanı qədim dövrlərə aid bəzək əşyaları, silah ucluqları və digər əşyaların da bəzən üçbucaqlı prizma formasında olduğu aşkarlanıb. Orta əsrlərdə, xüsusilə də Şərq alimləri bu cisimləri optik linzaların və işıq prizmasının əsas quruluşu kimi istifadə ediblər. Memarlıqda isə üçbucaqlı prizmanın forması həm antik, həm də müasir tikililərdə dekorativ və daşıyıcı element kimi tətbiq edilib. Riyaziyyatın inkişafı ilə üçbucaqlı prizmanın quruluşu və riyazi xüsusiyyətləri daha ətraflı şəkildə araşdırılmış və yeni elmi nəticələr əldə edilmişdir.
Üçbucaqlı Prizmanın Təhsil Sistemi və Tətbiqi
Üçbucaqlı prizmanın öyrədilməsi Azərbaycanda riyaziyyat təhsilinin müxtəlif pillələrində mühüm yer tutur. Orta məktəb proqramlarında həndəsi fiqurların, xüsusilə də prizmaların əsas anlayışları dərindən izah edilir. Riyaziyyat dərslərində, üçbucaqlı prizmanın əsas xüsusiyyətləri, onun həcmi, səth sahəsi və digər parametrləri praktiki misallar üzərində öyrədilir. Prizmanın qrafik təsviri, maketinin hazırlanması və ölçülərinin hesablanması şagirdlərin məntiqi düşüncə bacarıqlarını inkişaf etdirir.
Ali təhsil səviyyəsində isə prizmanın tədqiqi daha dərin və elmi səviyyədə aparılır. Riyaziyyat və mühəndislik fakültələrində üçbucaqlı prizmanın kompleks formaları, onların məkan və tətbiqi həndəsədə rolu, simmetriya və analitik həndəsə ilə əlaqəsi dərindən öyrədilir. Riyaziyyat ixtisası üzrə təhsil alan tələbələr prizmanın alqoritmlərini, onun riyazi modellərini və praktiki tətbiq sahələrini tədqiq edirlər. Müəllim hazırlığı fakültələrində isə üçbucaqlı prizmanın tədris metodikası, təlim vəsaitlərinin hazırlanması və interaktiv dərs modellərinin qurulması əsas mövzulardan biridir.
Aşağıdakı cədvəldə Azərbaycanda müxtəlif təhsil pillələri üzrə üçbucaqlı prizma mövzusunun tədrisi ilə bağlı məlumat verilmişdir:
| Təhsil Pilləsi | Dərs Mövzusu | Əsas Məqamlar | Qəbul Qaydası |
|---|---|---|---|
| Orta məktəb | Həndəsi fiqurlar | Prizmanın quruluşu, əsas və yan səthləri, həcmin hesablanması | Müəyyən siniflər üçün məcburi mövzu |
| Ali məktəb (bakalavr) | Tətbiqi həndəsə | Prizmanın analitik təsviri, modelləşdirilməsi | Riyaziyyat, mühəndislik fakültələri |
| Magistratura/doktorantura | Riyazi tədqiqatlar | Üçbucaqlı prizmanın xüsusi modelləri və proqramlaşdırma | Elmi-tədqiqat mərkəzləri |
Üçbucaqlı Prizmanın Tətbiq Sahələri və Praktik Əhəmiyyəti
Üçbucaqlı prizmanın tətbiq sahələri olduqca genişdir. İlk növbədə, memarlıq və inşaatda üçbucaqlı prizma forması dayanıqlı və estetik konstruksiyalar üçün istifadə olunur. Bu cisimlər müxtəlif binaların dam örtüklərində, körpülərin dayaq hissələrində, müasir memarlıqda isə dekorativ element kimi seçilir. Aviasiyada və avtomobil sənayesində aerodinamik modellərdə üçbucaqlı prizma forması hava müqavimətini azaltmaq üçün tətbiq edilir.
Optikada işıq şüalarının sınması və dispersiyası üçün prizma formalarından, xüsusilə də üçbucaqlı prizmalardan istifadə edilir. Hər bir prizmanın optik xüsusiyyətləri onun içindən keçən işıq şüasının istiqamətini dəyişdirmək və spektral analiz aparmaq üçün olduqca əlverişlidir. Təbiətdə isə bəzi kristal və minerallar üçbucaqlı prizma şəklində böyüyür ki, bu da onların fiziki və kimyəvi xüsusiyyətlərini müəyyənləşdirir.
Sənaye istehsalatında, xüsusilə də materialların kəsilməsi, montajı və texniki dizaynda üçbucaqlı prizmalar geniş istifadə olunur. Onlar həmçinin mühəndislik layihələrində, texnoloji qurğularda və mexaniki alətlərdə əsas komponent kimi nəzərdə tutulur. Təhsil prosesində isə bu prizma şagird və tələbələrin məkan təsəvvürünü və analitik bacarıqlarını inkişaf etdirmək üçün əvəzsiz vasitədir.
Üçbucaqlı Prizmanın İxtisaslar və Fakültələr üzrə Əhəmiyyəti
Azərbaycanda və dünyada riyaziyyat, mühəndislik, memarlıq, fizika, optika və dizayn ixtisaslarında üçbucaqlı prizmanın nəzəri və praktik əhəmiyyəti böyükdür. Riyaziyyat fakültələrində prizmanın riyazi xüsusiyyətləri, onun həndəsi və analitik təsviri xüsusi dərsliklər və kurslar vasitəsilə öyrədilir. Mühəndislik və memarlıq fakültələrində üçbucaqlı prizmaların modelləri, layihələndirilməsi və tətbiq sahələri praktiki məşğələlərlə müşayiət olunur.
Fizika və optika ixtisaslarında prizmanın işıq və dalğa optikasında rolu, dispersiya və işıq sınması hadisələrinin öyrənilməsi üçün istifadə edilir. Texnologiya və sənaye dizaynı üzrə təhsil alan tələbələr isə üçbucaqlı prizma formalı qurğuların hazırlanmasını, onların funksionallığını və estetik cəhətlərini öyrənirlər.
Aşağıdakı cədvəldə üçbucaqlı prizmanın öyrədildiyi əsas fakültələr və ixtisaslar göstərilib:
| Fakültə / İxtisas | Prizmanın Öyrədildiyi Mövzu | Praktik Tətbiq |
|---|---|---|
| Riyaziyyat | Həndəsi fiqurlar, analitik həndəsə | Riyazi modelləşdirmə |
| Mühəndislik | Konstruksiya, dizayn | Layihələndirmə və quruculuq |
| Memarlıq | Tikinti, struktur modellər | Binaların və körpülərin layihələndirilməsi |
| Fizika / Optika | İşıq sınması və dispersiya | Optik cihazların hazırlanması |
| Dizayn və texnologiya | Estetik və funksional modellər | Texniki dizayn və montaj |
Üçbucaqlı Prizmanın Əhəmiyyəti və Gələcək Tədqiqat İstiqamətləri
Üçbucaqlı prizmanın riyazi, texnoloji və tətbiqi əhəmiyyəti illər keçdikcə daha da artır. Bu prizmanın öyrənilməsi və tətbiqi yalnız nəzəri riyaziyyatla məhdudlaşmır, eyni zamanda yeni texnoloji sahələrdə və sənaye dizaynında da öz əksini tapır. İndiki dövrdə üçbucaqlı prizmanın müxtəlif variasiyalarının elmi araşdırılması davam edir. Kompüter qrafikası, virtual reallıq və 3D modelləşdirmədə bu prizmanın yeni formaları işlənib hazırlanır.
Azərbaycanın elmi mühiti və təhsil sistemi bu sahədə müasir tələblərə cavab verən proqramlar hazırlayır. Riyaziyyat və texnika ixtisasları üzrə elmi-tədqiqat işləri üçbucaqlı prizmaların yeni növlərinin və onların müxtəlif sahələrdə tətbiq imkanlarının araşdırılmasına yönəlib. Gələcəkdə bu sahədə innovativ layihələrin və yeni tədris metodlarının inkişafı gözlənilir.
Üçbucaqlı prizma həm klassik riyaziyyatın, həm də müasir texnologiyanın ən maraqlı və aktual həndəsi cisimlərindən biri olaraq qalır. Onun strukturu, hesablama qaydaları və müxtəlif sahələrdəki tətbiq imkanları riyaziyyat elmi və təhsil sistemi üçün əvəzsiz əhəmiyyət daşıyır. Üçbucaqlı prizmanın riyazi modelləşdirilməsi, səth və həcminin hesablanması, eləcə də real həyatda memarlıqdan tutmuş, optikaya, sənaye dizaynına qədər müxtəlif istiqamətlərdə istifadə olunması onu praktik və nəzəri baxımdan vacib cisimlərdən birinə çevirir. Azərbaycanda və dünyada bu prizmanın tədrisi və öyrənilməsi davam edir, yeni elmi və texnoloji nəticələr əldə edilir. Həm şagirdlər, həm də mütəxəssislər üçün üçbucaqlı prizma riyazi və məntiqi düşüncənin inkişafı baxımından vacib fiqur hesab olunur
Ən Çox Verilən Suallar
Üçbucaqlı prizma iki paralel və bərabər üçbucaqlı əsasdan və bu əsasları birləşdirən üç düzbucaqlı yan üzdən ibarət üçölçülü həndəsi fiqurdur. Onun ümumilikdə altı üzü (iki əsas, üç yan), doqquz kənarı və altı zirvəsi olur. Prizmanın bütün yan və əsas səthləri bir-birinə perpendikulyar və paralel yerləşir.
Üçbucaqlı prizmanın həcmi üçün əsas üçbucağın sahəsi ilə prizmanın hündürlüyü vurulur. Yəni V = S × h, burada S əsas üçbucağın sahəsi, h isə əsaslar arasındakı məsafədir. Əsas üçbucağın sahəsi Heron düsturu və ya adi sahə düsturu ilə tapılır.
Səth sahəsini hesablamaq üçün iki əsas üçbucağın sahəsi və üç yan düzbucaqlının sahələri toplanır. Ümumi düstur belədir: A = 2 × S + P × h, burada S əsas üçbucağın sahəsi, P isə əsas üçbucağın perimetri, h isə prizmanın hündürlüyüdür.
Üçbucaqlı prizmalar memarlıqda, mühəndislikdə, optikada, aviasiyada, sənaye dizaynında, təbiətdə kristal formalarında və hətta tədris vasitələrində istifadə olunur. Bu cisimlər, dayanıqlı konstruksiyaların və müxtəlif texniki qurğuların hazırlanmasında xüsusi rol oynayır.
Orta məktəblərdə həndəsi fiqurlar mövzusunda, ali məktəblərdə isə riyaziyyat, mühəndislik, memarlıq, fizika və texnologiya ixtisaslarında üçbucaqlı prizma dərindən öyrədilir. Eyni zamanda, bu mövzuya metodik və tətbiqi səviyyədə yanaşılır.
Sadə didaktik maketlər məktəb üçün 5-30 manat arası, peşəkar laboratoriya modelləri isə 100-500 manat və daha yüksək qiymətə satılır. Rəqəmsal proqram təminatı və 3D modellər üçün isə qiymətlər 20-300 manat arasında dəyişir.
Riyaziyyat, mühəndislik, memarlıq, fizika, optika və sənaye dizaynı ixtisaslarında üçbucaqlı prizma xüsusi dərs mövzusu kimi tədris olunur. Hər bir ixtisasda bu prizmanın praktik və nəzəri aspektləri ayrıca öyrədilir.
Ən çox rast gəlinən səhv yan üzlərin sahəsini və əsasların perimetrini səhv hesablamaqdır. Eyni zamanda, əsasların və yanların düzgün ölçülməməsi, düsturların yanlış tətbiqi də nəticənin səhv çıxmasına səbəb ola bilər.
Əgər üçbucağın bütün tərəfləri məlumdursa, Heron düsturu (S = √[p(p-a)(p-b)(p-c)], p=(a+b+c)/2) istifadə edilir. Hündürlüyü və əsas tərəfi məlumdursa, S = (a×h)/2 düsturu tətbiq olunur.
Gələcəkdə üçbucaqlı prizmaların kompüter qrafikası, 3D modelləşdirmə, virtual reallıq texnologiyaları və yüksək texnologiyalı sənaye sahələrində daha geniş tətbiqi gözlənilir. Elmi-tədqiqat işlərində və innovativ dizayn layihələrində prizma modelləri xüsusi yer tuta bilər.