Xətti Tənliklər Sisteminin Həll Üsulları :

Xətti tənliklər sistemi riyaziyyatın əsas anlayışlarından biridir və gündəlik həyat, iqtisadiyyat, mühəndislik və fizika sahələrində geniş tətbiq olunur. Xətti tənliklər sistemi bir və ya bir neçə dəyişəni olan xətti tənliklərin birlikdə araşdırılması və həllinə əsaslanır. Bu məqalədə xətti tənliklər sistemlərinin həlli üsulları, metodları, nəzəri əsasları və praktik tətbiqləri geniş şəkildə izah olunacaq.

Xətti Tənlik və Sistem Nədir?

Xətti tənlik – dəyişənlərdən yalnız birinci dərəcəli ifadələr olan tənlikdir. Məsələn, ax+by=cax + by = cax+by=c tənliyi xətti tənlikdir. Xətti tənliklər sistemi isə bir neçə xətti tənliyin birlikdə verildiyi struktur olaraq aşağıdakı kimi ifadə olunur: {a1x+b1y=c1a2x+b2y=c2\begin{cases} a_1x + b_1y = c_1\\ a_2x + b_2y = c_2 \end{cases}{a1​x+b1​y=c1​a2​x+b2​y=c2​​

Burada xxx və yyy dəyişənlərdir və məqsəd onların uyğun dəyərlərini tapmaqdır. Sistem bir, iki və ya daha çox dəyişəni əhatə edə bilər. Xətti tənliklər sisteminin həlli metodları əsasən tənliklərin sayı və dəyişənlərin sayına görə seçilir.

Xətti Tənliklər Sisteminin Həllinin Əsas Prinsipləri

Xətti tənliklər sisteminin həllində bir neçə əsas prinsip var:

• Uyğunluq – tənliklərin həll olunması üçün dəyişənlərin uyğun qiymətləri olmalıdır.
• Müstəqillik – tənliklər bir-birindən asılı olmamalıdır, yəni hər biri sistemə özəl məlumat əlavə etməlidir.
• Dəqiqlik – həll prosesi riyazi dəqiqliklə aparılmalıdır, tərtib olunan nəticələr doğru və yoxlanılabilir olmalıdır.
• Qrafik yanaşma – tənliklər qrafik vasitəsilə təmsil edilə bilər və həll nöqtəsi qrafikdə kəsişmə nöqtəsi kimi göstərilir.

Bu prinsiplər sistemin həllində nəzərə alınmalıdır ki, nəticələr riyazi baxımdan düzgün olsun.

Həll Üsulları

Xətti tənliklər sisteminin həlli üçün müxtəlif üsullar mövcuddur. Ən çox istifadə olunan üsullar aşağıdakılardır:

1. Əvəz etmə Metodu

Əvəz etmə metodu iki tənlikli sistemlərdə geniş istifadə olunur. Metodun mərhələləri:

1. Bir tənlikdən bir dəyişəni ifadə etmək.
2. Bu ifadəni digər tənlikdə əvəz etmək.
3. Sadələşdirilmiş tənlikdən dəyişənin qiymətini tapmaq.
4. Tapılmış dəyişəni ilkin tənlikdə əvəz edərək digər dəyişəni tapmaq.

Məsələn: {x+y=52x−y=1\begin{cases} x + y = 5\\ 2x – y = 1 \end{cases}{x+y=52x−y=1​

Birinci tənlikdən y=5−xy = 5 – xy=5−x əldə edilir. Sonra 2x−(5−x)=12x – (5 – x) = 12x−(5−x)=1 həlli ilə x=2x = 2x=2 tapılır. Sonra y=3y = 3y=3.

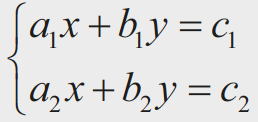
2. Qaydaya görə Toplama Metodu

Toplama və çıxarma üsulu tənlikləri bir-birinə əlavə və ya çıxmaq yolu ilə bir dəyişəni ləğv etməyə əsaslanır. Məsələn: {2x+3y=8x−3y=4\begin{cases} 2x + 3y = 8\\ x – 3y = 4 \end{cases}{2x+3y=8x−3y=4​

Tənlikləri topladıqda: 3x=123x = 123x=12, x=4x = 4x=4. Daha sonra y=−43y = -\frac{4}{3}y=−34​.

3. Matriks və Determinantlar Metodu (Cramer Qaydası)

Cramer Qaydası lineyar tənliklər sistemini determinantlar vasitəsilə həll etməyə imkan verir. Əsas prinsiplər:

• Sistem nnn dəyişən və nnn tənlikdən ibarət olmalıdır.
• Matriks deteminantı sıfır olmamalıdır.

Əgər sistem: a1x+b1y=c1,a2x+b2y=c2a_1x + b_1y = c_1, \quad a_2x + b_2y = c_2a1​x+b1​y=c1​,a2​x+b2​y=c2​

Δ=∣a1b1a2b2∣\Delta = \begin{vmatrix} a_1 & b_1 \\ a_2 & b_2 \end{vmatrix}Δ=​a1​a2​​b1​b2​​​
Δx=∣c1b1c2b2∣\Delta_x = \begin{vmatrix} c_1 & b_1 \\ c_2 & b_2 \end{vmatrix}Δx​=​c1​c2​​b1​b2​​​, x=Δx/Δx = \Delta_x / \Deltax=Δx​/Δ və Δy=∣a1c1a2c2∣\Delta_y = \begin{vmatrix} a_1 & c_1 \\ a_2 & c_2 \end{vmatrix}Δy​=​a1​a2​​c1​c2​​​, y=Δy/Δy = \Delta_y / \Deltay=Δy​/Δ.

4. Qrafik Metodu

Qrafik metodu tənlikləri koordinat müstəvisində əks etdirməyə əsaslanır. Hər tənlik xətt kimi çəkilir və sistemin həlli xəttlərin kəsişmə nöqtəsində olur. Bu üsul vizual anlamağa kömək edir və xüsusilə tələbələr üçün effektivdir.

5. İnvers Matriks Metodu

Bu üsul yalnız kvadrat sistemlər üçün uyğundur. Sistem AX=BAX = BAX=B formasında yazılır. Əgər A−1A^{-1}A−1 mövcuddursa, X=A−1BX = A^{-1}BX=A−1B hesablanır. Bu metod kompüter proqramları və mürəkkəb sistemlər üçün əlverişlidir.

6. Gauss Eliminasiya Metodu

Gauss eliminasiya üsulu çox dəyişənli sistemlər üçün effektivdir. Metod aşağıdakı mərhələləri əhatə edir:

• Əsas dəyişən seçilir.
• Tənliklər sadələşdirilir.
• Triangular forma yaradılır.
• Sonra geri əvəz etmə yolu ilə həll tapılır.

Bu üsul mürəkkəb və böyük sistemlərdə çox faydalıdır.

Sistem Nəticələrinin Tipi

Xətti tənliklər sisteminin həlli nəticəsində aşağıdakı hallar mümkündür:

• Bir unikal həll – tənliklər bir-birini tamamlayır və dəyişənlər üçün konkret qiymətlər mövcuddur.
• Həllsiz sistem – tənliklər bir-birinə uyğun deyil, heç bir həll yoxdur.
• Sonsuz həll – tənliklər asılıdır və dəyişənlər üçün sonsuz həll dəsti mövcuddur.

Bu nəticələr sistemin determinanta və xəttlərin yerləşməsinə görə müəyyən edilir.

Xətti Tənliklərin Praktik Tətbiqi

Xətti tənliklər sistemləri müxtəlif sahələrdə istifadə olunur:

• Mühəndislik və fizika – gərginlik, axım, temperatur və digər parametrlərin hesablanması
• İqtisadiyyat və maliyyə – büdcə və resursların bölüşdürülməsi, balans analizi
• Kompüter elmləri – qrafik təsvirlər və proqramlaşdırma problemləri
• Statistika və optimallaşdırma – ən kiçik kvadratlar metodu və tədqiqat problemləri

Bu sahələrdə xətti tənliklərin həlli real həyatda mühüm əhəmiyyət kəsb edir.

Təhsil və Öyrənmə

Xətti tənliklər sistemlərinin öyrənilməsi riyaziyyat təhsilinin vacib hissəsidir. Tələbələr üçün bu, analitik düşünmə bacarıqlarının inkişafını təmin edir və gələcək elmi və peşəkar fəaliyyət üçün zəmin yaradır. Əsas anlayışların mənimsənilməsi, müxtəlif həll üsullarının tətbiqi tələbələrin analitik və kritik düşüncə qabiliyyətini artırır.

Xətti tənliklər sistemlərinin həlli riyaziyyat və tətbiqi sahələrdə fundamental rol oynayır. Əvəz etmə, toplama, Cramer Qaydası, qrafik, invers matriks və Gauss eliminasiya metodları müxtəlif mürəkkəblikdəki sistemlər üçün geniş istifadə olunur. 2025-ci ildə bu üsullar həm təhsil, həm də texniki sahələrdə daha da effektiv və rəqəmsal proqramlarla birlikdə tətbiq ediləcək. Xətti tənliklərin öyrənilməsi və həlli analitik düşüncə, problem həll etmə bacarıqları və praktiki tətbiqlər üçün əvəzsizdir.

Ən Çox Verilən Suallar