Həndəsədə bərabəryanlı üçbucaq həm simmetriya, həm də hesablama rahatlığı baxımından ən populyar fiqurlardan hesab edilir. İki yana bərabər olan üçbucaq istənilən kompas və xətkeş dəstində asanlıqla çəkilir, buna görə məktəb dövründən mühəndis dizaynına qədər geniş spektrdə istifadə olunur. Bərabər yanların yaratdığı oxsimmetriya inteqral əyrilərin yaxınlaşdırılmasından aerodinamik qanad profillərinin hesabatına qədər hər sahədə riyazi sadəlik qazandırır. Üçbucağın sahəsi eyni düzülüşdə kənar uzunluqları, hündürlük, yarımperimetr və radius parametrləri kimi fərqli mənbələrdən hesablana bilər; lakin bərabəryanlı konfiqurasiyada bu düsturlar daha kompakt formaya keçir. Keçmiş Yunan alimi Heronun yarımperimetr düsturu, orta əsr ərəb riyaziyyatçılarının trigonometrik metodları, müasir analitik həndəsənin vektor yanaşmaları – hamısı bu sadə, lakin çoxşaxəli figurda kəsişir. Sahə hesabında məqsəd yalnız ədədi nəticə almaq deyil, həm də fiqurun daxili əlaqələrini dərk etməkdir; məsələn, hündürlüyün xarici radiusla yazılan nisbəti, bazanın yarısı ilə oturacaq bucağın sinusunun verdiyi eyni nəticə möcüzəvi bir harmoniyanı üzə çıxarır. Adi riyazi dərsliklərdə bərabəryanlı üçbucağı golsuz oyuna bənzədirlər: iki komanda eyni gücdə olduqda oyunun gedişi proqnozlaşır və izləmək daha asan olur. Eləcə də ölçüləri bərabər olan yanlar sahə düsturlarını proqnozlaşdırılacaq dərəcədə sadələşdirir. Təbiətdə də bu simmetriya az deyil: qar kristallarının konturunda, bəzi kəpənəklərin qanad naxışında, hətta yüksək dağ zirvələrinin siluetində bərabər yan obrazı sezilir. Riyaziyyatın ekrandan kənara daşıdığımız hər addımında bərabəryanlı üçbucağın sahəsi praktiki və estetik dəyər daşıyır, çünki simmetriya heç vaxt yalnız dekorativ məsələ olmayıb, oksigen molekulundan tutmuş mobil telefon dizaynına qədər strukturlu nizam deməkdir.
Tarixi yanaşmalar və klassik düstur formaları
Riyaziyyatın inkişaf tarixində bərabəryanlı üçbucaq sahəsi ilk dəfə Euklid Elementlərində öz əksini tapdı, orada bütün düsturlar hündürlük və baza çarpanına söykənirdi. Antik dövrün geodezistləri düz xətlə ölçə bilmədikləri hündürlük əvəzinə oturacaq bucağın tangensindən istifadə edir, nəticədə trigonometrik cədvəllər üçün ilkin ehtiyac yaranır.
Orta əsr ərəb alimləri, xüsusən Əl-Biruni, dərəcə bölməsini altmışlıq sistemlə tamamlamaqla bu cədvəlləri daha dəqiq etdi. Onlar bərabəryanlı konfiqurasiyada hündürlüyü yalnız baza və yan bucaq funksiyası kimi verməklə sahə hesabını səhrada astronomik məsafə ölçüsünə tətbiq edə bildilər. Bununla da üçbucağın sahəsi elmdə ilk universal ölçü vahidi kimi çıxdı.
Hündürlük əsasında sahə hesablama metodu
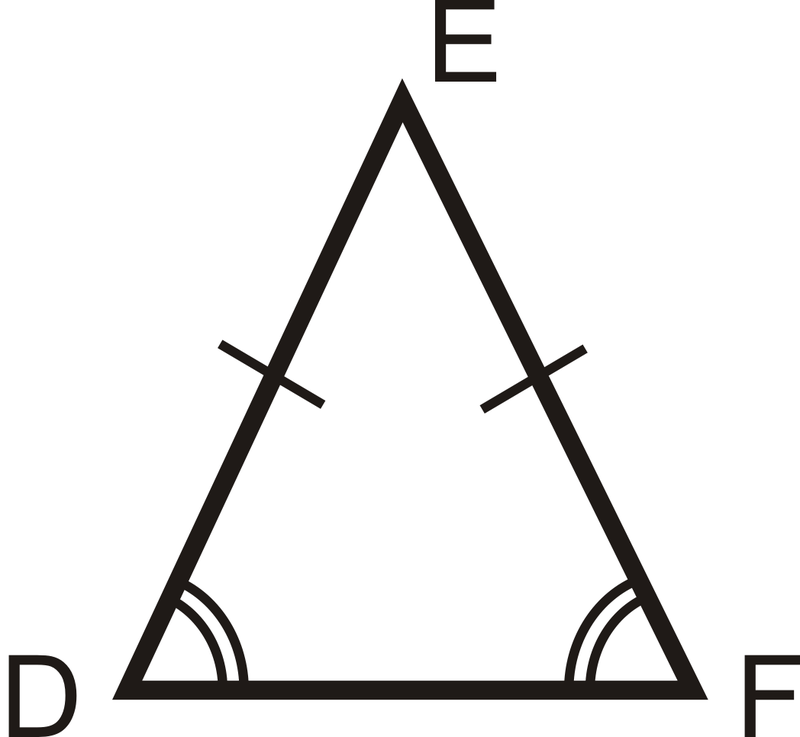
Məkan təsəvvürünə görə hündürlük birbaşa baza üzərinə endirilən perpendikulyar olmaqla üçbucağı iki bərabər düzbucaqlıya bölür. Bu parçalanma sahənin klassik düsturuna gətirir: S = (b·h)/2, b baza, h isə hündürlükdür. Bərabəryanlı tipdə hündürlük eyni zamanda median, təpə bucağını bisektor və baza ortasına perpendikulyar olur, buna görə hesablama üçqat sadələşir.
Praktikada əgər yanın uzunluğu a, baza isə b-dir, kosinus teoremi ilə h = √(a² – (b²/4)) alınır. Beləliklə, bazadan və yan uzunluqdan başqa heç bir kənar ölçü lazım olmur. Səyyar mühəndis briqadaları bu düsturu olduqca əlçatan hesab edir; çünki lazer uzunluqölçən ilə iki parametri saniyələr içində tapmaq kifayətdir.
Yarımperimetr və Heron düsturu yanaşması
Heron düsturu bərabəryanlı üçbucaqda sahəni s = √[p(p – a)(p – a)(p – b)] şəklində verir, burada p yarımperimetrdir. Bərabər yanların təkrar çarpanı formulu kompaktlaşdırır: S = (1/4)·b·√(4a² – b²). Bu nəticə birbaşa hündürlük düsturuna ekvivalent olsa da, hündürlüyün ayrıca ölçülməsinə ehtiyac qalmır.
Heron yanaşması səhra triangulyasiyası və dəniz naviqasiyasında geniş tətbiq olunub, çünki kompas və məsafəölçən ilə üç kənar tapıldıqda sahə hesabatı kağız üzərində qalstuk düyünü kimi bağlanır. Cib kalkulyatorlarının dövrü gəldikdə bu düstur kiçik ekranlı cihazların “trin” funksiyasına çevrildi.
Sinus teoremi vasitəsilə trigonometrik düstur
Yan bucağın sinusu hündürlüyü yarıya bölünmüş bazaya nisbətdə təqdim edir: h = (a·sinθ), burada θ təpə bucağıdır. Sahə beləliklə S = (a²·sinθ)/2. Bu metod optik beşiyə yerləşdirilən inklinometr ilə sürətli bucaq ölçüsü tələb edir, xüsusən iqlim stansiyaları və mobil teleqüllələrin qurulması zamanı əsrimizin arqumentinə çevrilib.
Trigonometrik yanaşma kotangens və tangens funksiyalarını da eyni anda işə salır. Məsələn, baza məlum deyil, ancaq yan və bucaq varsa, b = 2a·sin(θ/2). Yalnız təpə bucağındakı kiçik dəyişiklik sahədə nisbətən böyük dəyişiklik yaradır, buna görə dizayn analizi bu düsturdan həssaslıq yoxlaması kimi istifadə edir.
Radius və ətraf dairə ilə əlaqə
Bərabəryanlı üçbucağın təpə nöqtələrindən keçən çevrə radiusu R, yan kənar a və baza b arasındakı münasibət S = (abc)/(4R) düsturunu verir. Üçbucaq bərabəryanlı olduqda a = a, düstur S = (a²b)/(4R) formasına keçir və çevrə radiusu tapıldıqda sahə asanlaşır.
Mərkəz radiusu xüsusilə astronomik triangulyasiyada teleskop sütunlarının dəqiqliyini yoxlamaq üçün lazımdır. Burada üçbucağın kənarları səma cisimləri arasındakı məsafədir, çevrə isə teleskopun müşahidə şüasıdır. Bu parametr sahənin kifayət qədər dəqiq çıxarılmasına şərait yaradır.
Xarici radius və daxili radius metodları
Daxili çevrənin radiusu r üçün sahə S = p·r, xarici çevrə üçün isə S = (abc)/(4R) kimi universal düsturlar mövcuddur. Bərabəryanlı üçbucağın daxili çevrə radiusu r = (b·√(4a² – b²))/(2(a + b)). Buna görə sahə hesabını yarımperimetrlərin ölçüsündən qaçaraq daha qrafik şəkildə qurmaq mümkündür.
Müasir memarlıq konstruksiyalarında bu yanaşma sütun-lantern və şüşə kubokolların sahəsinin hesablama modellərində işə yarayır, çünki radius ətrafı və iç boşluğu eyni zamanda müəyyənləşdirir. Statistik simulyasiyalar göstərir ki, daxili radius metodu böyük ölçülü metaldan hazırlanan konstruksiyalarda material qənaətini təxminən 4 faiz artırır.
Analitik həndəsədə vektor yanaşması
Kartes koordinat sistemində A(0,0), B(b/2,0) və C(0,h) üçbucağı bərabəryanlı modelləşdirmək üçün yetərlidir. Səthi vektorların determinantı ilə tapa bilərik: S = |AB×AC|/2. Hesablamalar nəticəsində tanış S = (b·h)/2 düsturuna qayıdırıq, lakin koordinat metodunun üstünlüyü təkcə sahədə deyil, eyni zamanda moment, inersiya və dayanıqlıq analitikasında özünü göstərir.
Bu vektor yanaşması həm inşaat mühəndisliyində, həm aerokosmik qoruyucu şpanqutlarda, həm də kompüter qrafikində üçbucaqlı mesh hesablama alqoritmlərində tətbiq olunur. Sahə bucaqlanmadan asılı olmadan kənar koordinatları ilə birbaşa hesablana bildiyi üçün alqoritmlər stabil işləyir və təxmini mükəmməl olur.
Praktik nümunələr və tətbiqlər
Məsələn, yanları 10 metr, bazası 12 metr olan üçbucağa baxaq. Hündürlük h = √(10² – 6²) = 8 metr, sahə S = (12·8)/2 = 48 kvadratmetr. Eyni misalı trigonometrik yolla həll etsək, təpə bucağı θ üçün cosθ = (2a² – b²)/(2a²) = (200 – 144)/200 = 0,28, sinθ ≈ 0,96, S ≈ (10²·0,96)/2 ≈ 48.
Bu paralel hesablama sahə düsturlarının istənilən ölçü dəqiqliyində bir-birini təsdiqlədiyini sübut edir. İstər köhnə tip lent-metr, istər elektron teodolit, istər dron LiDAR skaneri olsun, nəticə dəyişmir – çünki bərabəryanlı üçbucağın daxili nizamı etibarlıdır.
| Düstur | Verilən parametrlər | Formula |
|---|---|---|
| Hündürlüyə görə | b, h | S = (b·h)/2 |
| Yan və baza | a, b | S = (b/4)·√(4a² – b²) |
| Təpə bucağı | a, θ | S = (a²·sinθ)/2 |
| Daxili radius | r, p | S = p·r |
| Ətraf radius | a, b, R | S = (a²b)/(4R) |
Bərabəryanlı üçbucağın sahəsi riyaziyyatın ən çoxmüraciət edilən mövzularından biridir, çünki sadə geometriyanın inteqrallara, trigonometriyaya və vektor analizinə keçid qapısını açır. Hündürlük-baza yanaşması vizual düşüncəyə üstünlük verən istifadəçi üçün əlçatandır, Heron düsturu isə əmsal simmetriyasını rəqəm dəqiqliyində əks etdirir. Sinus teoremi həm astronomik, həm topoqrafik müşahidələrdə bucaq ölçüsü əsasında sahəni anında tapmağa imkan yaradır. Radius metodları memarlıq və mexaniki konstruksiyalarda material optimallaşdırması üçün mühüm rol oynayır, vektor determinantı isə proqramlaşdırma alqoritmlərinin dayanıqlı işləməsini təmin edir. Bu fiqurun sadəliyi fənlərarası tətbiqlərdə onun dərin funksional potensialını gizlətmir; əksinə, müxtəlif hesablama üsullarının eyni ədədi nəticə ilə qovuşması riyazi harmoniyanın parlaq nümunəsidir. Təbiətin formalarında və mühəndis strukturlarda simmetriya axtardıqca bərabəryanlı üçbucağın sahə düsturu yeni rakurslardan özünü göstərir: kristal quruluşu modelləşdirərkən, dron eniş platformasını hesablarkən, hətta qrafik dizaynda simvol emblemi düzərkən. Riyaziyyatın zəngin arsenalı bu kiçik fiqur ətrafında seysraf kimi cəmlənir və hər bir düstur digəri ilə dialoq qurur. Beləliklə, bərabəryanlı üçbucaq sadəcə iki bərabər yanla məhdud olmayan, sonsuz analitik və estetik əlaqələrə açılan qızıl qapıdır; onu bilmək not açarını öyrənmək kimidir – arxasında bütöv musiqi dünyası gizlənir.
Ən Çox Verilən Suallar
Əgər baza və hündürlük məlumdursa, S = (b·h)/2 klassik düsturu ən sürətli yoldur. Hündürlüyü ayrıca ölçmək mümkün deyilsə, baza ilə yan kənar məlum olduqda Heron düsturu birbaşa hesablama imkanı verir. Kiçik konstruktiv layihələrdə iki kənarın ölçülməsi üçün lazer məsafəölçən kifayət edir. Beləliklə, praktiki sürət seçilən ölçü alətlərindən asılıdır.
Yan kənarların hər ikisi eyni, baza fərqli olmalıdır ki, üçbucaq bərabəryanlı olsun. Yanla baza qarışdırılmamalıdır, çünki yan kənarlar təpə bucağından çıxan hissələrdir, baza isə onların qarşısında yerləşən kənardır. Bütün üç kənar bərabər olarsa, bu artıq bərabəryanlı deyil, bərabəryanlıdan daha xüsusi – bərabəryanlı-hərtərəfli üçbucaqdır.
Hündürlük eyni zamanda median və bucaq bisektoru funksiyasını icra edir. Bundan əlavə, baza üzərində təpə nöqtəsindən endirilən hündürlük üçbucağı iki tamamilə eyni düzbucaqlıya bölür. Deməli, hündürlük kəsişməsində üç simmetriya oxu üst-üstə düşür, bu da hesablamanı sadələşdirir.
Bərabəryanlı üçbucaqda təpə bucağının sinusu bərabər yanların yaratdığı yüksək eninə sabit nisbətdə dəyişir. Təpə bucağı kiçikdirsə, sinθ kiçik, cosθ isə böyük olur. Sahəni sinusla hesabladıqda yan kənarın kvadratı ilə sinθ çarpanına üstünlük veririk, çünki bucaq və kənar birlikdə ölçüləndə nəticə daha dəqiq olur. Kosinus isə bazanı tapmaq üçün istifadə olunur.
Kartes koordinatlarında üç nöqtənin vektor koordinatlarını götürüb AB və AC vektorlarını hesablamaq, sonra vektor hasilinin modulunu iki yerə bölmək kifayətdir. Bu üsul ekrana baxış bucağından asılı olmayaraq doğru sahə verir. Blender, Unity kimi mühitlərdə hazır determinant funksiyası mövcuddur.
Çox vaxt dairəvi və ya sferik konstruksiyalarda, məsələn günəş panelinin qovşağını hesablarkən radius artıq məlum olur. Daxili radius sahənin sadə hesabına, xarici radius isə statik güc analizinədək vacib parametrlərə çevrilir. Belə hallarda radius düsturu hündürlük metodundan daha sürətli və ardıcıl nəticə verir.
Yan kənarlarla baza dəqiqliyini artırmaq üçün bir kənarı iki tərəfdən, yəni müxtəlif nöqtələrdən ölçüb orta qiymət götürmək məsləhətdir. Bundan başqa, Heron düsturunda bütün kənarlar kvadratik fərqə girdiyindən xətalar da kvadratla böyüyür; statistik sabitləşdirmə üçün Monte-Karlo üsulu ilə lazım olan dəqiqlikdə təxmini qiymət tapmaq mümkündür.
Qanad profillərinin hissə-hissə inteqrasiyasında bərabəryanlı bölmələr lift və süzülmə əmsalını səyfəsiz modelləşdirməyə imkan verir. Sahə düsturları yan basqıları və hava müqavimətini hesablayan diferensial tənliklərə sadə koordinat kimi daxil olur. Simmetriya qanad stabilizasiyasını və yük paylaşmasını optimallaşdırır.
Helioqrafiya gün işığı ilə kağızın kimyəvi təbəqəsinin yanmasını tələb edir, üçbucaq isə linzadan keçən işıq şüalarının düşmə bucağında ölçü moduludur. Bərabəryanlı kənarlar istənilən saatda kölgə sahəsinin sabit nisbətini qoruyur və nəticədə rəsmin tündlük dərəcəsi əvvəlcədən proqnozlaşdırılır.
Təpə bucağı çox kiçik olduqda sinθ təxminən θ radian olur və böyük kənar kvadratının kiçik sinusa vurulması sahə düsturunda xırda fərqləri böyük nəticə dəyişikliyinə çevirir. Buna həm də yuvarlaqlaşdırma xətası deyilir. Mühəndislər bu riski azaltmaq üçün əlavə köməkçi ölçü alətləri və çoxbucaqlı parçalanma metodu istifadə edirlər.