Riyaziyyatın əsas bölmələrindən olan silsilələr insan təfəkkürünün ardıcıllıq, nizam və proqressiya anlayışını riyazi dillə ifadə etməyə imkan verir. Silsilə, xüsusən də həndəsi silsilə, təkcə riyaziyyat dərslərində deyil, gündəlik həyatın bir çox sahələrində, texnologiyada, maliyyədə, hətta biologiyada təbiət qanunlarının, artım və azalmanın, dinamik proseslərin analizi üçün geniş istifadə olunur. Həndəsi silsilənin öyrənilməsi, həm analitik düşüncənin inkişafı, həm də real problemlərin həllində düzgün metod seçimi baxımından böyük əhəmiyyət kəsb edir. Bu anlayışın mənşəyi qədim Yunan riyaziyyatına qədər gedib çıxır və tarix boyu bir çox alimlər tərəfindən tədqiq olunub.
Həndəsi silsilənin fərqi ondadır ki, burada hər bir sonrakı element əvvəlkindən müəyyən sabit ədədə – “qəlib əmsalına” (mütənasiblik əmsalına) vurularaq alınır. Bu proqressiya modeli təkcə riyazi məsələ kimi yox, eyni zamanda bir çox təbii və sosial hadisələrin təhlilində universal alət rolunu oynayır.
Həndəsi silsilə anlayışı və əsas tərifi
Həndəsi silsilə – hər bir ədədi əvvəlkindən sabit ədədi (q) hasil almaqla əldə olunan ardıcıllığa deyilir. Riyazi dillə desək, belə bir silsilənin istənilən iki ardıcıl üzvü arasında aşağıdakı bərabərlik mövcuddur:
aₙ = a₁ × qⁿ⁻¹
Burada:
- aₙ – silsilənin n-ci üzvü
- a₁ – silsilənin birinci üzvü
- q – həndəsi silsilənin qəlib əmsalı (mütənasiblik əmsalı), q ≠ 0
- n – silsilənin ardıcıl sıra nömrəsi
Əgər qəlib əmsalı q > 1 olarsa, silsilə artan, 0 < q < 1 olarsa azalan, q < 0 olarsa isə dəyişkən işarəli olur.
Həndəsi silsilənin nümunələri və gündəlik həyatda rolu
Həndəsi silsilə həyatın bir çox sahəsində rast gəlinir:
| Sfera | Nümunə | İzah |
|---|---|---|
| Maliyyə | Bankda illik faizlə artan depozit | Əmanətin hər il əvvəlki məbləğin q dəfə artması |
| Biologiya | Bakteriyaların bölünməsi | Hər nəsildə bakteriyaların sayı 2 dəfə artır |
| Texnologiya | Radiodalğanın gücünün eksponensial azalması | Səs və ya işıq intensivliyinin hər mərhələdə eyni nisbətdə azalması |
| Riyaziyyat | 1, 2, 4, 8, 16… | Hər sonrakı üzv 2-yə vurulmaqla alınır |
| Fizika | Radioaktiv parçalanma, eksponensial çürümə | Atomların sayı hər mərhələdə müəyyən nisbətdə azalır |
Bu cədvəl həndəsi silsilənin nəzəriyyədən praktikaya keçidini və geniş tətbiq imkanlarını nümayiş etdirir.
Həndəsi silsilənin əsas xassələri və formulları
Həndəsi silsilənin ən əsas xüsusiyyətləri aşağıdakılardır:
- Hər bir üzv əvvəlki üzvün qəlib əmsalına vurulması ilə alınır:
aₙ = aₙ₋₁ × q - Silsilənin n-ci üzvü üçün ümumi düstur:
aₙ = a₁ × qⁿ⁻¹ - İlk n üzvün cəmi (Sₙ):
q ≠ 1 üçün:
Sₙ = a₁ × (qⁿ – 1) / (q – 1)
q = 1 üçün:
Sₙ = a₁ × n
Nümunə: 2, 6, 18, 54, … silsiləsində a₁ = 2, q = 3. Dördüncü üzv:
a₄ = 2 × 3³ = 2 × 27 = 54
İlk dörd üzvün cəmi:
S₄ = 2 × (3⁴ – 1) / (3 – 1) = 2 × (81 – 1) / 2 = 2 × 80 / 2 = 80
Həndəsi silsilənin növləri
Həndəsi silsilə aşağıdakı əsas növlərə bölünür:
- Artan həndəsi silsilə (q > 1): Hər bir üzv əvvəlkindən böyük olur.
- Azalan həndəsi silsilə (0 < q < 1): Hər bir üzv əvvəlkindən kiçik olur.
- Alternativ işarəli həndəsi silsilə (q < 0): Silsilə üzvləri bir müsbət, bir mənfi olur.
Bu fərqlər praktiki məsələlərin həllində və təhlildə əsas rol oynayır.
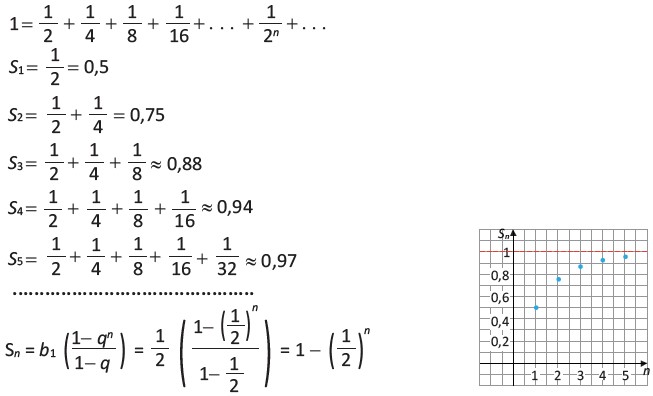
Həndəsi silsilənin sonsuzluğa yaxınlaşması və limit anlayışı
Əgər |q| < 1 olarsa, silsilə azalan və sonsuz üzvlərinin cəmi məhdud bir qiymətə yaxınlaşır. Sonsuz həndəsi silsilənin cəmi aşağıdakı kimi hesablanır:
S = a₁ / (1 – q), (|q| < 1 üçün)
Məsələn, a₁ = 1, q = 1/2 üçün:
S = 1 / (1 – 1/2) = 1 / (1/2) = 2
Bu, xüsusilə riyazi analizdə, fizika və iqtisadiyyatda mühüm əhəmiyyətə malikdir.
Həndəsi silsilənin gündəlik və elmi tətbiqləri
Həndəsi silsilənin tətbiqi imkanları olduqca genişdir. Bir neçə praktiki nümunə:
- Bank və maliyyə: Yığılan faizlər, kredit ödənişləri, investisiya gəlirliliyi.
- Ekologiya: Bioloji artım və azalma proseslərinin modelləşdirilməsi.
- Fizika və kimya: Maddələrin parçalanması, dinamik dəyişmə sürətinin hesablanması.
- İnformasiya texnologiyaları: Kompüter elmlərində məlumatların və gücün eksponensial artımı.
- Memarlıq və dizayn: Proqressiv artan ölçülər və modullar.
Bu tətbiqlər riyazi biliklərin həyatın müxtəlif sferalarında necə faydalı ola biləcəyini göstərir.
Həndəsi silsilə ilə arifmetik silsilə arasındakı fərqlər
Həndəsi silsilədə ardıcıl üzvlər bir sabit ədədlə vurulur, arifmetik silsilədə isə sabit ədəd əlavə olunur. Məsələn:
- Arifmetik: 3, 6, 9, 12, … (fərq = 3)
- Həndəsi: 3, 6, 12, 24, … (qəlib əmsalı = 2)
Bu fərq onların tətbiq sahələrində və riyazi analizdə istifadə üsullarında özünü göstərir.
Həndəsi silsilənin həndəsi orta ilə əlaqəsi
Həndəsi silsilənin ardıcıl iki üzvünün həndəsi ortası həmişə həmin silsilənin arasında yerləşir. Məsələn, a və aq üçün həndəsi orta: √(a × aq) = a√q. Bu, silsilənin strukturunda daxili nizamı təmin edir və bir çox məsələni asanlaşdırır.
Riyaziyyatda və elmdə həndəsi silsilənin əhəmiyyəti
Silsilələr, xüsusən həndəsi silsilə, eksponensial artım və azalma, təkrarlanan proseslər, fraktal quruluşlar, maliyyə modelləri, riyazi analiz və bir çox riyazi-fiziki qanunların əsasını təşkil edir. Onların öyrənilməsi analitik düşüncəni, məntiqi ardıcıllığı və modelləşdirmə bacarığını inkişaf etdirir.
Həndəsi silsilənin tapılması və tədrisi
Həndəsi silsilə məktəb proqramlarında əsas riyazi mövzulardan biri kimi öyrədilir. Məlumatlar cədvəl, qrafik, diaqram və konkret məsələlər üzərində təhlil olunur. Hesablama bacarıqları, təhlil və modelləşdirmə qabiliyyəti şagirdlərə aşılanır.
Cədvəldə həndəsi silsilənin əsas düsturları və nümunə hesablamalar göstərilib:
| Element | Formula | Nümunə |
|---|---|---|
| n-ci üzv | aₙ = a₁ × qⁿ⁻¹ | a₄ = 2 × 3³ = 54 |
| Cəm | Sₙ = a₁ × (qⁿ – 1) / (q – 1) | S₄ = 2 × (81-1)/2=80 |
| Sonsuz cəm | S = a₁ / (1 – q), | q |
Həndəsi silsilə riyaziyyatın ən əhəmiyyətli anlayışlarından biri olmaqla, real həyatın və elmin bir çox sahəsində tətbiq olunur. Onun strukturu, tətbiq formulları və modelləşdirmə üsulları riyazi düşüncəni inkişaf etdirir, analitik və praktiki problemlərin həllində böyük rol oynayır. Hər bir şagird, tələbə və mütəxəssis üçün həndəsi silsilənin məntiqini və tətbiqini dərindən anlamaq vacibdir.
Ən Çox Verilən Suallar
Həndəsi silsilə – hər bir üzvü əvvəlkindən müəyyən sabit ədədə (qəlib əmsalına) vurmaqla alınan ardıcıl ədədlər toplusudur.
n-ci üzv aₙ = a₁ × qⁿ⁻¹ düsturu ilə tapılır; burada a₁ – birinci üzv, q – qəlib əmsalı, n – sıra nömrəsidir.
Qəlib əmsalı (q) istənilən iki ardıcıl üzvün nisbətinə bərabərdir: q = aₙ/aₙ₋₁.
Sₙ = a₁ × (qⁿ – 1) / (q – 1) düsturu ilə hesablanır (q ≠ 1).
Əgər q > 1 olarsa, silsilə artan; 0 < q < 1 olarsa, azalan; q < 0 olarsa, işarələr alternativ olur.
Əgər |q| < 1 şərti ödənirsə, sonsuz silsilənin cəmi var və S = a₁ / (1-q) düsturu ilə tapılır.
Bank faizləri, əhali artımı, fiziki proseslər, investisiya və kredit modelləri, eksponensial dəyişənlərdə tətbiq edilir.
Arifmetik silsilədə ardıcıl üzvlər arasında sabit fərq var, həndəsi silsilədə isə ardıcıl üzvlər bir sabitə vurulur.
Əgər qəlib əmsalının modulu 1-dən kiçikdirsə (|q|<1), sonsuz həndəsi silsilənin cəmi məhdud olur.
Həndəsi silsilə məktəb proqramlarında əsas riyazi mövzulardan biridir, analitik və məntiqi düşüncənin inkişafına kömək edir.