Xətti funksiya riyaziyyatın əsas anlayışlarından biridir və müxtəlif elmi, texniki və gündəlik tətbiqlərdə geniş istifadə olunur. Xətti funksiya dəyişənlər arasında birbaşa və nisbət əlaqəsini göstərir, yəni dəyişənlərdən biri artdıqca digəri də mütənasib şəkildə artır və ya azalır. Bu funksiya anlayışı tələbələrin riyazi düşüncə bacarığını inkişaf etdirmək, fizika, iqtisadiyyat və mühəndislik sahələrində tətbiqi modellər qurmaq üçün vacibdir.
Xətti Funksiyanın Tərifi
Xətti funksiya, iki dəyişən xxx və yyy arasında birinci dərəcəli əlaqə yaradan funksiyadır. Ümumi formulu: y=kx+by = kx + by=kx+b
Burada kkk – meyl və ya istiqamət əmsalı, bbb isə başlanğıc nöqtəsi və ya interceptdir. kkk dəyəri funksiyanın artma və ya azalma xüsusiyyətini müəyyən edir:
- k>0k > 0k>0 – funksiya artandır
- k<0k < 0k<0 – funksiya azalandır
- k=0k = 0k=0 – funksiya sabitdir və üfüqi xətt kimi təmsil olunur
Bu tərif xətti funksiyanın əsas xüsusiyyətlərini və qrafik formasını müəyyən edir.
Xətti Funksiyanın Qrafiki
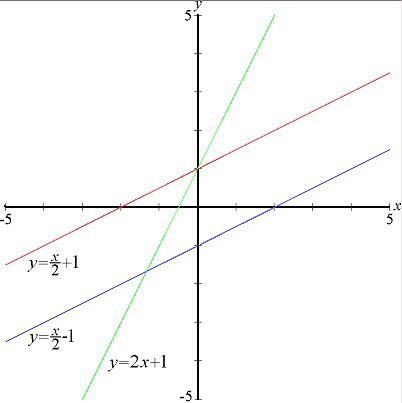
Xətti funksiyanın qrafiki mütləq bir düz xəttdir. Bu qrafikdə:
- bbb başlanğıc nöqtəsi olaraq y-oxunu kəsir
- kkk isə xəttin meylini göstərir
- Xəttin istiqaməti funksiyanın artım və ya azalma xüsusiyyətinə uyğun dəyişir
Məsələn, y=2x+3y = 2x + 3y=2x+3 funksiyasının qrafiki y-oxunu 333-də kəsir və xxx artdıqca yyy də ikiqat artır. Qrafik vizual olaraq funksiyanın davranışını təhlil etmək üçün mühüm vasitədir.
Xətti Funksiyanın Xüsusiyyətləri
Xətti funksiyanın əsas xüsusiyyətləri aşağıdakılardır:
- Düz xətt qrafiki – hər xətti funksiya düz xətt kimi qrafikdə əks olunur
- Müntəzəm dəyişiklik – dəyişən artdıqca funksiya da sabit nisbətdə dəyişir
- Interceptlər – qrafik y-oxunu bbb nöqtəsində, x-oxunu isə x=−b/kx = -b/kx=−b/k nöqtəsində kəsir
- Artma və azalma – meyl əmsalı kkk vasitəsilə müəyyən edilir
- Proqnoz və modelləşdirmə – xətti funksiya müxtəlif sahələrdə məlumatların proqnozlaşdırılması üçün istifadə olunur
Bu xüsusiyyətlər xətti funksiyanın həm nəzəri, həm də praktiki aspektlərini əhatə edir.
Xətti Funksiyanın Həlli və Hesablama Metodları
Xətti funksiyanın dəyərlərini hesablamaq üçün aşağıdakı üsullar tətbiq olunur:
- Əvəz etmə metodu – verilmiş xxx dəyərini funksiyaya qoyaraq yyy-nin tapılması
- Qrafik üsul – qrafik üzərində koordinatları oxuyaraq qiymətlərin müəyyənləşdirilməsi
- Cədvəl üsulu – müxtəlif xxx dəyərləri üçün yyy cədvəli hazırlanır
- Tərs funksiya – y=kx+by = kx + by=kx+b funksiyasından xxx dəyərini tapmaq üçün tərs əməliyyat aparılır: x=(y−b)/kx = (y-b)/kx=(y−b)/k
Bu üsullar tələbələr və mütəxəssislər üçün funksiyanın tətbiqini asanlaşdırır.
Xətti Funksiyanın Tətbiq Sahələri
Xətti funksiyalar çoxsaylı sahələrdə istifadə olunur:
- Fizika – hərəkət, sürət, gərginlik və temperatur dəyişikliklərinin modelləşdirilməsi
- İqtisadiyyat – gəlir, xərclər, təklif və tələb funksiyalarının təhlili
- Mühəndislik – elektrik dövrələri, material müqaviməti və yük paylanması hesablamaları
- Riyazi modelləşdirmə – müxtəlif təhlil və proqnozlarda xətti əlaqələrin istifadə olunması
Bu tətbiqlər xətti funksiyanın praktik əhəmiyyətini artırır.
Artım və Azalma Xüsusiyyətləri
Xətti funksiyada artım və azalma birbaşa meyl əmsalından asılıdır:
- k>0k > 0k>0 – funksiyanın artması, yəni xxx artdıqca yyy də artır
- k<0k < 0k<0 – funksiyanın azalması, yəni xxx artdıqca yyy azalır
- k=0k = 0k=0 – funksiyanın sabit qalması
Bu xüsusiyyətlər qrafik təhlil və real həyatda modelləşdirmə üçün mühümdür.
Qrafik və Analitik Təhlil
Xətti funksiyanın qrafiki ilə analitik təhlil birlikdə aparılır:
- Qrafik üsulu funksiyanın vizual təsvirini təmin edir
- Analitik üsul dəyərlərin dəqiqliyini təmin edir
- Hər iki üsul birlikdə tətbiq olunduqda nəticələr daha etibarlı olur
Bu yanaşma həm təhsil, həm də peşəkar sahələr üçün effektivdir.
Xətti Funksiyanın Qeyri-Müəyyən və Həll Növləri
Xətti funksiyanın xətti tənliklərlə bağlı qeyri-müəyyən və müəyyən halları mövcuddur:
- Unikal həll – funksiyanın bir konkret xətti və başlanğıc nöqtəsi
- Sonsuz həll – xətti funksiyanın qrafiki digər xəttlə üst-üstə düşdükdə
- Həllsiz hallar – xəttlər paralel olduqda və heç bir kəsişmə olmadıqda
Bu halların başa düşülməsi xətti funksiyanın analitik təhlilində vacibdir.
Təhsil və Tədrisdə Rolu
Xətti funksiya məktəb və universitet təhsilində əsas anlayışlardan biridir:
- Riyaziyyat dərslərində əsas anlayışlar öyrədilir
- Funksiya qrafiklərinin çəkilməsi və analitik hesablamalar tələbələrə analitik düşüncəni inkişaf etdirməyə kömək edir
- Problemlərin həlli və real həyatda tətbiqi bacarıqları formalaşdırılır
Xətti funksiyanın tədrisi tələbələrin riyazi savadını və analitik bacarıqlarını artırır.
Müasir Tətbiqlər və Rəqəmsal Platformalar
2025-ci il üçün xətti funksiyaların tətbiqi müasir texnologiyalarla genişlənir:
- Rəqəmsal tədris proqramları – interaktiv qrafiklər və vizual analiz
- Kompüter modelləşdirmə – xətti funksiyaların real həyatda proqnozlaşdırılması
- Tətbiqi proqramlar – iqtisadi və fiziki modellər üçün simulasiya
Bu inkişaf xətti funksiyanın həm təhsil, həm də tətbiqi sahələrdə əhəmiyyətini artırır.
Xətti funksiya riyaziyyatın və tətbiqi elmlərin əsas anlayışlarından biridir. Onun tərifi, qrafik təhlili, həll üsulları və tətbiqi sahələri tələbələr və mütəxəssislər üçün mühümdür. 2025-ci ildə rəqəmsal platformalar və müasir tədris metodları xətti funksiyanın öyrənilməsini və tətbiqini daha da səmərəli edəcək. Xətti funksiya həm nəzəri, həm də praktik baxımdan riyazi savadın və analitik düşüncənin əsasını təşkil edir.
Ən Çox Verilən Suallar
Xətti funksiya dəyişənlər arasında birinci dərəcəli və birbaşa nisbət əlaqəsini ifadə edən funksiyadır, y = kx + b formulu ilə göstərilir.
Xətti funksiyanın qrafiki mütləq düz xətt olur və meyl əmsalı k funksiyanın artım və azalma xüsusiyyətini müəyyən edir.
Meyl əmsalı k və intercept b xətti funksiyanın əsas elementləridir.
Meyl əmsalı k > 0 olduqda funksiya artır, k < 0 olduqda azalır, k = 0 olduqda isə sabit qalır.
Xətti funksiyanın qiymətlərini hesablamaq üçün əvəz etmə metodu və cədvəl üsulu istifadə olunur.
Xətti funksiyanı vizual olaraq təhlil etmək, qrafikdə intercept və meylini görmək üçün vacibdir.
Fizika, iqtisadiyyat, mühəndislik, riyazi modelləşdirmə və statistik analiz sahələrində tətbiq olunur.
Qrafik vizual təsvir verir, analitik üsul isə dəqiq hesablamaları təmin edir, birlikdə istifadə zamanı nəticələr daha etibarlıdır.
Unikal həll, sonsuz həll və həllsiz hallar mövcuddur.
Analitik düşüncəni inkişaf etdirmək, problemləri həll etmək və real həyatda tətbiq bacarıqlarını öyrətməkdir.